Question
A pendulum consists of a solid sphere suspended by a string from a fixed point P, as shown in Fig. 3.1.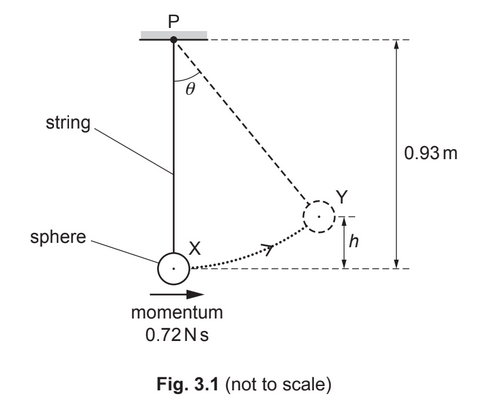
The sphere swings from side to side. At one instant the sphere is at its lowest position X, where it has kinetic energy 0.86J and momentum 0.72Ns in a horizontal direction. A short time later the sphere is at position Y, where it is momentarily stationary at a maximum vertical height h above position X.
The string has a fixed length and negligible weight. Air resistance is also negligible.
(a) On Fig. 3.1, draw a solid line to represent the displacement of the centre of the sphere at position Y from position X. [1]
(b) Show that the mass of the sphere is 0.30kg.
(c) Calculate height h.
h = …………………………………………….. m [2]
(d) The distance between point P and the centre of the sphere is 0.93m. When the sphere is at position Y, the string is at an angle θ to the vertical. Show that θ is 47°. [1]
(e) For the sphere at position Y, calculate the moment of its weight about point P.
moment = ………………………………………….. Nm [2]
(f) State and explain whether the sphere is in equilibrium when it is stationary at position Y.
……………………………………………………………………………………………………………………………
Answer/Explanation
Ans:
(a) solid straight line drawn between centre of sphere at X and at Y
(b) 
(c) (Δ)E = mg(Δ)h
h = 0.86 / (0.30 × 9.81)
= 0.29 m
(d) cos θ = (0.93 – 0.29) / 0.93 so θ = 47°
(e) 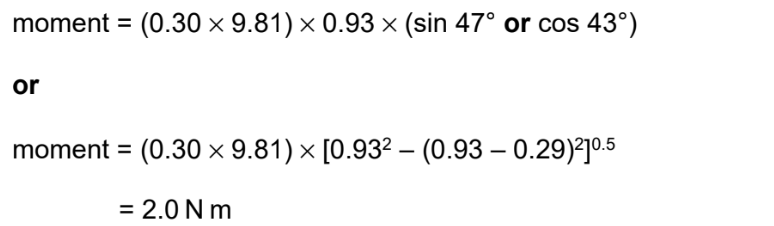
(f) there is a resultant force (acting on sphere)
or
there is a resultant moment (about P acting on pendulum)
(so) not in equilibrium
Question
(a) State two conditions for an object to be in equilibrium.
1. ……………………………………………………………………………………………………………………………..
2. ……………………………………………………………………………………………………………………………..
(b) A sphere of weight 2.4N is suspended by a wire from a fixed point P. A horizontal string is used to hold the sphere in equilibrium with the wire at an angle of 53° to the horizontal, as shown in Fig. 3.1.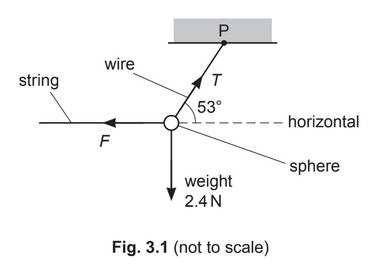
(i) Calculate:
1. the tension T in the wire
T = …………………………………………………… N
2. the force F exerted by the string on the sphere.
F = …………………………………………………… N
(ii) The wire has a circular cross-section of diameter 0.50mm. Determine the stress σ in the wire.
σ = ……………………………………………. Pa
(c) The string is disconnected from the sphere in (b). The sphere then swings from its initial rest position A, as illustrated in Fig. 3.2.
The sphere reaches maximum speed when it is at the bottom of the swing at position B. The distance between P and the centre of the sphere is 75cm.
Air resistance is negligible and energy losses at P are negligible.
(i) Show that the vertical distance h between A and B is 15cm.
(ii) Calculate the change in gravitational potential energy of the sphere as it moves from A to B.
change in gravitational potential energy = ……………………………………………… J
(iii) Use your answer in (c)(ii) to determine the speed of the sphere at B.
Show your working.
speed = ………………………………………… \(ms^{–1}\)
Answer/Explanation
Answer:
(a) resultant force (in any direction) is zero
resultant torque/moment (about any point) is zero
(b) (i) 1. T sin 53° = 2.4
T = 3.0 N
2. F =
T cos 53° or \(F^2 = T^2 – 2.4^2\)
F = 1.8 N
(ii) σ = T / A or σ = F / A
\(A = π d^2 / 4 or A = πr^2\)
\(σ = 3.0 × 4 / [π × (0.50 × 10^{–3})^2]\)
= \(1.5 × 10^7\) Pa
(c) (i) h = 75 – 75 sin 53° = 15 cm
(ii) (Δ)E = mg(Δ)h or ( Δ)E = W(Δ)h
(Δ)E = 2.4 × 15 × \(10^–2\)
= 0.36 J
(iii) \(E = 1/2 mv^2\)
\(0.36 – 1/2 \times (2.4/ 9.81) \times v^2\)
\(v = 1.7 ms^{-1}\)
