Question
(a) State two conditions for an object to be in equilibrium.
1. ……………………………………………………………………………………………………………………………..
2. ……………………………………………………………………………………………………………………………..
(b) A sphere of weight 2.4N is suspended by a wire from a fixed point P. A horizontal string is used to hold the sphere in equilibrium with the wire at an angle of 53° to the horizontal, as shown in Fig. 3.1.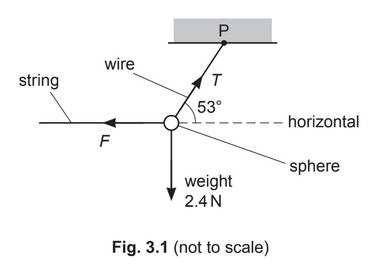
(i) Calculate:
1. the tension T in the wire
T = …………………………………………………… N
2. the force F exerted by the string on the sphere.
F = …………………………………………………… N
(ii) The wire has a circular cross-section of diameter 0.50mm. Determine the stress σ in the wire.
σ = ……………………………………………. Pa
(c) The string is disconnected from the sphere in (b). The sphere then swings from its initial rest position A, as illustrated in Fig. 3.2.
The sphere reaches maximum speed when it is at the bottom of the swing at position B. The distance between P and the centre of the sphere is 75cm.
Air resistance is negligible and energy losses at P are negligible.
(i) Show that the vertical distance h between A and B is 15cm.
(ii) Calculate the change in gravitational potential energy of the sphere as it moves from A to B.
change in gravitational potential energy = ……………………………………………… J
(iii) Use your answer in (c)(ii) to determine the speed of the sphere at B.
Show your working.
speed = ………………………………………… \(ms^{–1}\)
Answer/Explanation
Answer:
(a) resultant force (in any direction) is zero
resultant torque/moment (about any point) is zero
(b) (i) 1. T sin 53° = 2.4
T = 3.0 N
2. F =
T cos 53° or \(F^2 = T^2 – 2.4^2\)
F = 1.8 N
(ii) σ = T / A or σ = F / A
\(A = π d^2 / 4 or A = πr^2\)
\(σ = 3.0 × 4 / [π × (0.50 × 10^{–3})^2]\)
= \(1.5 × 10^7\) Pa
(c) (i) h = 75 – 75 sin 53° = 15 cm
(ii) (Δ)E = mg(Δ)h or ( Δ)E = W(Δ)h
(Δ)E = 2.4 × 15 × \(10^–2\)
= 0.36 J
(iii) \(E = 1/2 mv^2\)
\(0.36 – 1/2 \times (2.4/ 9.81) \times v^2\)
\(v = 1.7 ms^{-1}\)
Question
(a) Define:
(i) displacement
(ii) acceleration.
(b) A man wearing a wingsuit glides through the air with a constant velocity of \(47ms^{–1}\) at an angle of \(24\)° to the horizontal. The path of the man is shown in Fig. \(2.1\).
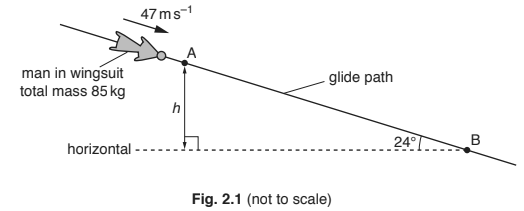
The total mass of the man and the wingsuit is \(85\) kg. The man takes a time of \(2.8\) minutes to glide from point A to point B.
(i) With reference to the motion of the man, state and explain whether he is in equilibrium.
(ii) Show that the difference in height h between points A and B is \(3200\)m.
(iii) For the movement of the man from A to B, determine:
1. the decrease in gravitational potential energy
2. the magnitude of the force on the man due to air resistance.
(iv) The pressure of the still air at A is \(63\) kPa and at B is \(92\) kPa. Assume the density of the air is constant between A and B.
Determine the density of the air between A and B.
Answer/Explanation
Ans:
(a) (i) distance in a specified direction (from a point)
(ii) change in velocity / time (taken)
(b) (i) constant velocity so no resultant force
no resultant force so in equilibrium
(ii) (difference in height =) \(47 \times 2.8 \times 60 \times \sin 24° = 3200 m\)
(iii) 1. \((\Delta )E = mg(\Delta )h\)
= \(85\times 9.81\times 3200\)
= \(2.7\times 10^{6}\)J
2. In terms of energy:
work done = \(2.7\times 10^{6}\)J
force = \(2.7\times 10^{6}/ (47\times 2.8 \times 60)\)
= \(340\) N
In terms of forces:
component of weight along path = force due to air resistance
force = \(85\times 9.81 \times \sin 24°\)
= \(340\) N
(iv) \( (\Delta )p = \rho g(\Delta )h\)
\((92 -63)\times 10^{3} = \rho \times 9.81\times 3200\)
\(\rho = 0.92 kg\, m^{-3}\)
