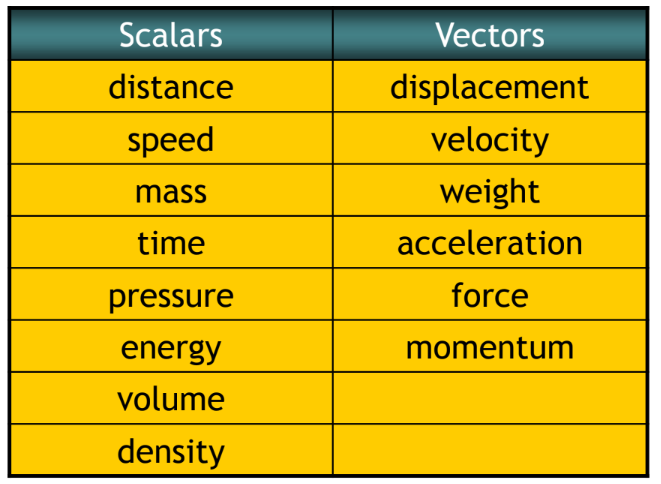
Scalars and Vectors
• Examples of scalars and vectors
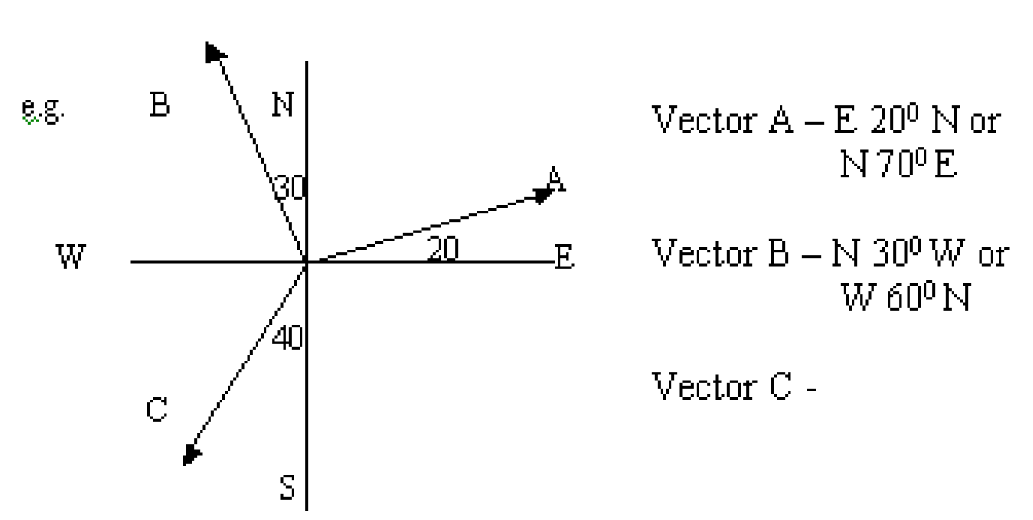
Direction of vector
Scalars and Vectors
Adding/Subtracting Vectors using Graphical Method
• Parallel vectors can be added arithmetically
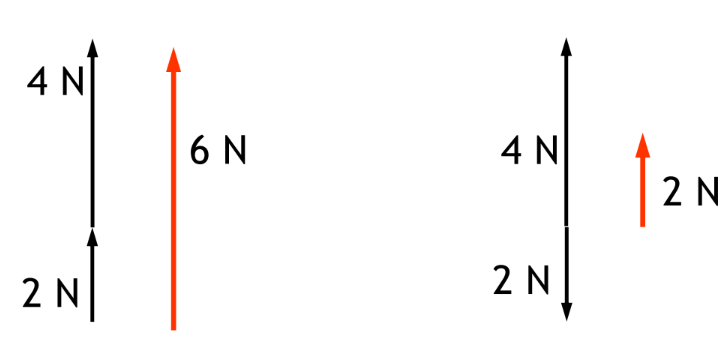
Scalars and Vectors
Adding Vectors using Graphical Method
• Non-parallel vectors are added by graphical means using the parallelogram law
– Vectors can be represented graphically by arrows

– The length of the arrow represents the magnitude of the vector
– The direction of the arrow represents the direction of the vector
– The magnitude and direction of the resultant vector can be found using an accurate scale drawing
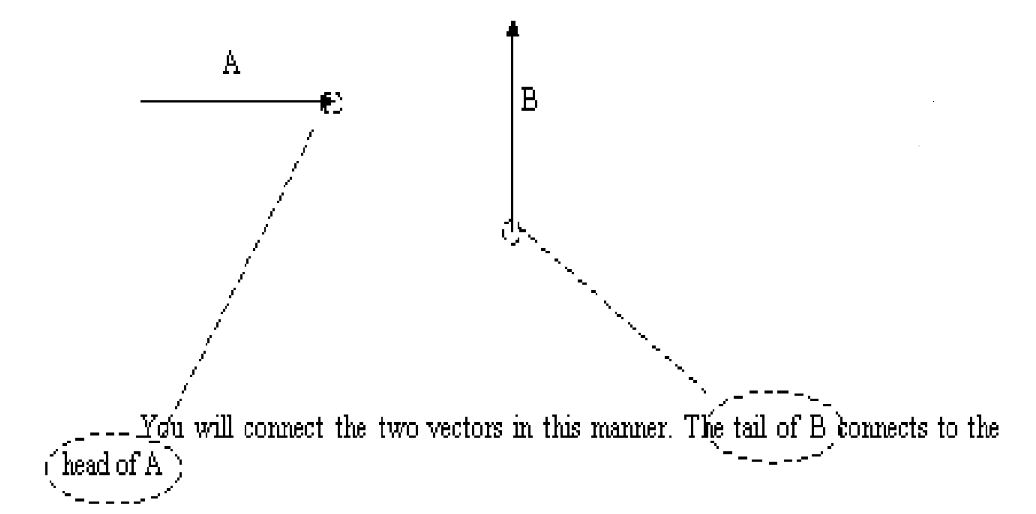
Vector addition
(a) Drawing method
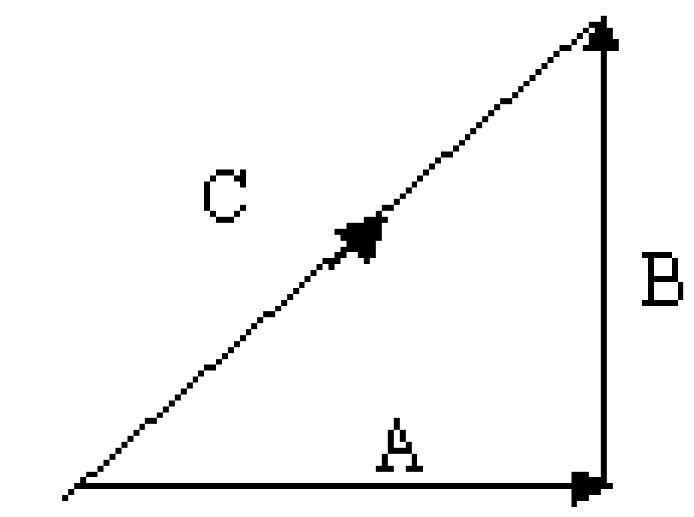
Eg. Below are two vectors A and $B$.
What will be the result of adding them up? The resultant vector is the one that you get when you add two or more vectors together. It is a single vector that has the sarme effect as all the others put together.
Let’s describe the result as $\mathrm{C}$. So $C=A+B$
Vector operation
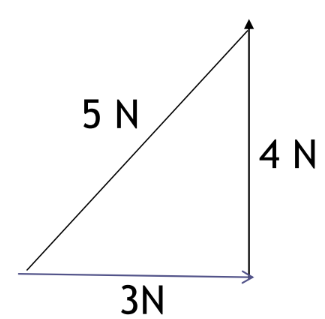
- Vector problem must be solved vectorically unlike scalar quantity.
- E.g. $3 N+4 N=5 N$
Addition using drawing method
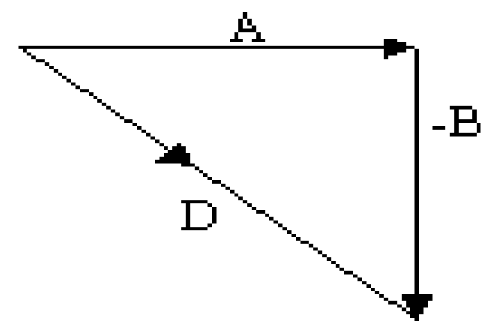
Subtraction using drawing method
• if D = A – B
Scalars and Vectors
- The parallelogram law of vector addition states that if two vectors acting at a point are represented by the sides of a parallelogram drawn from that point, their resultant is represented by the diagonal which passes through that point of the parallelogram
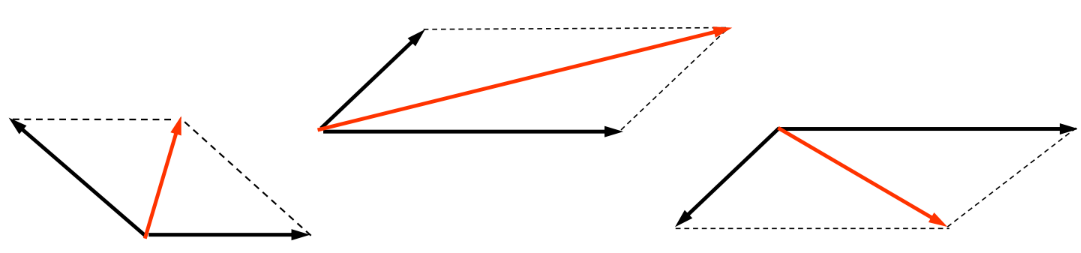
Coplanar vectors
• When 3 or more vectors need to be added, the same principles apply, provided the vectors are all on the same plane i.e. coplanar
• To subtract 2 vectors, reverse the direction i.e. change the sign of the vector to be subtracted, and add
Change in a Vector
Case 1
• If an object changes it’s direction but not speed, then velocity vector will only change its direction but not magnitude.
Case 2
• If an object changes it’s direction and also speed, vector will change its direction as well as magnitude. So the change in the vector would be final minus initial.
Components of a Vector
- Any vector directed in two dimensions can be thought of as having an influence in two different directions. That is, it can be thought of as having two parts. Each part of a vector is known as a component.
- $\downarrow 2 \mathrm{~N}+\downarrow 4 \mathrm{~N}=\downarrow 6 \mathrm{~N}(2 \mathrm{~N}$ and $4 \mathrm{~N}$ are the components of $6 \mathrm{~N})$
- The components of a vector depict the influence of that vector in a given direction. The combined influence of the two components is equivalent to the influence of the single vector. The single vector could be replaced by the two components.
Components of a Vector
- Any vector can be thought of as having two different components. The component of a single vector describes the influence of that vector in a given direction.
$\cdot \overrightarrow{3 \mathrm{~N}}+4 \overrightarrow{\mathrm{N}}=\overrightarrow{7 \mathrm{~N}} \overrightarrow{(3 \mathrm{~N}}$ and $\overrightarrow{4 \mathrm{~N}}$ are the components of $\overrightarrow{7 \mathrm{~N}})$
Resolution of vectors
- Resolving vectors into two perpendicular components
A vector can be broken down into components, which are perpendicular to each other, so that the vector sum of these two components, is equal to the original vector.
Splitting a vector into two components is called resolving the vector. It is the reverse of using Pythagoras’ theorem to add two perpendicular vectors, and so adding the two components will give you the original vector.
Resolution of vectors
- Resolving vectors into two perpendicular components
- Resolving a vector requires some simple trigonometry. In the diagram, the vector to be resolved is the force, $\mathrm{F}$ for angle A;
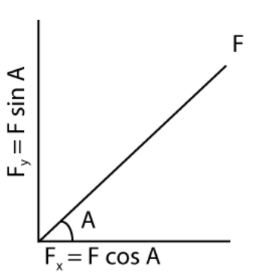
the horizontal component of $\mathrm{F}: F_x=F \cos A$
the vertical component of $\mathrm{F}: F_y=F \sin A$
Note that the two components do not have to be horizontal and vertical. The angle can be changed to any required direction, and both components will still be perpendicular to each other
Resolution of vectors
• Resolving vectors into two perpendicular components
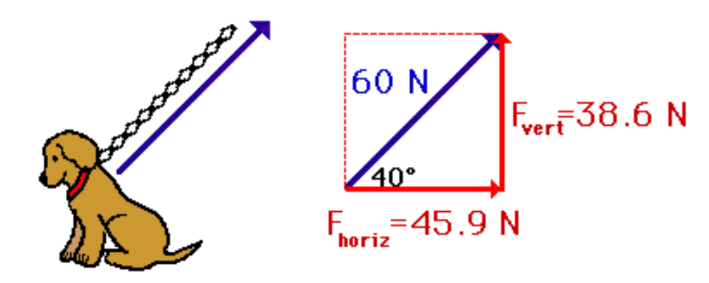
$\begin{array}{cc}\sin 40^{\circ}=\frac{F_{\text {vert }}}{60 \mathrm{~N}} & \cos 40^{\circ}=\frac{\mathrm{F}_{\text {horiz }}}{60 \mathrm{~N}} \\ \mathrm{~F}_{\text {vert }}=60 \mathrm{~N} \times \sin 40^{\circ} & \mathrm{F}_{\text {horiz }}=60 \mathrm{~N} \times \cos 40^{\circ} \\ \mathrm{F}_{\text {vert }}=38.6 \mathrm{~N} & \mathrm{~F}_{\text {horiz }}=45.9 \mathrm{~N}\end{array}$
In short…
•Vectors addition and subtraction can be performed using diagram method or the resolve and recombine method
Key Concept
1. Scalar quantities are quantities that only have magnitudes
2. Vector quantities are quantities that have both magnitude and direction
3. Parallel vectors can be added arithmetically
4. Non-parallel vectors are added by graphical means using the parallelogram law.
5. Vectors addition and subtraction can be performed using diagram method or the resolve and recombine method
