Potential Divider
The potential divider circuit (fig. ) is one of the most useful circuits. The potential divider arrangement can be used to divide the input voltage $\left(V_s\right)$ in the ratio that we want. The circuit diagram for a potential divider arrangement is shown below:-
For a potential divider the current through each resistor is the same (why?they are in series,hence). The.
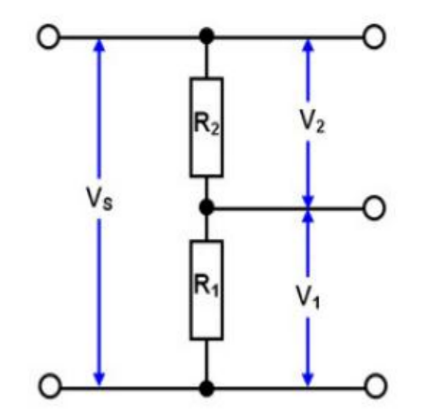
Figure $\therefore$ A potential Divider circuit
current in the circuit can be found by using the Ohms law and remembering that the total resistance in the circuit is $R_1+R_2$ we get
$
I=\frac{V_s}{R_1+R_2}
$
the voltage across the resistor $R_1$ is given by:-
$
V_1=I R_1
$
using (9) we get
$
V_1=I R_1=\frac{V_s R_1}{R_1+R_2}
$
Similarly ,the voltage across the resistor $R_2$ is given by:-
$
V_2=I R_2
$
using (9) we get
$
V_2=I R_2=\frac{V_s R_2}{R_1+R_2}
$
The ratio $V_1$ to $V_2$ can be found as:
$
\frac{V_1}{V_2}=\frac{R_1}{R_2}
$
Application of Potential Divider circuits
Temperature Sensor
A common example of a sensing system is a temperature sensor in a thermostat, which uses a thermistor(A thermistor is a kind of resistor whose resistance decreases as the temperature increases-it is generally made of semiconductors). The thermistor is then used in a potential divider, as in the diagram in fig.8. In this diagram, the potential difference is divided between the resistor and the thermistor. As the temperature rises, the resistance of the thermistor decreases, so the potential difference across it decreases. This means that potential difference across the resistor increases as temperature increases. This is why the voltage is measured across the resistor, not the thermistor. As the source voltage and $R$ are known using the graph below fig. 9 the temperature can be found.
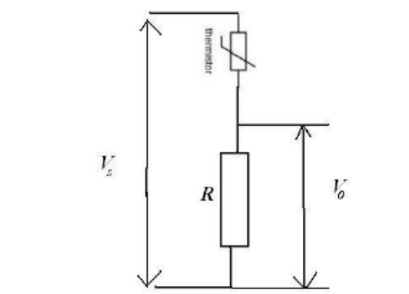
Figure 8: Thermistor as a temperature sensor
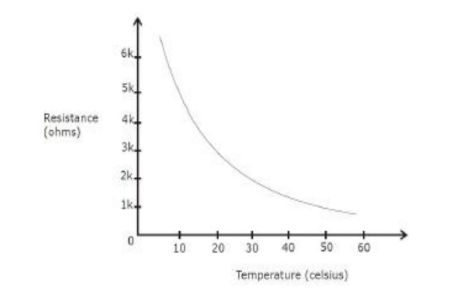
Figure 9: Temperature Vs resistance for a thermistor
Application of Potential Divider circuits
Light $D$ ependent $R$ esistors:Light-dependent resistors ( $L D R s$ ) have a resistance which changes in response to changes in light levels, as detected by a photo-sensitive plate on the resistor. Most LDRs have a negative light coefficient – meaning that their resistance falls as the amount of light falling on them increases. LDRs are used in light-detection circuits as shown in the figure below using the same technique as in the measurement of temperature the intensity of light can be measured with the circuit shown below .
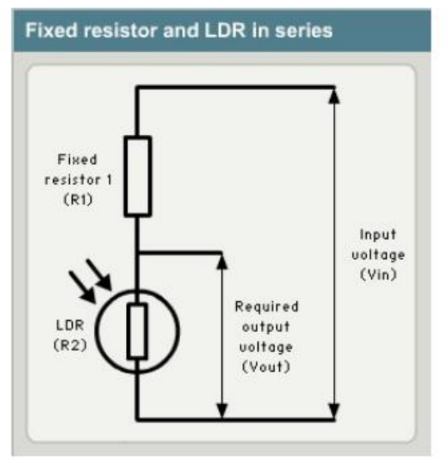
Potentiometer
A variable voltage-divider(potentiometer):A variable voltage divider is another form of the potential divider arrangement it is also called the potentiometer.Consider a long piece of high resistance wire $\mathrm{AB}$ connected to a battery as shown below:-
Between $\mathrm{A}$ and $\mathrm{J}$ a voltmeter is connected. The point $\mathrm{J}$ is a movable contact as the point $\mathrm{j}$ is moved
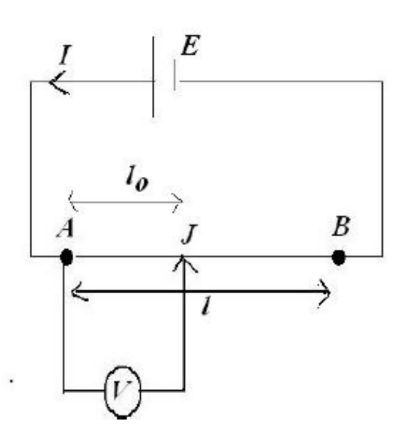
Figure 11: A variable voltage potential divider
Potentiometer (continued from previous slide)
the potential drop increases, hence by varying the length of AJ the potential can be varied.Let $\rho$ be the resistivity of the wire $\mathrm{AB}$ and let $E$ be $E m f$ of the battery,let $l_o$ be the length of wire AJ and let $l$ be the length AB then
$
E=I R=I \frac{\rho l}{A}
$
The drop $V$ across the length $\mathrm{AJ}$ whose resistance is $R_o$ is given by
$
V=I R_o=I \frac{\rho l_o}{A}
$
Dividing the above two equations we get
$
\frac{V}{E}=\frac{l_o}{l}
$
Potentiometer and its application Principle of Potentiometer
POTENTIOMETER:
Construction: The potentiometer consists of a long uniform wire usually made of manganin or constantan (high Resistivity low temp coeff of resistance). The ends of the wire are connected to binding screws A and B. A meter scale is fixed on the board .The potentiometer has jockey J with the help of which contact can be made with the potentiometer wire.
Principle: The fall of potential across any portion of the wire is directly proportional to the length of that portion, if the area of cross section is uniform and the current constant. If $\mathrm{I}$ is the constant current through the potentiometer wire and if $\mathrm{R}$ is the resistance between the wire between $\mathrm{A}$ and $\mathrm{J}$ Then
$
\begin{gathered}
V=I R \\
V=I \frac{\rho}{A} l
\end{gathered}
$
Note: This equation is going to be used for next application.
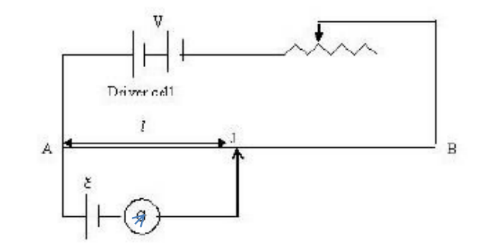
$
V=\phi l
$
where $\phi=I \frac{\rho}{A}$, and $\phi$ is called the potential gradient.
Hence the potential drop across the length of the potentiometer wire is directly proportional to the length. This is the principle of the potentiometer.
Note: The above equation is used for next application.
Comparison of EMF: The potentiometer can used to compare the emf of two cells with the help of the circuit diagram shown below. Let the emf’s of the cells to be compared be $\epsilon_1$ and $\epsilon_2$ let the driver cell potential be $\mathrm{V}$. The cells are connected to the potentiometer through a two way key. First the key
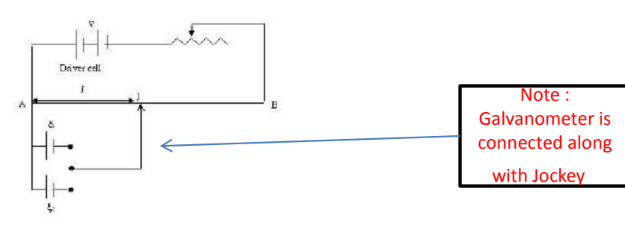
put in the two way key such that the cell with emf $\epsilon_1$ is connected to the circuit.The jockey(movable contact) is moved along the wire till at a point there is no deflection in the galvanometer, at a distance $l_1$ from $A$.
The EMF of the cell is proportional to the balancing length
$
\epsilon_1=\phi l_1
$
similarly when the second cell is connected
$
\epsilon_2=\phi l_2
$
dividing the equations
$
\frac{\epsilon_1}{\epsilon_2}=\frac{l_1}{l_2}
$
Note:(i)The Driver cell potential should always be greater than the potential of the cells whose emf’s are compared.(ii)If one cells emf is accurately known the other cells emf can be determined.
