CIE AS/A Level Physics 12.2 Centripetal acceleration Study Notes- 2025-2027 Syllabus
CIE AS/A Level Physics 12.2 Centripetal acceleration Study Notes – New Syllabus
CIE AS/A Level Physics 12.2 Centripetal acceleration Study Notes at IITian Academy focus on specific topic and type of questions asked in actual exam. Study Notes focus on AS/A Level Physics latest syllabus with Candidates should be able to:
- understand that a force of constant magnitude that is always perpendicular to the direction of motion causes centripetal acceleration
- understand that centripetal acceleration causes circular motion with a constant angular speed
- recall and use a = rω2 and a = v2 / r
- recall and use F = mrω2 and F = mv2 / r
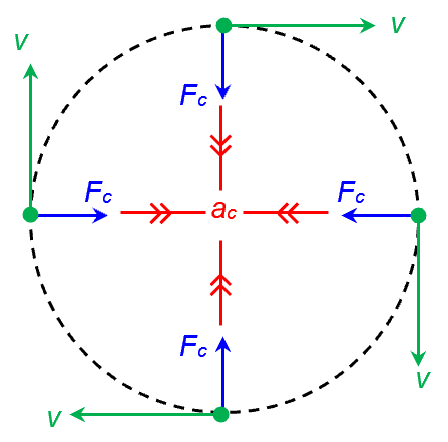
Centripetal Force and Perpendicular Acceleration
When an object moves in a circle at constant speed, the direction of its velocity continually changes. This change in direction means the object is accelerating, even though its speed remains constant.
Definition:
A force of constant magnitude that is always perpendicular to the direction of motion provides the centripetal acceleration that keeps an object moving in a circular path.
Expression for Centripetal Acceleration:
\( \mathrm{a_c = \dfrac{v^2}{r} = r\omega^2} \)
- \( \mathrm{a_c} \): centripetal acceleration (m/s²)
- \( \mathrm{v} \): linear (tangential) speed (m/s)
- \( \mathrm{r} \): radius of circular path (m)
- \( \mathrm{\omega} \): angular speed (rad/s)
Direction of Acceleration and Force:
- The acceleration and the force are directed towards the centre of the circle.
- The velocity of the object is always tangential to the circle, hence perpendicular to the force.
Key Idea:
A perpendicular force of constant magnitude changes only the direction of velocity, not its magnitude, thus maintaining uniform circular motion.
Example
A small stone of mass \( \mathrm{0.2 \ kg} \) is whirled in a horizontal circle of radius \( \mathrm{0.5 \ m} \) at a constant speed of \( \mathrm{4.0 \ m/s.} \) Calculate the centripetal acceleration acting on the stone.
▶️ Answer / Explanation
Using \( \mathrm{a_c = \dfrac{v^2}{r}} \):
\( \mathrm{a_c = \dfrac{4.0^2}{0.5} = \dfrac{16}{0.5} = 32 \ m/s^2.} \)
Therefore, the centripetal acceleration is \( \mathrm{32 \ m/s^2.} \)
Interpretation: The stone’s velocity constantly changes direction under a perpendicular force, producing circular motion.
Example
A car of mass \( \mathrm{1200 \ kg} \) travels around a level circular bend of radius \( \mathrm{50 \ m} \) at a constant speed of \( \mathrm{20 \ m/s.} \) The frictional force between the tires and road provides the centripetal force. Determine:
- (a) the centripetal acceleration,
- (b) the frictional force acting on the car.
▶️ Answer / Explanation
(a) Using \( \mathrm{a_c = \dfrac{v^2}{r}} \):
\( \mathrm{a_c = \dfrac{20^2}{50} = \dfrac{400}{50} = 8.0 \ m/s^2.} \)
(b) Centripetal force \( \mathrm{F_c = m a_c = 1200 \times 8.0 = 9600 \ N.} \)
Therefore:
- Centripetal acceleration = \( \mathrm{8.0 \ m/s^2} \)
- Frictional (centripetal) force = \( \mathrm{9600 \ N} \)
Interpretation: The force of friction acts perpendicular to the car’s velocity, providing the inward acceleration that changes its direction while keeping the speed constant.
Centripetal Acceleration and Constant Angular Speed
If a body moves in a circle under the influence of a constant perpendicular (centripetal) force, its speed remains constant but its direction changes continuously. This results in constant angular speed \( \mathrm{\omega} \).
Relationship between Linear and Angular Quantities:
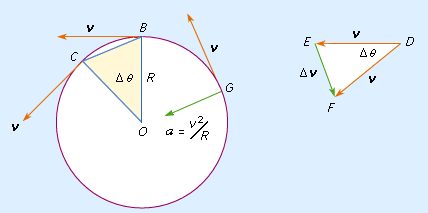
\( \mathrm{a_c = r\omega^2} \ \ \text{and} \ \ v = r\omega. \)
Explanation:
- The direction of motion changes continuously due to centripetal acceleration directed toward the centre.
- Since the magnitude of velocity remains constant, so does the angular speed \( \mathrm{\omega.} \)
- Hence, the motion is called uniform circular motion the object moves around the circle at constant speed but continuously changes direction.
Key Idea:
Centripetal acceleration maintains circular motion at constant angular speed, ensuring uniform motion without tangential acceleration.
Example
A ball moves in a horizontal circle of radius \( \mathrm{0.8 \ m} \) at a constant speed of \( \mathrm{3.0 \ m/s.} \) Find its angular speed and centripetal acceleration.
▶️ Answer / Explanation
Using \( \mathrm{\omega = \dfrac{v}{r}} \):
\( \mathrm{\omega = \dfrac{3.0}{0.8} = 3.75 \ rad/s.} \)
Now, \( \mathrm{a_c = r\omega^2 = 0.8 \times 3.75^2 = 11.25 \ m/s^2.} \)
Hence:
- Angular speed = \( \mathrm{3.75 \ rad/s} \)
- Centripetal acceleration = \( \mathrm{11.25 \ m/s^2} \)
Interpretation: Although the ball’s speed is constant, its velocity direction changes due to centripetal acceleration directed towards the centre.
Example
A satellite orbits Earth in a circular path of radius \( \mathrm{7.0 \times 10^6 \ m.} \) It completes one revolution every \( \mathrm{5800 \ s.} \) Determine:
- (a) its angular speed,
- (b) its linear speed,
- (c) its centripetal acceleration.
▶️ Answer / Explanation
(a) Using \( \mathrm{\omega = \dfrac{2\pi}{T}} \):
\( \mathrm{\omega = \dfrac{2\pi}{5800} = 1.08 \times 10^{-3} \ rad/s.} \)
(b) Linear speed \( \mathrm{v = r\omega = 7.0 \times 10^6 \times 1.08 \times 10^{-3} = 7.56 \times 10^3 \ m/s.} \)
(c) Centripetal acceleration \( \mathrm{a_c = r\omega^2 = 7.0 \times 10^6 \times (1.08 \times 10^{-3})^2 = 8.2 \ m/s^2.} \)
Hence:
- \( \mathrm{\omega = 1.08 \times 10^{-3} \ rad/s} \)
- \( \mathrm{v = 7.56 \times 10^3 \ m/s} \)
- \( \mathrm{a_c = 8.2 \ m/s^2} \)
Interpretation: The satellite’s constant angular speed ensures it remains in stable orbit — its direction changes continuously due to the gravitational centripetal force acting towards Earth’s centre.
Centripetal Acceleration — Formulas and Use
When an object moves in a circle at a constant speed, its direction of velocity continuously changes. This change in direction produces an acceleration directed towards the centre of the circle — called the centripetal acceleration.
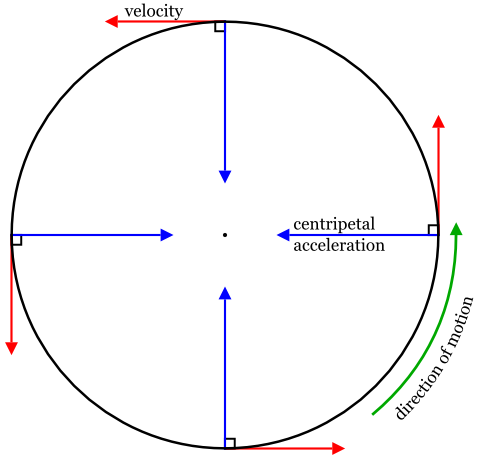
Formulas for Centripetal Acceleration:
\( \mathrm{a = \dfrac{v^2}{r}} \ \text{or} \ \mathrm{a = r\omega^2} \)
- \( \mathrm{a} \): centripetal acceleration (m/s²)
- \( \mathrm{v} \): linear or tangential speed (m/s)
- \( \mathrm{r} \): radius of circular path (m)
- \( \mathrm{\omega} \): angular speed (rad/s)
Relationship Between the Two Expressions:
Since \( \mathrm{v = r\omega} \), substituting gives \( \mathrm{a = \dfrac{(r\omega)^2}{r} = r\omega^2.} \)
Example
A stone is tied to a string of length \( \mathrm{1.2 \ m} \) and whirled in a horizontal circle at a speed of \( \mathrm{6.0 \ m/s.} \) Find the centripetal acceleration.
▶️ Answer / Explanation
Using \( \mathrm{a = \dfrac{v^2}{r}} \):
\( \mathrm{a = \dfrac{6.0^2}{1.2} = \dfrac{36}{1.2} = 30 \ m/s^2.} \)
Hence, the centripetal acceleration is \( \mathrm{30 \ m/s^2.} \)
Interpretation: The acceleration acts inward, keeping the stone in circular motion while the speed remains constant.
Example
A 2.0 kg object moves in a circular path of radius \( \mathrm{0.5 \ m.} \) If it completes 8 revolutions every second, calculate:
- (a) its angular speed,
- (b) its centripetal acceleration.
▶️ Answer / Explanation
(a) \( \mathrm{\omega = 2\pi f = 2\pi \times 8 = 50.27 \ rad/s.} \)
(b) Using \( \mathrm{a = r\omega^2:} \)
\( \mathrm{a = 0.5 \times (50.27)^2 = 0.5 \times 2527 = 1263.5 \ m/s^2.} \)
Hence: \( \mathrm{a = 1.26 \times 10^3 \ m/s^2.} \)
Interpretation: Even with a constant speed, the large angular speed produces a very high inward acceleration — typical for fast-rotating systems such as motors or turbines.
Centripetal Force — Formulas and Use
The centripetal force is the resultant force that acts towards the centre of a circular path, providing the necessary inward acceleration to keep an object moving in a circle.
![]()
Formulas for Centripetal Force:
\( \mathrm{F = \dfrac{mv^2}{r}} \ \text{or} \ \mathrm{F = mr\omega^2} \)
- \( \mathrm{F} \): centripetal force (N)
- \( \mathrm{m} \): mass of the object (kg)
- \( \mathrm{v} \): linear speed (m/s)
- \( \mathrm{r} \): radius of circle (m)
- \( \mathrm{\omega} \): angular speed (rad/s)
Direction: Always directed towards the centre of the circular path (the same as centripetal acceleration).
Relationship Between Acceleration and Force:
\( \mathrm{F = ma = m\dfrac{v^2}{r} = mr\omega^2.} \)
Example
A 0.5 kg ball is whirled in a circle of radius \( \mathrm{1.0 \ m} \) with a constant speed of \( \mathrm{4.0 \ m/s.} \) Calculate the centripetal force acting on it.
▶️ Answer / Explanation
Using \( \mathrm{F = \dfrac{mv^2}{r}} \):
\( \mathrm{F = \dfrac{0.5 \times 4.0^2}{1.0} = \dfrac{0.5 \times 16}{1.0} = 8.0 \ N.} \)
Hence: The tension in the string (centripetal force) is \( \mathrm{8.0 \ N.} \)
Interpretation: The force acts inward, perpendicular to the ball’s velocity, maintaining uniform circular motion.
Example
A 1000 kg car travels around a curve of radius \( \mathrm{80 \ m} \) at a speed of \( \mathrm{25 \ m/s.} \)
- (a) Calculate the required centripetal force.
- (b) Determine the minimum coefficient of friction between the tires and the road required to prevent the car from skidding.
▶️ Answer / Explanation
(a) Using \( \mathrm{F = \dfrac{mv^2}{r}} \):
\( \mathrm{F = \dfrac{1000 \times 25^2}{80} = \dfrac{1000 \times 625}{80} = 7.81 \times 10^3 \ N.} \)
(b) Maximum frictional force \( \mathrm{F_f = \mu mg.} \)
At the limit of skidding, \( \mathrm{F_f = F_c.} \)
\( \mathrm{\mu = \dfrac{F_c}{mg} = \dfrac{7.81 \times 10^3}{1000 \times 9.81} = 0.80.} \)
Hence:
- Centripetal force = \( \mathrm{7.8 \times 10^3 \ N.} \)
- Coefficient of friction = \( \mathrm{0.80.} \)
Interpretation: The frictional force must be at least 80% of the car’s weight to provide sufficient inward force for circular motion without skidding.
