Defining Gravitational Field
- There is a force of attraction between all masses
- This force is known as the ‘force due to gravity’ or the weight
- The Earth’s gravitational field is responsible for the weight of all objects on Earth
- A gravitational field is defined as:
- A region of space where a mass experiences a force due to the gravitational attraction of another mass
- The direction of the gravitational field is always towards the centre of the mass
- Gravitational forces cannot be repulsive
- The strength of this gravitational field $(g)$ at a point is the force $\left(F_g\right)$ per unit mass $(m)$ of an object at that point:
$
\mathrm{g}=\frac{F_g}{m}
$
- Where:
- $\mathrm{g}=$ gravitational field strength $\left(\mathrm{N} \mathrm{kg}^{-1}\right)$
- $F_g=$ force due to gravity, or weight (N)
- $\mathrm{m}=$ mass $(\mathrm{kg})$
- This equations tells us:
- On planets with a large value of $g$, the gravitational force per unit mass is greater than on planets with a smaller value of $g$
- On such planets such as Jupiter, an object’s mass remains the same at all points in space. However, their weight will be a lot greater meaning for example, a human will be unable to fully stand up

A person’s weight on Jupiter would be so large a human would be unable to fully stand up
- The direction of a gravitational field is represented by gravitational field lines
- The gravitational field lines around a point mass are radially inwards
- The gravitational field lines of a uniform field, where the field strength is the same at all points, is represented by equally spaced parallel lines
- For example, the fields lines on the Earth’s surface
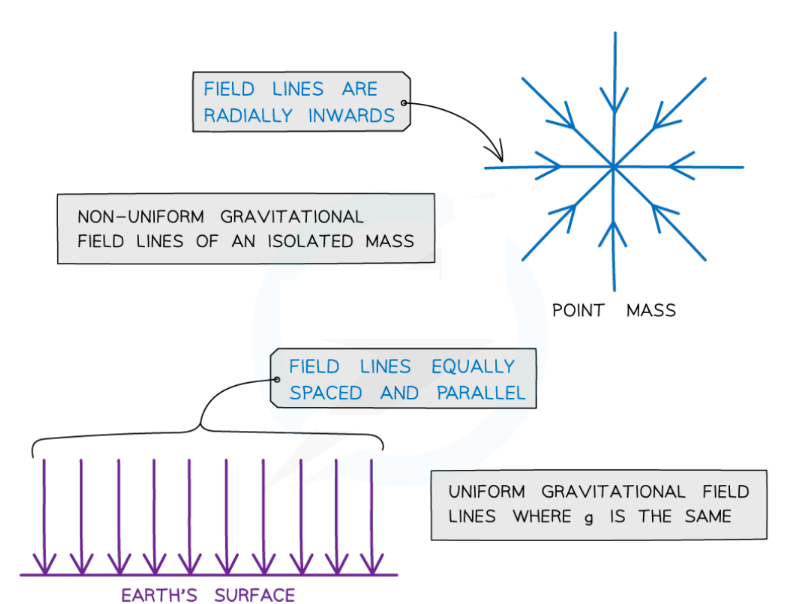
Gravitational field lines for a point mass and a uniform gravitational field
- Radial fields are considered non-uniform fields
- The gravitational field strength $g$ is different depending on how far you are from the centre
- Parallel field lines on the Earth’s surface are considered a uniform field
- The gravitational field strength $g$ is the same throughout
Exam Tip
Always label the arrows on the field lines! Gravitational forces are attractive only. Remember:
- For a radial field: it is towards the centre of the sphere or point charge
- For a uniform field: towards the surface of the object e.g. Earth
Worked example: Gravitational field
Calculate the mass of an object with weight $10 \mathrm{~N}$ on Earth.
Answer/Explanation
STEP 1 GRAVITATIONAL FIELD STRENGTH EQUATION
$
g=\frac{F_g}{m}
$
STEP 2 REARRANGE FOR MASS $\mathrm{m}$
$
m=\frac{F_g}{g}
$
STEP 3 SUBSTITUTE IN VALUES
$
\mathrm{m}=\frac{10}{9.81}=1.0 \mathrm{~kg}
$
Exam Tip
There is a big difference between $\mathrm{g}$ and $\mathrm{G}$ (sometimes referred to as ‘little $\mathrm{g}$ ‘ and ‘big G’ respectively), $g$ is the gravitational field strength and $\mathrm{G}$ is Newton’s gravitational constant. Make sure not to use these interchangeably!
Representing Gravitational Fields
Point Mass Approximation
- For a point outside a uniform sphere, the mass of the sphere may be considered to be a point mass at its centre
- A uniform sphere is one where its mass is distributed evenly
- The gravitational field lines around a uniform sphere are therefore identical to those around a point mass
- An object can be regarded as point mass when:
A body covers a very large distance as compared to its size, so, to study its motion, its size or dimensions can be neglected
- An example of this is field lines around planets
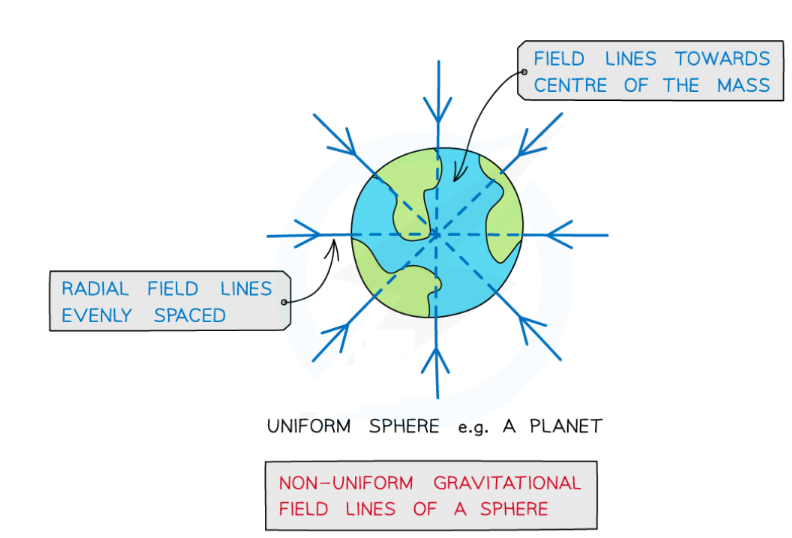
Gravitational field lines around a uniform sphere are identical to those on a point mass
- Radial fields are considered non-uniform fields
- So, the gravitational field strength $g$ is different depending on how far you are from the centre of mass of the sphere
