CIE AS/A Level Physics 13.2 Gravitational force between point masses Study Notes- 2025-2027 Syllabus
CIE AS/A Level Physics 13.2 Gravitational force between point masses Study Notes – New Syllabus
CIE AS/A Level Physics 13.2 Gravitational force between point masses Study Notes at IITian Academy focus on specific topic and type of questions asked in actual exam. Study Notes focus on AS/A Level Physics latest syllabus with Candidates should be able to:
- understand that, for a point outside a uniform sphere, the mass of the sphere may be considered to be a point mass at its centre
- recall and use Newton’s law of gravitation F = Gm1m2 / r2 for the force between two point masses
- analyse circular orbits in gravitational fields by relating the gravitational force to the centripetal acceleration it causes
- understand that a satellite in a geostationary orbit remains at the same point above the Earth’s surface, with an orbital period of 24 hours, orbiting from west to east, directly above the Equator
Gravitational Field of a Uniform Sphere — Point-Mass Approximation
For a point outside a uniform spherical mass, the gravitational effect of the entire sphere is the same as if all its mass were concentrated at its centre. This means the gravitational field and force due to a sphere behave as though it were a single point mass located at its centre.
Mathematical Statement:
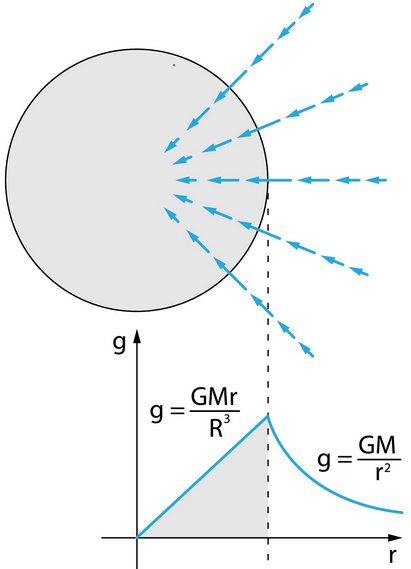
For any point outside a uniform sphere (radius \( \mathrm{R} \), mass \( \mathrm{M} \)), the gravitational field at a distance \( \mathrm{r} \geq R\) from the centre is given by \( \mathrm{g = \dfrac{GM}{r^2}.} \)
Explanation:
- This result comes from Newton’s shell theorem.
- Outside the sphere, the field behaves exactly like that of a point mass \( \mathrm{M} \) located at the centre.
- Inside the sphere (\( \mathrm{r < R} \)), the field varies linearly with \( \mathrm{r.} \)
Any spherical object (like Earth or a planet) can be treated as a point mass for gravitational calculations at points outside its surface.
Example
Calculate the gravitational field strength due to Earth at a point \( \mathrm{1.0 \times 10^7 \ m} \) from its centre. (Take \( \mathrm{M_E = 5.97 \times 10^{24} \ kg, \ G = 6.67 \times 10^{-11} \ N \, m^2 / kg^2.} \))
▶️ Answer / Explanation
Using \( \mathrm{g = \dfrac{GM}{r^2}} \):
\( \mathrm{g = \dfrac{6.67 \times 10^{-11} \times 5.97 \times 10^{24}}{(1.0 \times 10^7)^2}} \)
\( \mathrm{g = \dfrac{3.98 \times 10^{14}}{1.0 \times 10^{14}} = 3.98 \ N/kg.} \)
Hence, the field strength = \( \mathrm{3.98 \ N/kg.} \)
Interpretation: The Earth’s field at this distance acts as if all its mass were concentrated at its centre.
Example
The Moon has a radius of \( \mathrm{1.74 \times 10^6 \ m} \) and a mass of \( \mathrm{7.35 \times 10^{22} \ kg.} \) Determine the gravitational field strength halfway between the Earth and Moon. (Take \( \mathrm{M_E = 5.97 \times 10^{24} \ kg, \ R_{EM} = 3.84 \times 10^8 \ m, \ G = 6.67 \times 10^{-11}}. \))
▶️ Answer / Explanation
Let the point be at equal distance \( \mathrm{r = 1.92 \times 10^8 \ m} \) from both centres.
Earth’s field at point: \( \mathrm{g_E = \dfrac{GM_E}{r^2}} \)
\( \mathrm{g_E = \dfrac{6.67 \times 10^{-11} \times 5.97 \times 10^{24}}{(1.92 \times 10^8)^2} = 1.08 \times 10^{-2} \ N/kg.} \)
Moon’s field at point: \( \mathrm{g_M = \dfrac{GM_M}{r^2}} \)
\( \mathrm{g_M = \dfrac{6.67 \times 10^{-11} \times 7.35 \times 10^{22}}{(1.92 \times 10^8)^2} = 1.33 \times 10^{-4} \ N/kg.} \)
Net field strength (towards Earth):
\( \mathrm{g_{net} = g_E – g_M = 1.08 \times 10^{-2} – 1.33 \times 10^{-4} = 1.07 \times 10^{-2} \ N/kg.} \)
Hence, the resultant field halfway between Earth and Moon is approximately \( \mathrm{1.07 \times 10^{-2} \ N/kg,} \) directed towards Earth.
Key Insight: At points outside either body, each acts like a point mass, allowing the superposition of their gravitational fields.
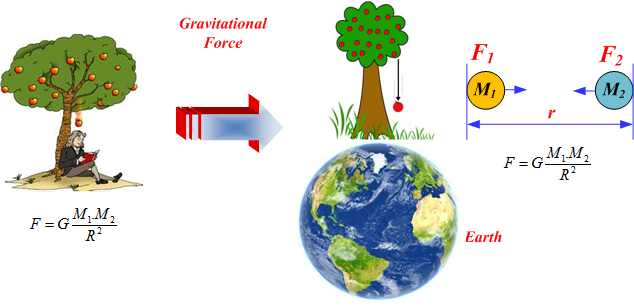
Newton’s Law of Gravitation
Statement: Every particle of matter in the universe attracts every other particle with a force that is:
- directly proportional to the product of their masses, and
- inversely proportional to the square of the distance between their centres.
Mathematical Form:
\( \mathrm{F = G \dfrac{m_1 m_2}{r^2}} \)
- \( \mathrm{F} \): gravitational force (N)
- \( \mathrm{m_1, m_2} \): interacting masses (kg)
- \( \mathrm{r} \): distance between their centres (m)
- \( \mathrm{G = 6.67 \times 10^{-11} \ N \, m^2 / kg^2} \): universal gravitational constant
Key Properties:
- The force acts along the line joining the centres of the two masses.
- It is mutual — both masses experience equal and opposite forces (Newton’s Third Law).
- It is always attractive in nature.
- It follows an inverse-square law: if the separation doubles, the force becomes one-fourth.
Example
Calculate the gravitational force between two \( \mathrm{5.0 \ kg} \) masses placed \( \mathrm{0.20 \ m} \) apart.
▶️ Answer / Explanation
Using \( \mathrm{F = G \dfrac{m_1 m_2}{r^2}} \):
\( \mathrm{F = 6.67 \times 10^{-11} \dfrac{5.0 \times 5.0}{(0.20)^2}} \)
\( \mathrm{F = 6.67 \times 10^{-11} \dfrac{25}{0.04} = 6.67 \times 10^{-11} \times 625 = 4.17 \times 10^{-8} \ N.} \)
Hence, \( \mathrm{F = 4.17 \times 10^{-8} \ N.} \)
Interpretation: This force is extremely small — illustrating why gravitational effects between small objects are negligible.
Example
Determine the gravitational force of attraction between Earth (\( \mathrm{M_E = 5.97 \times 10^{24} \ kg} \)) and the Moon (\( \mathrm{M_M = 7.35 \times 10^{22} \ kg} \)), given that the average Earth–Moon distance is \( \mathrm{3.84 \times 10^8 \ m.} \)
▶️ Answer / Explanation
Using \( \mathrm{F = G \dfrac{m_1 m_2}{r^2}} \):
\( \mathrm{F = 6.67 \times 10^{-11} \dfrac{(5.97 \times 10^{24})(7.35 \times 10^{22})}{(3.84 \times 10^8)^2}} \)
\( \mathrm{F = 6.67 \times 10^{-11} \dfrac{4.39 \times 10^{47}}{1.47 \times 10^{17}} = 6.67 \times 10^{-11} \times 2.99 \times 10^{30} = 1.99 \times 10^{20} \ N.} \)
Hence, the gravitational attraction between Earth and the Moon is \( \mathrm{1.99 \times 10^{20} \ N.} \)
Interpretation: This mutual force keeps the Moon in orbit around Earth — acting as the centripetal force for its circular motion.
Circular Orbits in Gravitational Fields
An object (such as a planet, moon, or satellite) in a stable circular orbit around a massive body moves under the influence of the gravitational force of that body. This gravitational force provides the centripetal force needed to keep the object moving in a circular path.
Equating Forces:
\( \mathrm{F_{gravity} = F_{centripetal}} \)
\( \mathrm{ \dfrac{GMm}{r^2} = \dfrac{mv^2}{r}} \)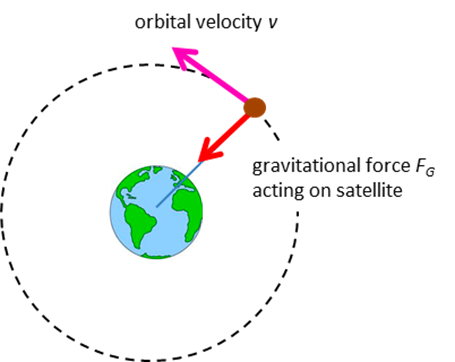
After simplification:
\( \mathrm{v^2 = \dfrac{GM}{r}} \quad \text{and} \quad \mathrm{v = \sqrt{\dfrac{GM}{r}}.} \)
- \( \mathrm{M} \): mass of the central body (e.g., Earth)
- \( \mathrm{m} \): mass of the orbiting body
- \( \mathrm{r} \): radius of orbit (distance from centre of central body)
- \( \mathrm{G} \): gravitational constant
- \( \mathrm{v} \): orbital speed
Orbital Period:
For one complete revolution, \( \mathrm{v = \dfrac{2\pi r}{T}} \). Substituting this into the earlier expression gives:
\( \mathrm{ \dfrac{4\pi^2r^2}{T^2} = \dfrac{GM}{r}} \Rightarrow \mathrm{T^2 = \dfrac{4\pi^2}{GM}r^3.} \)
This is Kepler’s Third Law: The square of the orbital period is proportional to the cube of the orbital radius for all circular orbits around the same central body.
In a circular orbit, the gravitational attraction of the central mass provides exactly the centripetal acceleration needed to maintain uniform circular motion.
Example
A satellite orbits Earth in a circular orbit of radius \( \mathrm{7.0 \times 10^6 \ m.} \) Given \( \mathrm{M_E = 5.97 \times 10^{24} \ kg} \) and \( \mathrm{G = 6.67 \times 10^{-11} \ N\,m^2/kg^2,} \) find the orbital speed and the period of the satellite.
▶️ Answer / Explanation
Step 1: Find orbital speed
\( \mathrm{v = \sqrt{\dfrac{GM}{r}} = \sqrt{\dfrac{6.67\times10^{-11} \times 5.97\times10^{24}}{7.0\times10^6}}.} \)
\( \mathrm{v = \sqrt{5.69\times10^7} = 7.55\times10^3 \ m/s.} \)
Step 2: Find period
\( \mathrm{T = \dfrac{2\pi r}{v} = \dfrac{2\pi \times 7.0\times10^6}{7.55\times10^3} = 5.83\times10^3 \ s = 1.62\ h.} \)
Hence: The satellite moves at \( \mathrm{7.55\ km/s} \) and completes one orbit every \( \mathrm{1.62\ hours.} \)
Interpretation: The gravitational force on the satellite is precisely equal to the centripetal force required for this circular motion.
Example
The Moon orbits Earth at a mean distance of \( \mathrm{3.84\times10^8 \ m.} \) Show that this distance is consistent with its orbital period of \( \mathrm{27.3\ days.} \)
▶️ Answer / Explanation
Step 1: Convert period to seconds
\( \mathrm{T = 27.3 \times 24 \times 3600 = 2.36\times10^6 \ s.} \)
Step 2: Using \( \mathrm{T^2 = \dfrac{4\pi^2}{GM}r^3} \Rightarrow r^3 = \dfrac{GMT^2}{4\pi^2}} \)
\( \mathrm{r^3 = \dfrac{6.67\times10^{-11} \times 5.97\times10^{24} \times (2.36\times10^6)^2}{4\pi^2}} \)
\( \mathrm{r^3 = 5.64\times10^{25} \Rightarrow r = (5.64\times10^{25})^{1/3} = 3.82\times10^8 \ m.} \)
Result: The computed radius \( \mathrm{3.82\times10^8 \ m} \) matches the actual orbital distance, confirming the validity of Newton’s law and centripetal relationship.
Interpretation: The Moon’s orbit is stable because the gravitational pull of Earth provides the exact centripetal acceleration required for its circular motion.
Geostationary Orbits
A geostationary satellite (also called a geosynchronous equatorial satellite) is one that:
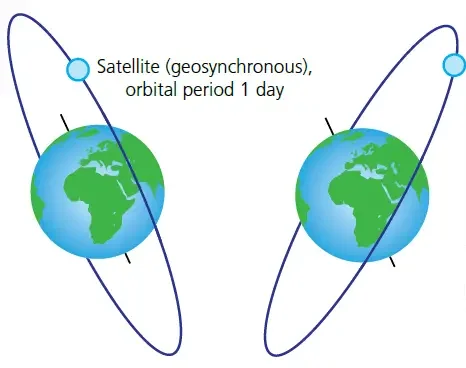
- Remains at a fixed position above a point on Earth’s surface,
- Has an orbital period of 24 hours, matching Earth’s rotation,
- Orbits from west to east, in the same direction as Earth’s rotation,
- Orbits directly above the Equator (0° latitude).
Condition for Geostationary Orbit:
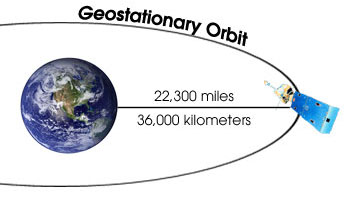
\( \mathrm{T = 24\ hours = 86400\ s.} \)
Substitute into the relation \( \mathrm{T^2 = \dfrac{4\pi^2r^3}{GM_E}} \) to find the orbital radius \( \mathrm{r.} \)
\( \mathrm{r^3 = \dfrac{GMT^2}{4\pi^2} \Rightarrow r = \left(\dfrac{6.67\times10^{-11}\times5.97\times10^{24}\times(86400)^2}{4\pi^2}\right)^{1/3} = 4.22\times10^7\ m.} \)
Hence: Orbital radius from Earth’s centre = \( \mathrm{4.22\times10^7\ m.} \) Altitude above surface = \( \mathrm{4.22\times10^7 – 6.37\times10^6 = 3.58\times10^7\ m \approx 36,000\ km.} \)
Applications:
- Communications and weather satellites (e.g., INSAT, GOES, Intelsat).
- Used for constant coverage of the same Earth region.
A geostationary satellite stays fixed relative to a point on Earth because its orbital angular velocity equals Earth’s rotational angular velocity.
Example
Show that a geostationary satellite with a period of 24 hours must orbit at a height of approximately \( \mathrm{36,000 \ km.} \)
▶️ Answer / Explanation
Given: \( \mathrm{T = 86400\ s, \ M_E = 5.97\times10^{24}\ kg, \ G = 6.67\times10^{-11}.} \)
Using \( \mathrm{r^3 = \dfrac{GMT^2}{4\pi^2}} \):
\( \mathrm{r = \left(\dfrac{6.67\times10^{-11}\times5.97\times10^{24}\times(86400)^2}{4\pi^2}\right)^{1/3} = 4.22\times10^7\ m.} \)
Altitude above Earth = \( \mathrm{r – R_E = 4.22\times10^7 – 6.37\times10^6 = 3.58\times10^7\ m.} \)
Hence: The satellite’s altitude is about \( \mathrm{36,000\ km.} \)
Example
A satellite of mass \( \mathrm{1500\ kg} \) is placed in a circular geostationary orbit around Earth. Determine (a) its orbital speed, and (b) the gravitational force acting on it.
▶️ Answer / Explanation
Given: \( \mathrm{r = 4.22\times10^7\ m, \ M_E = 5.97\times10^{24}\ kg, \ G = 6.67\times10^{-11}.} \)
(a) Orbital speed:
\( \mathrm{v = \sqrt{\dfrac{GM}{r}} = \sqrt{\dfrac{6.67\times10^{-11}\times5.97\times10^{24}}{4.22\times10^7}} = 3.07\times10^3\ m/s.} \)
(b) Gravitational force:
\( \mathrm{F = \dfrac{GMm}{r^2} = \dfrac{6.67\times10^{-11}\times5.97\times10^{24}\times1500}{(4.22\times10^7)^2} = 3.36\times10^4\ N.} \)
Hence:
- Orbital speed = \( \mathrm{3.07\ km/s.} \)
- Gravitational force = \( \mathrm{3.36\times10^4\ N.} \)
Interpretation: At this altitude and speed, the satellite remains fixed above the same location on Earth — ideal for communication and weather monitoring systems.
