CIE AS/A Level Physics 13.3 Gravitational field of a point mass Study Notes- 2025-2027 Syllabus
CIE AS/A Level Physics 13.3 Gravitational field of a point mass Study Notes – New Syllabus
CIE AS/A Level Physics 13.3 Gravitational field of a point mass Study Notes at IITian Academy focus on specific topic and type of questions asked in actual exam. Study Notes focus on AS/A Level Physics latest syllabus with Candidates should be able to:
- derive, from Newton’s law of gravitation and the definition of gravitational field, the equation g = GM / r 2 for the gravitational field strength due to a point mass
- recall and use g = GM / r 2
- understand why g is approximately constant for small changes in height near the Earth’s surface
Deriving \( \mathrm{g = \dfrac{GM}{r^2}} \) from Newton’s Law of Gravitation
The gravitational field strength at a point is defined as the force per unit mass experienced by a small test mass placed at that point.

Definition of Gravitational Field Strength:
\( \mathrm{g = \dfrac{F}{m}} \)
According to Newton’s Law of Gravitation, the gravitational force \( \mathrm{F} \) between two point masses \( \mathrm{M} \) and \( \mathrm{m} \) separated by a distance \( \mathrm{r} \) is:
\( \mathrm{F = G\dfrac{Mm}{r^2}} \)
Substituting this expression for \( \mathrm{F} \) into the definition of \( \mathrm{g} \):
\( \mathrm{g = \dfrac{F}{m} = \dfrac{G\dfrac{Mm}{r^2}}{m} = \dfrac{GM}{r^2}.} \)
Hence,
\( \mathrm{g = \dfrac{GM}{r^2}} \)
- \( \mathrm{g} \): gravitational field strength (N/kg or m/s²)
- \( \mathrm{G} \): universal gravitational constant (\( \mathrm{6.67\times10^{-11}\ N\,m^2/kg^2} \))
- \( \mathrm{M} \): mass of the source (kg)
- \( \mathrm{r} \): distance from the centre of mass (m)
Key Features of \( \mathrm{g = \dfrac{GM}{r^2}} \):
- Field strength decreases with the square of the distance (inverse-square law).
- \( \mathrm{g} \) is directly proportional to the mass of the attracting body.
- The direction of \( \mathrm{g} \) is always towards the centre of the mass producing the field (attractive).
Example
Determine the gravitational field strength at a point \( \mathrm{2.0\times10^7\ m} \) from the centre of Earth. Take \( \mathrm{G = 6.67\times10^{-11}\ N\,m^2/kg^2, \ M_E = 5.97\times10^{24}\ kg.} \)
▶️ Answer / Explanation
Using \( \mathrm{g = \dfrac{GM}{r^2}} \):
\( \mathrm{g = \dfrac{6.67\times10^{-11} \times 5.97\times10^{24}}{(2.0\times10^7)^2}} \)
\( \mathrm{g = \dfrac{3.98\times10^{14}}{4.0\times10^{14}} = 0.995\ N/kg.} \)
Hence: \( \mathrm{g = 0.995\ N/kg.} \)
Interpretation: The gravitational field strength decreases rapidly with increasing distance from Earth’s centre due to the inverse-square relationship.
Example
At what distance from the centre of Earth will the gravitational field strength be \( \mathrm{1.5\ N/kg?} \) Take \( \mathrm{G = 6.67\times10^{-11}\ N\,m^2/kg^2, \ M_E = 5.97\times10^{24}\ kg.} \)
▶️ Answer / Explanation
From \( \mathrm{g = \dfrac{GM}{r^2}} \), rearrange for \( \mathrm{r:} \)
\( \mathrm{r = \sqrt{\dfrac{GM}{g}}.} \)
Substitute values:
\( \mathrm{r = \sqrt{\dfrac{6.67\times10^{-11}\times5.97\times10^{24}}{1.5}} = \sqrt{2.65\times10^{14}} = 1.63\times10^7\ m.} \)
Hence: The field strength becomes \( \mathrm{1.5\ N/kg} \) at a distance of \( \mathrm{1.63\times10^7\ m} \) from Earth’s centre.
Interpretation: This corresponds to an altitude of \( \mathrm{1.63\times10^7 – 6.37\times10^6 = 9.9\times10^6\ m} \), i.e., about 9900 km above Earth’s surface — a region near medium Earth orbit (MEO).
Recall and Use of \( \mathrm{g = \dfrac{GM}{r^2}} \)
Formula: The gravitational field strength at a distance \( \mathrm{r} \) from a point mass \( \mathrm{M} \) is:![]()
\( \mathrm{g = \dfrac{GM}{r^2}} \)
Key Relationships:
- \( \mathrm{g \propto \dfrac{1}{r^2}} \): the field strength decreases rapidly with distance.
- \( \mathrm{g \propto M} \): doubling the mass doubles the field strength at a given point.
- Direction: towards the mass producing the field (attractive).
Graphical Representation:
The inverse-square relationship means that if the distance from a mass is doubled, the gravitational field strength becomes one-quarter of its original value.
Example
The gravitational field strength at Earth’s surface is \( \mathrm{9.81\ N/kg.} \) Calculate the field strength at a height equal to Earth’s radius above the surface. (\( \mathrm{R_E = 6.37\times10^6\ m.} \))
▶️ Answer / Explanation
Total distance from Earth’s centre: \( \mathrm{r = 2R_E = 2 \times 6.37\times10^6 = 1.27\times10^7\ m.} \)
Since \( \mathrm{g \propto \dfrac{1}{r^2}} \):
\( \mathrm{g’ = g \left(\dfrac{R_E}{r}\right)^2 = 9.81 \left(\dfrac{6.37\times10^6}{1.27\times10^7}\right)^2 = 9.81 \times \left(\dfrac{1}{2}\right)^2 = 9.81 \times 0.25 = 2.45\ N/kg.} \)
Hence: \( \mathrm{g’ = 2.45\ N/kg.} \)
Interpretation: At twice the distance from the centre, gravitational field strength falls to one-quarter of its surface value.
Example
Two planets, A and B, have the same radius. Planet A has twice the mass of Planet B. If the gravitational field strength at the surface of B is \( \mathrm{5.0\ N/kg,} \) determine the field strength at the surface of A.
▶️ Answer / Explanation
Using \( \mathrm{g = \dfrac{GM}{r^2}} \):
Since both planets have the same radius, \( \mathrm{r} \) is constant. Hence, \( \mathrm{g \propto M.} \)
Given \( \mathrm{M_A = 2M_B} \):
\( \mathrm{g_A = 2g_B = 2 \times 5.0 = 10.0\ N/kg.} \)
Hence: The gravitational field strength at the surface of Planet A is \( \mathrm{10.0\ N/kg.} \)
Interpretation: Doubling the planet’s mass doubles the surface gravitational field strength (assuming constant radius).
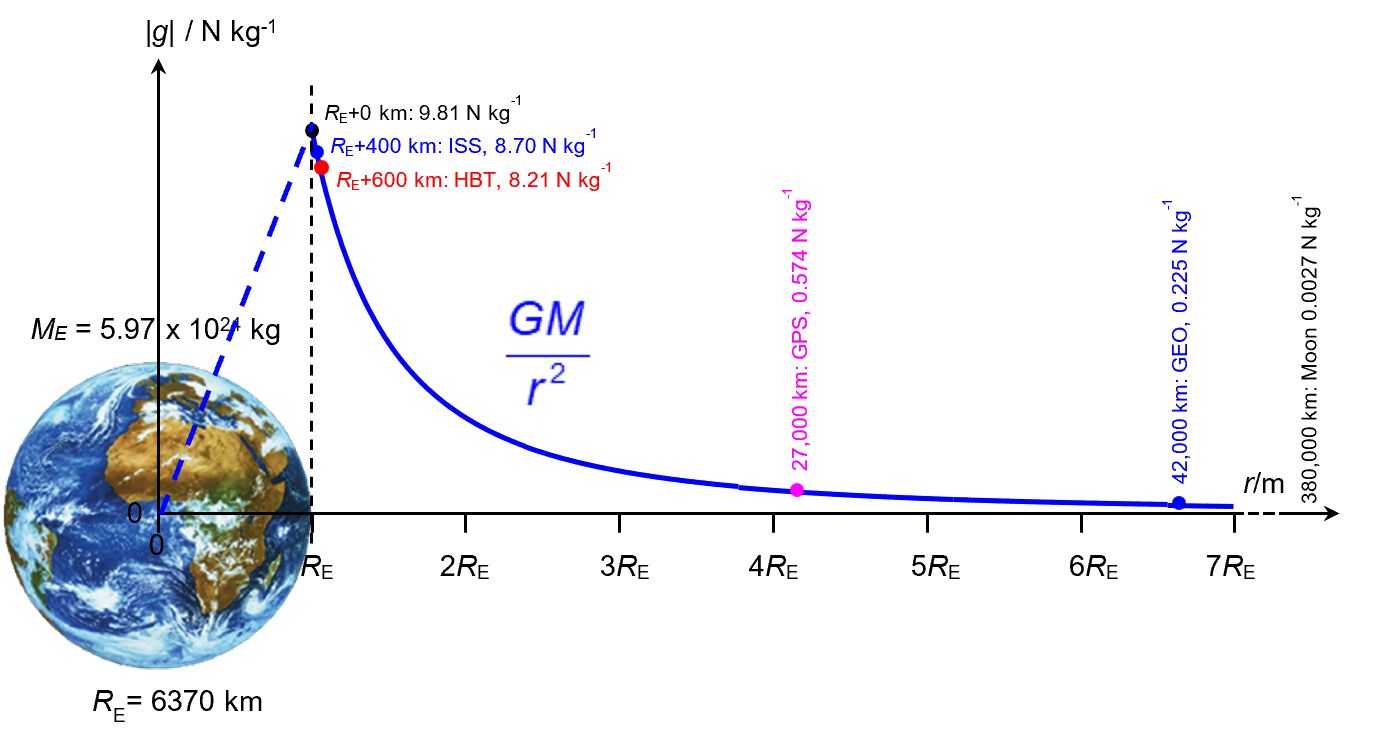
Variation of Gravitational Field Strength Near the Earth’s Surface
The gravitational field strength \( \mathrm{g} \) at a distance \( \mathrm{r} \) from the centre of Earth is given by:
\( \mathrm{g = \dfrac{GM_E}{r^2}} \)
For points close to Earth’s surface, \( \mathrm{r = R_E + h}\), where:
- \( \mathrm{R_E} \): Earth’s radius (\( \mathrm{6.37\times10^6\ m} \))
- \( \mathrm{h} \): height above Earth’s surface
- \( \mathrm{h \ll R_E} \) (very small compared to Earth’s radius)
We can therefore analyze why ( \mathrm{g} ) changes very little for small ( \mathrm{h.} )
Mathematical Reasoning:
At a height \( \mathrm{h} \) above Earth’s surface:
\( \mathrm{g_h = \dfrac{GM_E}{(R_E + h)^2}} \)
The ratio of field strengths at height ( \mathrm{h} ) and at the surface is:
\( \mathrm{\dfrac{g_h}{g_0} = \dfrac{R_E^2}{(R_E + h)^2}} \)
When \( \mathrm{h \ll R_E,} \) we can expand using the binomial approximation:
\( \mathrm{(R_E + h)^{-2} \approx R_E^{-2}(1 – \dfrac{2h}{R_E})} \)
Substituting gives:
\( \mathrm{g_h \approx g_0 \left(1 – \dfrac{2h}{R_E}\right)} \)
Interpretation:
- The fractional change in \( \mathrm{g} \) is \( \mathrm{\dfrac{\Delta g}{g} \approx -\dfrac{2h}{R_E}}. \)
- Since \( \mathrm{R_E = 6.37\times10^6\ m,} \) even for \( \mathrm{h = 1000\ m,} \) \( \mathrm{\dfrac{2h}{R_E} = 3.14\times10^{-4} = 0.03\%.} \)
- This means \( \mathrm{g} \) decreases by only about 0.03% per kilometre of altitude negligible for everyday scales.
Hence:
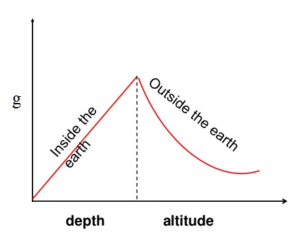
For small heights near Earth’s surface, \( \mathrm{R_E + h \approx R_E,} \) so the change in \( \mathrm{g} \) is extremely small, and \( \mathrm{g} \) can be treated as approximately constant.
Example
Show that the gravitational field strength decreases by less than 0.05% when moving from the surface to 1 km above Earth’s surface.
▶️ Answer / Explanation
Fractional change: \( \mathrm{\dfrac{\Delta g}{g} = -\dfrac{2h}{R_E}} \)
\( \mathrm{= -\dfrac{2\times1000}{6.37\times10^6} = -3.14\times10^{-4}.} \)
Percentage change = \( \mathrm{0.0314\%.} \)
Hence: The decrease in \( \mathrm{g} \) is only about 0.03%, negligible in practice — so \( \mathrm{g} \approx 9.81\ N/kg.} \)
Example
An aircraft flies at a height of \( \mathrm{10\ km.} \) Calculate the gravitational field strength at that altitude and compare it to its value at the surface (\( \mathrm{g_0 = 9.81\ N/kg.} \)).
▶️ Answer / Explanation
At altitude \( \mathrm{h = 1.0\times10^4\ m,} \) total distance from Earth’s centre: \( \mathrm{r = R_E + h = 6.37\times10^6 + 1.0\times10^4 = 6.38\times10^6\ m.} \)
Using the ratio \( \mathrm{g_h = g_0 \left(\dfrac{R_E}{R_E + h}\right)^2:} \)
\( \mathrm{g_h = 9.81 \left(\dfrac{6.37\times10^6}{6.38\times10^6}\right)^2 = 9.81 (0.9984)^2 = 9.78\ N/kg.} \)
Hence: At 10 km altitude, \( \mathrm{g = 9.78\ N/kg,} \) only 0.3% less than at the surface.
Interpretation: Even at typical aircraft altitudes, \( \mathrm{g} \) remains almost constant — allowing us to treat near-surface gravitational acceleration as uniform.
