CIE AS/A Level Physics 15.1 The mole Study Notes- 2025-2027 Syllabus
CIE AS/A Level Physics 15.1 The mole Study Notes – New Syllabus
CIE AS/A Level Physics 15.1 The mole Study Notes at IITian Academy focus on specific topic and type of questions asked in actual exam. Study Notes focus on AS/A Level Physics latest syllabus with Candidates should be able to:
- understand that amount of substance is an SI base quantity with the base unit mol
- use molar quantities where one mole of any substance is the amount containing a number of particles of that substance equal to the Avogadro constant NA
Amount of Substance
The amount of substance is an SI base quantity that measures how many particles (atoms, molecules, ions, electrons, etc.) are present in a sample. Its SI base unit is the mole (mol).
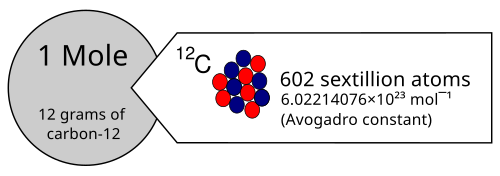
Key Explanation:
- One mole contains exactly \( \mathrm{6.022 \times 10^{23}} \) particles (Avogadro’s constant).
- It is a fundamental quantity in chemistry and physics used to count microscopic particles in macroscopic amounts of matter.
- The amount of substance is independent of the type of particle; it only depends on the number of particles.
SI Base Status: The mole is one of the seven SI base units (alongside metre, kilogram, second, ampere, kelvin, candela).
Amount of substance tells us “how many particles” are present, and the mole is the standard unit used to count them.
Summary
| Concept | Description |
|---|---|
| Amount of substance | SI base quantity for counting particles |
| Unit: mole (mol) | 1 mol = \( \mathrm{6.022 \times 10^{23}} \) particles |
| Purpose | Allows counting of microscopic particles via macroscopic measurements |
The mole is an SI base unit used to measure the amount of substance essentially a counting unit for particles.
Example
How many moles are present in a sample containing \( \mathrm{6.022 \times 10^{23}} \) molecules of water?
▶️ Answer / Explanation
This is exactly one mole by definition.
So the sample contains 1 mol of water molecules.
Example
A container holds \( \mathrm{1.204 \times 10^{24}} \) atoms of helium. How many moles of helium is this?
▶️ Answer / Explanation
Use:
Number of moles \( \mathrm{= \dfrac{N}{N_A}} \)
\( \mathrm{= \dfrac{1.204\times 10^{24}}{6.022\times 10^{23}} = 2.00 \ mol} \)
The container holds 2 moles of helium.
Example
A sample contains \( \mathrm{3.01 \times 10^{23}} \) molecules of \( \mathrm{CO_2} \). How many moles is this, and how many atoms does this correspond to?
▶️ Answer / Explanation
Step 1: Calculate the moles of CO₂
\( \mathrm{n = \dfrac{3.01\times 10^{23}}{6.022\times 10^{23}} = 0.50 \ mol} \)
Step 2: Count the number of atoms
- Each CO₂ molecule contains 3 atoms (1 carbon + 2 oxygen).
Total atoms \( \mathrm{= 3 \times 3.01\times 10^{23}} = 9.03\times 10^{23}} \)
Final Answer:
0.50 mol of CO₂ corresponds to \( \mathrm{9.03 \times 10^{23}} \) total atoms.
Molar Quantities and the Avogadro Constant
One mole of any substance is defined as the amount that contains exactly \( \mathrm{N_A = 6.022 \times 10^{23}} \) particles. This value is called the Avogadro constant.

Key Relationship:
\( \mathrm{n = \dfrac{N}{N_A}} \)
\( \mathrm{N = nN_A} \)
Where:
- \( \mathrm{n} \) = amount of substance in moles
- \( \mathrm{N} \) = number of particles (atoms, molecules, ions)
- \( \mathrm{N_A = 6.022\times 10^{23} \ mol^{-1}} \)
A mole allows us to count extremely large numbers of particles using a measurable quantity.
Summary Table
| Quantity | Description |
|---|---|
| Avogadro Constant | \( \mathrm{N_A = 6.022\times 10^{23} \ particles \ per \ mole} \) |
| Mole (mol) | The amount of substance containing \( \mathrm{N_A} \) particles |
| To find moles | \( \mathrm{n = \dfrac{N}{N_A}} \) |
| To find number of particles | \( \mathrm{N = nN_A} \) |
Example
How many particles are in 3 moles of a substance?
▶️ Answer / Explanation
\( \mathrm{N = nN_A = 3 \times 6.022\times 10^{23}} \)
= \( \mathrm{1.806\times 10^{24}} \) particles
Example
A sample contains \( \mathrm{1.505\times 10^{24}} \) atoms of sodium. How many moles of sodium are present?
▶️ Answer / Explanation
\( \mathrm{n = \dfrac{1.505\times 10^{24}}{6.022\times 10^{23}} = 2.50 \ mol} \)
The sample contains 2.50 mol of sodium.
Example
A substance has the formula \( \mathrm{AB_2} \). You have \( \mathrm{9.033\times 10^{23}} \) atoms of B. Find:
- (a) the number of formula units of \( \mathrm{AB_2} \)
- (b) the moles of \( \mathrm{AB_2} \)
- (c) the moles of A atoms
▶️ Answer / Explanation
(a) Formula units
Each formula unit contains 2 atoms of B, so:
\( \mathrm{Formula\ units = \dfrac{9.033\times 10^{23}}{2} = 4.5165\times 10^{23}} \)
(b) Moles of AB₂
\( \mathrm{n = \dfrac{4.5165\times 10^{23}}{6.022\times 10^{23}} = 0.75 \ mol} \)
(c) Moles of A atoms
Each formula unit has 1 atom of A, so:
Number of A atoms = number of formula units
Moles of A = \( \mathrm{0.75 \ mol} \)
Final Answers:
- (a) \( \mathrm{4.5165\times 10^{23}} \) formula units
- (b) \( \mathrm{0.75 \ mol} \)
- (c) \( \mathrm{0.75 \ mol} \) of A atoms
