CIE AS/A Level Physics 17.1 Simple harmonic oscillations Study Notes- 2025-2027 Syllabus
CIE AS/A Level Physics 17.1 Simple harmonic oscillations Study Notes – New Syllabus
CIE AS/A Level Physics 17.1 Simple harmonic oscillations Study Notes at IITian Academy focus on specific topic and type of questions asked in actual exam. Study Notes focus on AS/A Level Physics latest syllabus with Candidates should be able to:
- understand and use the terms displacement, amplitude, period, frequency, angular frequency and phase difference in the context of oscillations, and express the period in terms of both frequency and angular frequency
- understand that simple harmonic motion occurs when acceleration is proportional to displacement from a fixed point and in the opposite direction
- use $a = -{\omega}^{2}x$ and recall and use, as a solution to this equation, $x = x_0 \sin \omega t$
- use the equations $v = v_0 \cos \omega t$ and $v = \pm \omega \sqrt{\left(x_0^{2} – x^{2}\right)}$
- analyse and interpret graphical representations of the variations of displacement, velocity and acceleration for simple harmonic motion
Key Terms in Oscillations
Oscillatory motion involves repeated movement about an equilibrium position. The following terms describe various aspects of this motion.
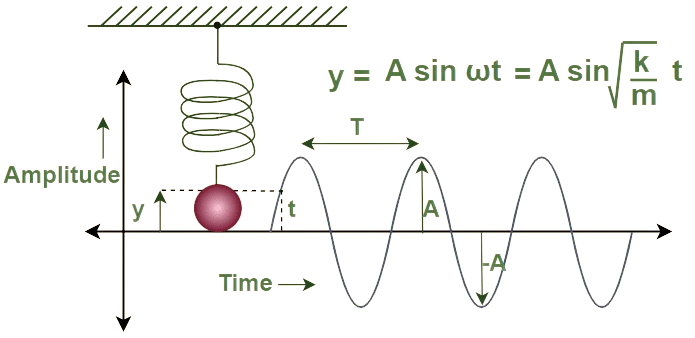
Displacement
The distance and direction of an oscillating particle from its equilibrium position at any instant.
Amplitude (A)
The maximum displacement of the particle from the equilibrium position.
Period (T)
The time taken for one complete cycle of oscillation.
Frequency (f)
The number of complete oscillations per second. Measured in hertz (Hz).
\( \mathrm{f = \frac{1}{T}} \)
Angular Frequency (ω)
A measure of how rapidly the oscillation cycles in radians per second.
\( \mathrm{\omega = 2\pi f = \frac{2\pi}{T}} \)
Phase Difference (ϕ)
The difference in the positions within the cycle of two oscillating particles, expressed in radians or degrees.
A full cycle corresponds to \( \mathrm{2\pi} \) radians or 360°.
Example
A pendulum completes one oscillation every 2 seconds. Find its frequency.
▶️ Answer / Explanation
Given period \( \mathrm{T = 2\ s} \)
\( \mathrm{f = \frac{1}{T} = \frac{1}{2} = 0.5\ Hz} \)
The frequency is 0.5 Hz.
Example
An oscillation has a frequency of \( \mathrm{5\ Hz} \). Calculate the angular frequency.
▶️ Answer / Explanation
Use \( \mathrm{\omega = 2\pi f} \):
\( \mathrm{\omega = 2\pi \times 5 = 10\pi\ rad\,s^{-1}} \)
Angular frequency = \( \mathrm{10\pi\ rad\,s^{-1}} \).
Example
Two oscillators A and B have the same amplitude and frequency. Oscillator A reaches maximum displacement at \( \mathrm{t = 0\ s} \), while B reaches maximum displacement at \( \mathrm{t = 0.25\ s} \). If the period of oscillation is \( \mathrm{T = 1.0\ s} \), find the phase difference between A and B.
▶️ Answer / Explanation
Time difference between their maxima:
\( \mathrm{\Delta t = 0.25\ s} \)
Phase difference formula:
\( \mathrm{\phi = 2\pi \frac{\Delta t}{T}} \)
Substitute:
\( \mathrm{\phi = 2\pi \frac{0.25}{1.0} = \frac{2\pi}{4} = \frac{\pi}{2}} \)
The phase difference is \( \mathrm{\frac{\pi}{2}\ rad} \) (or 90°).
Condition for Simple Harmonic Motion (SHM)
Simple harmonic motion occurs when the acceleration of an object is:
- directly proportional to its displacement from a fixed equilibrium point, and
- always directed towards that equilibrium point (opposite direction to displacement).
This condition can be expressed mathematically as:
\( \mathrm{a \propto -x} \)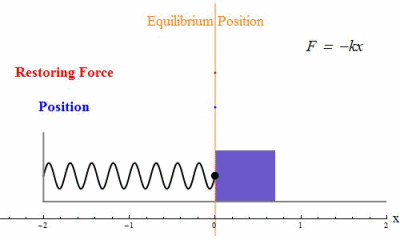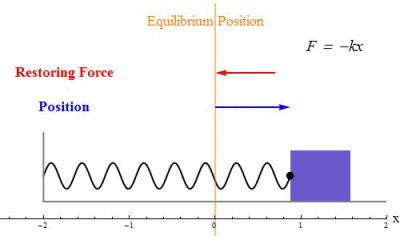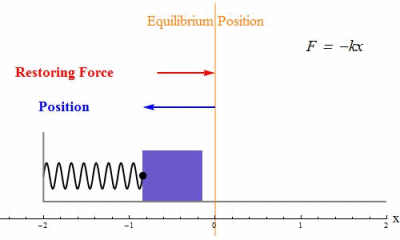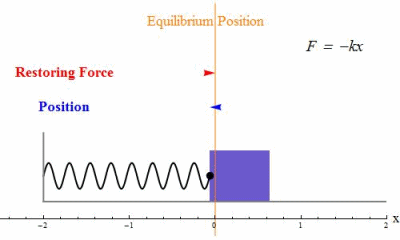
or more precisely:
\( \mathrm{a = -\omega^2 x} \)
- \( \mathrm{a} \) = acceleration
- \( \mathrm{x} \) = displacement
- \( \mathrm{\omega} \) = angular frequency
Key Meaning:
The further the object is displaced from equilibrium, the greater the restoring acceleration pulling it back. This restoring action produces oscillatory motion.
Essential Characteristics:
- Acceleration is maximum at maximum displacement.
- Acceleration is zero at the equilibrium position.
- Motion is sinusoidal (described by sine or cosine functions).
Example
A mass on a spring is pulled 5 cm from its equilibrium position and released. Explain why this motion is simple harmonic.
▶️ Answer / Explanation
The spring provides a restoring force proportional to displacement: \( \mathrm{F = -kx} \). Since \( \mathrm{a = F/m} \), acceleration is also proportional to displacement and directed towards equilibrium. Thus, the motion is simple harmonic.
Example
An object oscillates with acceleration given by \( \mathrm{a = -25x} \). Show that the motion is SHM and determine the angular frequency.
▶️ Answer / Explanation
The acceleration has the form:
\( \mathrm{a = -\omega^2 x} \)
Compare:
\( \mathrm{-\omega^2 = -25} \Rightarrow \omega^2 = 25 \)
Thus:
\( \mathrm{\omega = 5\ rad\,s^{-1}} \)
The motion is SHM because acceleration is proportional to displacement and negative (restoring).
Example
A particle moves such that its acceleration is given by \( \mathrm{a = -4\pi^2 x} \). At maximum displacement \( \mathrm{x = 0.10\ m} \), find the maximum acceleration and explain the SHM condition.
▶️ Answer / Explanation
The formula matches SHM:
\( \mathrm{a = -\omega^2 x} \)
So:
\( \mathrm{\omega^2 = 4\pi^2} \Rightarrow \omega = 2\pi\ rad\,s^{-1}} \)
Maximum acceleration occurs at maximum displacement:
\( \mathrm{a_{max} = -\omega^2 x_{max}} \)
\( \mathrm{a_{max} = -(4\pi^2)(0.10) = -1.26\ m\,s^{-2}} \)
The negative sign shows the acceleration is towards equilibrium — confirming SHM.
Acceleration–Displacement Relationship and SHM Solution
For simple harmonic motion (SHM), the acceleration is always:
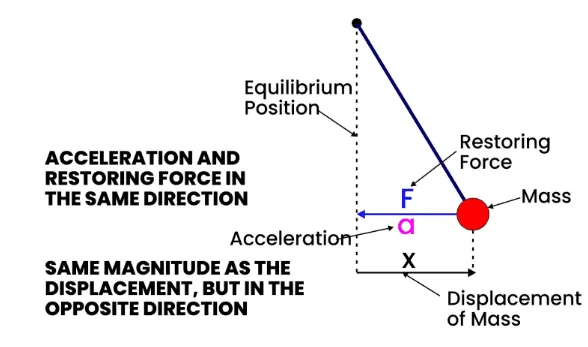
\( \mathrm{a = -\omega^2 x} \)
- The acceleration is proportional to displacement.
- The negative sign shows it is directed towards the equilibrium position.
- \( \mathrm{\omega} \) is the angular frequency (rad s⁻¹).
Solution to the SHM Equation:
The differential equation \( \mathrm{a = -\omega^2 x} \) has a general solution for displacement: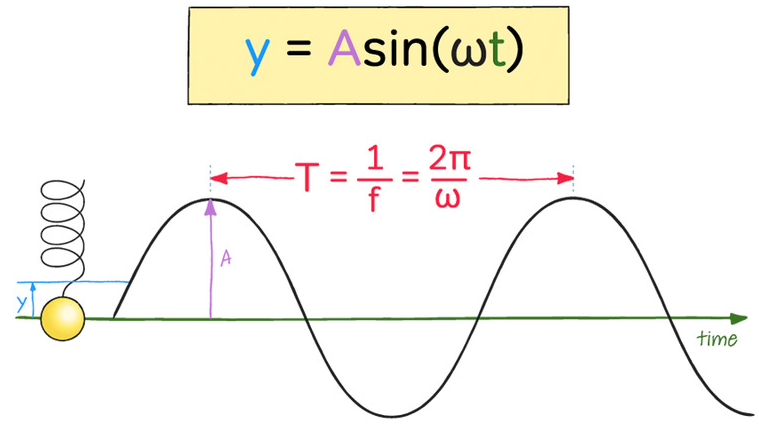
\( \mathrm{x = x_0 \sin(\omega t)} \)
- \( \mathrm{x} \) = displacement at time \( \mathrm{t} \)
- \( \mathrm{x_0} \) = amplitude (maximum displacement)
- \( \mathrm{\omega} \) = angular frequency
- \( \mathrm{t} \) = time
Interpretation:
The motion is sinusoidal the particle moves back and forth following a smooth sine curve, characteristic of SHM.
Example
A particle moves according to \( \mathrm{x = 0.08\sin(10t)} \). What are the amplitude and angular frequency of the oscillation?
▶️ Answer / Explanation
- Compare with \( \mathrm{x = x_0 \sin(\omega t)} \).
- Amplitude \( \mathrm{x_0 = 0.08\ m} \)
- Angular frequency \( \mathrm{\omega = 10\ rad\,s^{-1}} \)
The amplitude is 0.08 m and the angular frequency is 10 rad s⁻¹.
Example
An oscillator obeys \( \mathrm{a = -36x} \). Find the displacement function \( \mathrm{x(t)} \) in the form \( \mathrm{x = x_0 \sin(\omega t)} \).
▶️ Answer / Explanation
Match with the SHM form:
\( \mathrm{a = -\omega^2 x} \)
So:
\( \mathrm{\omega^2 = 36 \Rightarrow \omega = 6\ rad\,s^{-1}} \)
Thus, the solution is:
\( \mathrm{x = x_0 \sin(6t)} \)
The amplitude \( x_0 \) depends on initial conditions and can be any constant.
Example
A particle performs SHM with equation \( \mathrm{x = 0.12\sin(4\pi t)} \). Find its acceleration when the displacement is \( \mathrm{x = 0.06\ m} \).
▶️ Answer / Explanation
Angular frequency is:
\( \mathrm{\omega = 4\pi} \)
Use SHM formula:
\( \mathrm{a = -\omega^2 x} \)
Substitute:
\( \mathrm{a = -(4\pi)^2 (0.06)} \)
\( \mathrm{a = -(16\pi^2)(0.06)} \)
\( \mathrm{a = -0.96\pi^2\ m\,s^{-2}} \)
Numerically:
\( \mathrm{a \approx -9.5\ m\,s^{-2}} \)
The acceleration is approximately \( \mathrm{-9.5\ m\,s^{-2}} \), directed toward equilibrium.
Velocity in Simple Harmonic Motion (SHM)
For a particle undergoing SHM with displacement: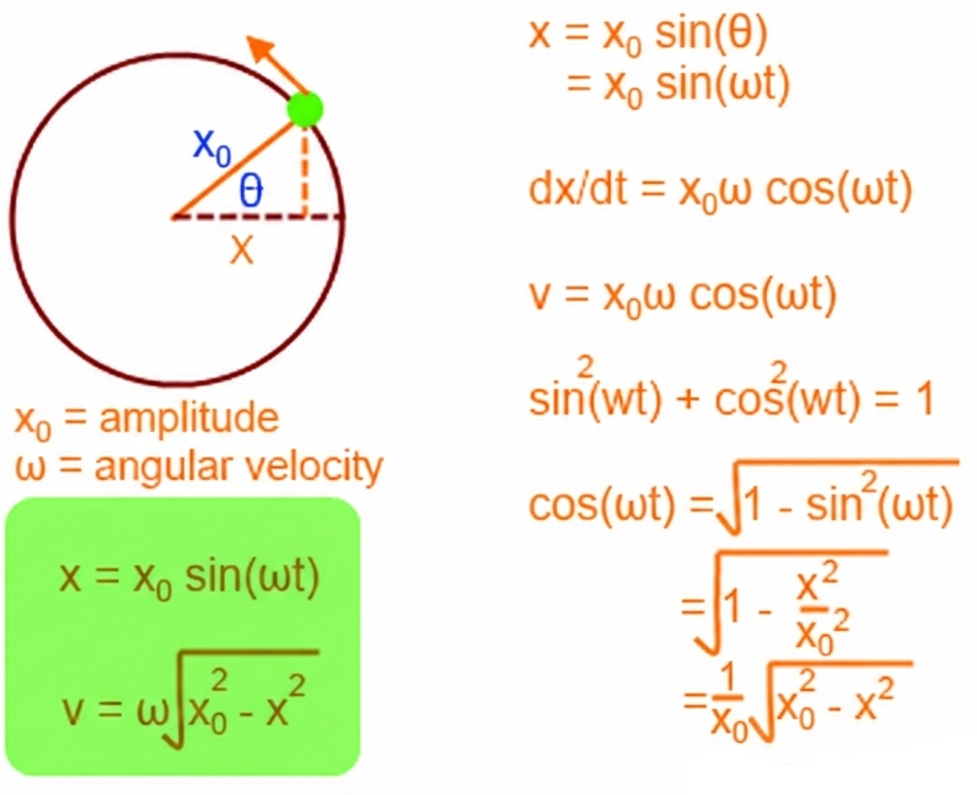
\( \mathrm{x = x_0 \sin(\omega t)} \)
the velocity of the particle can be expressed in two important forms:
1. Velocity as a function of time
\( \mathrm{v = v_0 \cos(\omega t)} \)
- \( \mathrm{v_0 = \omega x_0} \) is the maximum velocity
- \( \mathrm{v} \) is the instantaneous velocity
- The velocity is 90° (or \( \pi/2 \)) ahead of displacement in phase
Meaning: Velocity is maximum at equilibrium and zero at maximum displacement.
2. Velocity as a function of displacement
\( \mathrm{v = \pm \omega \sqrt{x_0^2 – x^2}} \)
- The \( \pm \) sign indicates direction of motion
- Velocity decreases as the particle moves away from equilibrium
- Velocity becomes zero at \( \mathrm{x = \pm x_0} \)
Meaning: The speed depends on how far the particle is from the midpoint it is largest at \( x = 0 \), smallest at the turning points.
Example
A particle performs SHM with displacement \( \mathrm{x = 0.10\,\sin(5t)} \). Find the expression for velocity as a function of time.
▶️ Answer / Explanation
Amplitude: \( \mathrm{x_0 = 0.10\ m} \)
Angular frequency: \( \mathrm{\omega = 5\ rad\,s^{-1}} \)
Maximum velocity:
\( \mathrm{v_0 = \omega x_0 = 5 \times 0.10 = 0.5\ m\,s^{-1}} \)
Velocity expression:
\( \mathrm{v = 0.5\,\cos(5t)} \)
Example
A particle oscillates with amplitude \( \mathrm{0.20\ m} \) and angular frequency \( \mathrm{4\ rad\,s^{-1}} \). Find the speed when the displacement is \( \mathrm{x = 0.12\ m} \).
▶️ Answer / Explanation
Use: \( \mathrm{v = \pm \omega \sqrt{x_0^2 – x^2}} \)
\( \mathrm{v = \pm 4 \sqrt{(0.20)^2 – (0.12)^2}} \)
\( \mathrm{v = \pm 4 \sqrt{0.04 – 0.0144}} = \pm 4 \sqrt{0.0256} \)
\( \mathrm{v = \pm 4(0.16) = \pm 0.64\ m\,s^{-1}} \)
Speed = \( \mathrm{0.64\ m\,s^{-1}} \)
Example
A particle obeys \( \mathrm{x = 0.15\sin(8t)} \). Find the maximum velocity and the velocity at time \( \mathrm{t = 0.10\ s} \).
▶️ Answer / Explanation
Maximum velocity:
\( \mathrm{v_0 = \omega x_0 = 8 \times 0.15 = 1.2\ m\,s^{-1}} \)
Velocity at time \( \mathrm{t = 0.10\ s} \):
\( \mathrm{v = v_0 \cos(\omega t) = 1.2\cos(8 \times 0.10)} \)
\( \mathrm{v = 1.2\cos(0.8)} \)
Numerical value:
\( \mathrm{v = 1.2 \times 0.696 = 0.835\ m\,s^{-1}} \)
Maximum velocity = \( \mathrm{1.2\ m\,s^{-1}} \)
Velocity at 0.10 s = \( \mathrm{0.84\ m\,s^{-1}} \)
Graphical Interpretation of SHM: Displacement, Velocity, and Acceleration
Simple harmonic motion (SHM) is represented by smooth sinusoidal curves. Understanding how displacement, velocity, and acceleration vary graphically is essential for analysing oscillatory systems.
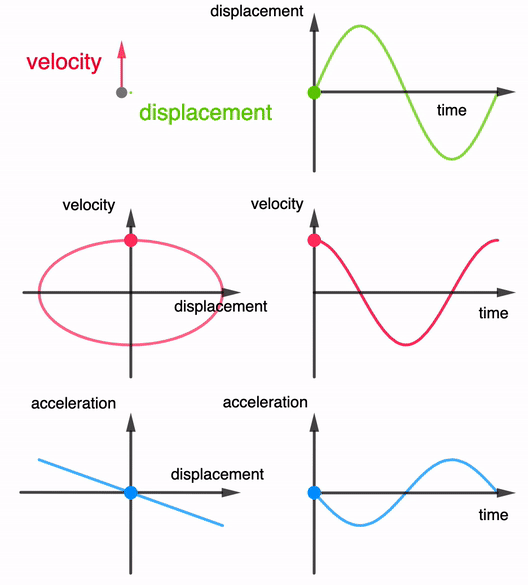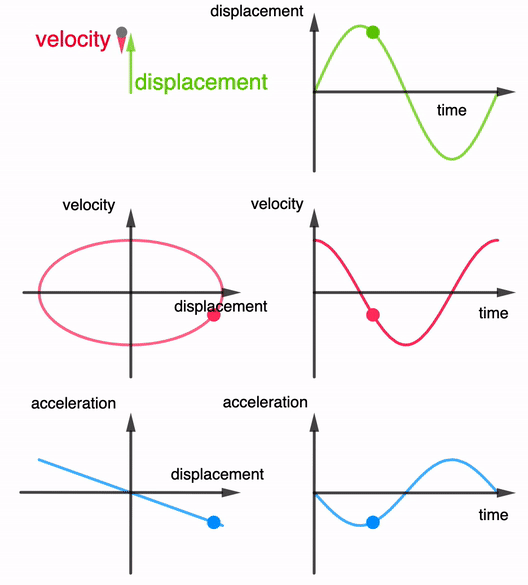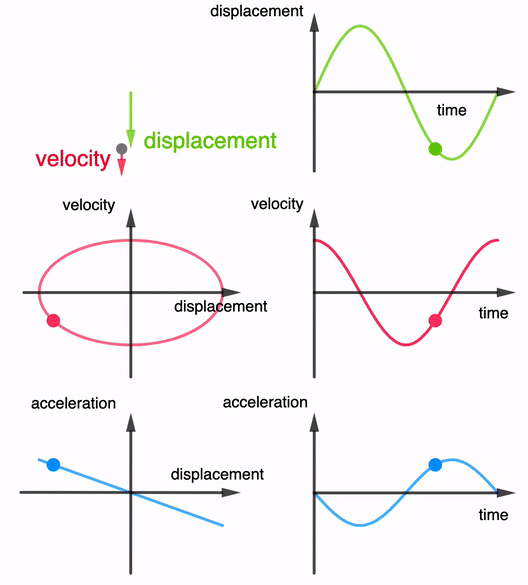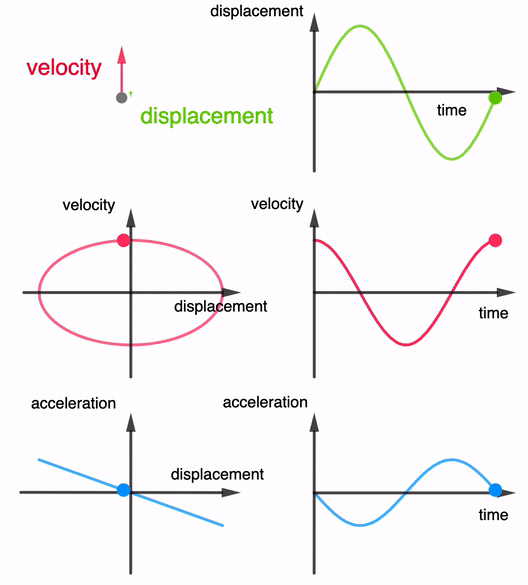
1. Displacement–Time Graph (x–t)
- A sine (or cosine) curve.
- Maximum value = \( \mathrm{x_0} \) (amplitude).
- Crosses zero at equilibrium points.
- Repeats every period \( \mathrm{T} \).
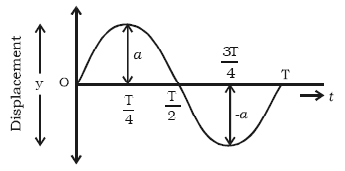
General form:
\( \mathrm{x = x_0 \sin(\omega t)} \)
2. Velocity–Time Graph (v–t)
- Also sinusoidal but shifted 90° (π/2) ahead of displacement.
- Maximum at equilibrium where displacement = 0.
- Zero at maximum displacement.
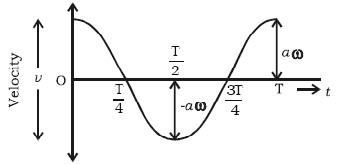
General form:
\( \mathrm{v = v_0 \cos(\omega t)} \)
3. Acceleration–Time Graph (a–t)
- Sinusoidal curve inverted relative to displacement.
- Always opposite in sign to displacement.
- Maximum magnitude at maximum displacement.
- Zero acceleration at equilibrium.
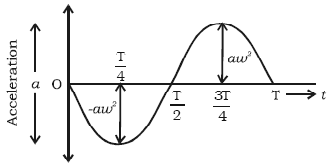
General form:
\( \mathrm{a = -\omega^2 x_0 \sin(\omega t)} \)
Key Phase Relationships:
- Velocity leads displacement by 90°.
- Acceleration leads velocity by 90°.
- Acceleration is in complete antiphase with displacement.
Graphical Summary:
- x–t: peaks at ±\( \mathrm{x_0} \)
- v–t: peaks at ±\( \mathrm{v_0 = \omega x_0} \)
- a–t: peaks at ±\( \mathrm{\omega^2 x_0} \)
Example
A displacement–time graph shows a sine wave of amplitude 0.20 m and period 4 s. State the maximum velocity and describe the velocity graph qualitatively.
▶️ Answer / Explanation
Angular frequency:
\( \mathrm{\omega = \frac{2\pi}{T} = \frac{2\pi}{4} = \frac{\pi}{2}} \)
Maximum velocity:
\( \mathrm{v_0 = \omega x_0 = \frac{\pi}{2} \times 0.20 = 0.314\ m\,s^{-1}} \)
Description of v–t graph:
- Cosine-shaped curve.
- Maxima at ±0.314 m/s.
- Crosses zero at the same times displacement is maximum.
- Leads displacement graph by 90°.
Example
The velocity–time graph of a SHM oscillator is a cosine curve with maximum value 1.5 m/s and angular frequency 6 rad/s. Sketch or describe the corresponding displacement–time graph.
▶️ Answer / Explanation
Displacement lags velocity by 90°.
Find amplitude:
\( \mathrm{x_0 = \frac{v_0}{\omega} = \frac{1.5}{6} = 0.25\ m} \)
Description of x–t graph:
- Sine wave (because v is cosine).
- Amplitude = 0.25 m.
- Crosses zero when velocity is at a maximum.
- Reaches ±0.25 m when velocity = 0.
Example
An acceleration–time graph for SHM shows a sinusoidal curve with maximum value \( \mathrm{3.6\ m\,s^{-2}} \) and angular frequency \( \mathrm{9\ rad\,s^{-1}} \). Determine the amplitude of oscillation and sketch/describe the displacement–time graph.
▶️ Answer / Explanation
Acceleration in SHM:
\( \mathrm{a_{max} = \omega^2 x_0} \)
So:
\( \mathrm{x_0 = \frac{a_{max}}{\omega^2} = \frac{3.6}{81} = 0.0444\ m} \)
Amplitude = 0.044 m
Description of x–t graph:
- Sine curve.
- Amplitude = 0.044 m.
- Antiphase with the acceleration graph (when displacement is max, acceleration is min).
- Crosses equilibrium (x = 0) when acceleration is zero.
