Electric Field Definition
An electric field is a region of space in which an electric charge “feels” a force Electric field strength at a point is defined as: The electrostatic force per unit positive charge acting on a stationary point
charge at that point Electric field strength can be calculated using the equation:
$\mathrm{E}=\frac{F}{Q}$
- Where:
- $E$ = electric field strength $\left(\mathrm{N} \mathrm{C}^{-1}\right)$
- $\mathrm{F}=$ electrostatic force on the charge (N)
- $\mathrm{Q}=$ charge $(\mathrm{C})$
- It is important to use a positive test charge in this definition, as this determines the direction of the electric field
- The electric field strength is a vector quantity, it is always directed:
- Away from a positive charge
- Towards a negative charge
- Recall that opposite charges (positive and negative) charges attract each other
- Conversely, like charges (positive and positive or negative and negative) repel each other
Worked example: Calculating particle charge
A charged particle is in an electric field with electric field strength $3.5 \times 10^4 \mathrm{~N} \mathrm{C}^{-1}$ where it experiences a force of $0.3 \mathrm{~N}$.
Calculate the charge of the particle.
Answer/Explanation
Step 1:
Write down the equation for electric field strength
$
\mathrm{E}=\frac{F}{Q}
$
Step 2:
Rearrange for charge Q
$
\mathrm{Q}=\frac{F}{E}
$
Step 3:
Substitute in values and calculate
$
Q=\frac{0.3}{3.5 \times 10^4}=8.571 \times 10^{-6} \mathrm{C}=8.6 \times 10^{-6} C(2 \mathrm{~s} . \mathrm{f})
$
- Forces on Charges
The electric field strength equation can be rearranged for the force $F$ on a charge $Q$ in an electric field $E$ :
$
\mathbf{F}=\mathbf{Q E}
$
- Where:
- $\mathrm{F}=$ electrostatic force on the charge (N)
- $\mathrm{Q}=$ charge $(\mathrm{C})$
- $E$ = electric field strength $\left(\mathrm{N}^{-1}\right)$
- The direction of the force is determined by the charge:
- If the charge is positive $(+)$ the force is in the same direction as the $E$ field
- If the charge is negative (-) the force is in the opposite direction to the $E$ field
- The force on the charge will cause the charged particle to accelerate if its in the same direction as the E field, or decelerate if in the opposite
- Note: the force will always be parallel to the electric field lines
Worked example: Electric force
An electron is stationary in an electric field which has an electric field strength of $5000 \mathrm{~N} \mathrm{C}^{-1}$. Calculate the magnitude of the electric force that acts on the electron and state which direction the force will act in relation to the electric field. Electron charge $e=1.60 \times 10^{-19} \mathrm{C}$
Answer/Explanation
Step 1: Write out the equation for the force on a charged particle
$
\mathbf{F}=\mathbf{Q E}
$
Step 2: $\quad$ Substitute in values
$
F=\left(1.60 \times 10^{-19}\right) \times 5000=8 \times 10^{-16} \mathrm{~N}
$
Step 3: State the direction of the force
Since the charge is negative, the force is directed against the electric field lines and decelerates the electron.
Point Charge Approximation
- For a point outside a spherical conductor, the charge of the sphere may be considered to be a point charge at its centre
- A uniform spherical conductor is one where its charge is distributed evenly
- The electric field lines around a spherical conductor are therefore identical to those around a point charge
- An example of a spherical conductor is a charged sphere
- The field lines are radial and their direction depends on the charge of the sphere
- If the spherical conductor is positively charged, the field lines are directed away from the centre of the sphere
- If the spherical conductor is negatively charged, the field lines are directed towards the centre of the sphere
Exam Tip
You might have noticed that the electric fields share many similarities to the gravitational fields. The main difference being the gravitational force is always attractive, whilst electrostatic forces can be attractive or repulsive. You should make a list of all the similarities and differences you can find, as this could come up in an exam question.
Representing Electric Fields
- The direction of electric fields is represented by electric field lines
- Electric field lines are directed from positive to negative
- Therefore, the field lines must be pointed away from the positive charge and towards the negative charge
- A radial field spreads uniformly to or from the charge in all directions
- e.g. the field around a point charge or sphere
- Around a point charge, the electric field lines are directly radially inwards or outwards:
- If the charge is positive $(+)$, the field lines are radially outwards
- If the charge is negative (-), the field lines are radially inwards
- A uniform electric field has the same electric field strength throughout the field
- For example, the field between oppositely charged parallel plates
- This is represented by equally spaced field lines
- This shares many similarities to radial gravitational field lines around a point mass
- Since gravity is only an attractive force, the field lines will look similar to the negative point charge, whilst electric field lines can be in either direction
- A non-uniform electric field has varying electric field strength throughout
- The strength of an electric field is determined by the spacing of the field lines:
- A stronger field is represented by the field lines closer together
- A weaker field is represented by the field lines further apart
- The electric field lines are directed from the positive to the negative plate
- A radial field is considered a non-uniform field
- So, the electric field strength $E$ is different depending on how far you are from a charged particle
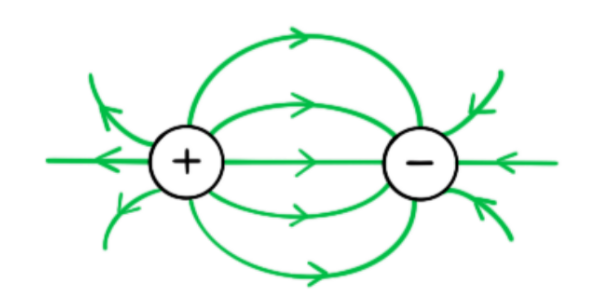
Worked example
Sketch the electric field lines between the two point charges in the diagram below.

Answer/Explanation
Electric field lines around point charges are radially outwards for positive charges and radially inwards for negative charges The field lines must be drawn with arrows from the positive charge to the negative charge
Exam Tip
Always label the arrows on the field lines! The lines must also touch the surface of the source charge or plates.
