Electric Field of a Point Charge
- The electric field strength at a point describes how strong or weak an electric field is at that point
- The electric field strength $E$ at a distance $r$ due to a point charge $Q$ in free space is defined by:
$
E=\frac{Q}{4 \pi \varepsilon_0 r^2}
$
- Where:
- $Q=$ the charge producing the electric field (C)
- $r=$ distance from the centre of the charge $(m)$
- $\varepsilon_0=$ permittivity of free space $\left(\mathrm{F} \mathrm{m}^{-1}\right)$
- This equation shows:
- Electric field strength is not constant
- As electric field strength increases, decreases by a factor of $1 / r^2$
- This is an inverse square law relationship with distance
- This means the field strength decreases by a factor of four when the distance is doubled
- Note: this equation is only for the field strength around a point charge since it produces a radial field
- The electric field strength is a vector Its direction is the same as the electric field lines
- If the charge is negative, the $E$ field strength is negative and points towards the centre of the charge
- If the charge is positive, the E field strength is positive and points away from the centre of the charge
- This equation is analogous to the gravitational field strength around a point mass
Worked example: Surface charge of a sphere
A metal sphere of diameter $15 \mathrm{~cm}$ is negatively charged. The electric field strength at the surface of the sphere is $1.5 \times 10^5 \mathrm{~V} \mathrm{~m}$.- Determine the total surface charge of the sphere.
Answer/Explanation
Step 1:
Write down the known values
Electric field strength, $\mathrm{E}=1.5 \times 10^5 \mathrm{~V} \mathrm{~m}^{-1}$
Radius of sphere, $r=15 / 2=7.5 \mathrm{~cm}=7.5 \times 10^{-2} \mathrm{~m}$
Step 2:
Write out the equation for electric field strength
$
\mathrm{E}=\frac{Q}{4 \pi \varepsilon_0 r^2}
$
Step 3:
Rearrange for charge Q
$
Q=4 \pi \varepsilon E^2 r^2
$
Step 4: $\quad$ Substitute in values
$
Q=\left(4 \pi \times 8.85 \times 10^{-12}\right) \times\left(1.5 \times 10^5\right) \times\left(7.5 \times 10^{-2}\right)^2=9.38 \times 10^{-8} \mathrm{C}=94 \mathrm{nC}(2 \mathrm{s.f})
$
Exam Tip
Remember to always square the distance!
Motion of Charged Particles
- A charged particle in an electric field will experience a force on it that will cause it to move
- If a charged particle remains still in a uniform electric field, it will move parallel to the electric field lines (along or against the field lines depending on its charge)
- If a charged particle is in motion through a uniform electric field (e.g. between two charged parallel plates), it will experience a constant electric force and travel in a parabolic trajectory
- The direction of the parabola will depend on the charge of the particle
- A positive charge will be deflected towards the negative plate
- A negative charge will be deflected towards the positive plate
- The force on the particle is the same at all points and is always in the same direction
- Note: an uncharged particle, such as a neutron experiences no force in an electric field and will therefore travel straight through the plates undeflected
- The amount of deflection depends on the following properties of the particles:
- Mass – the greater the mass, the smaller the deflection and vice versa
- Charge – the greater the magnitude of the charge of the particle, the greater the deflection and vice versa
- Speed – the greater the speed of the particle, the smaller the deflection and vice versa
Worked example
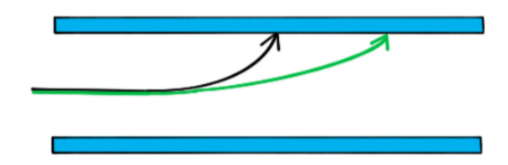
A single proton travelling with a constant horizontal velocity enters a uniform electric field between two parallel charged plates. The diagram shows the path taken by the proton.
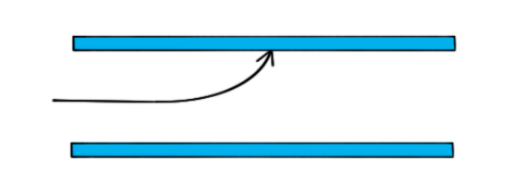
Draw the path taken by a boron nucleus that enters the electric field at the same point and with the same velocity as the proton.
Atomic number of boron $=5$
Mass number of boron $=11$
Answer/Explanation
Step 1:
Compare the charge of the boron nucleus to the proton
- Boron has 5 protons, meaning it has a charge $5 \times$ greater than the proton
- The force on boron will therefore be $5 \times$ greater than on the proton
Step 2:
Compare the mass of the boron nucleus to the proton
- The boron nucleus has a mass of 11 nucleons meaning its mass is $11 \times$ greater than the proton
- The boron nucleus will therefore be less deflected than the proton
Step 3:
Draw the trajectory of the boron nucleus
- Since the mass comparison is much greater than the charge comparison, the boron nucleus will be much less deflected than the proton
- The nucleus is positively charged since the neutrons in the nucleus have no charge
- Therefore, the shape of the path will be the same as the proton