CIE AS/A Level Physics 19.3 Discharging a capacitor Study Notes- 2025-2027 Syllabus
CIE AS/A Level Physics 19.3 Discharging a capacitor Study Notes – New Syllabus
CIE AS/A Level Physics 19.3 Discharging a capacitor Study Notes at IITian Academy focus on specific topic and type of questions asked in actual exam. Study Notes focus on AS/A Level Physics latest syllabus with Candidates should be able to:
- analyse graphs of the variation with time of potential difference, charge and current for a capacitor discharging through a resistor
- recall and use τ = RC for the time constant for a capacitor discharging through a resistor
- use equations of the form x = x0 e–(t / RC) where x could represent current, charge or potential difference for a capacitor discharging through a resistor
Graphs of Potential Difference, Charge, and Current During Capacitor Discharge
When a capacitor discharges through a resistor, all measurable quantities—potential difference, charge, and current—decrease exponentially with time. These quantities follow smooth curves that fall rapidly at first and then level off gradually.
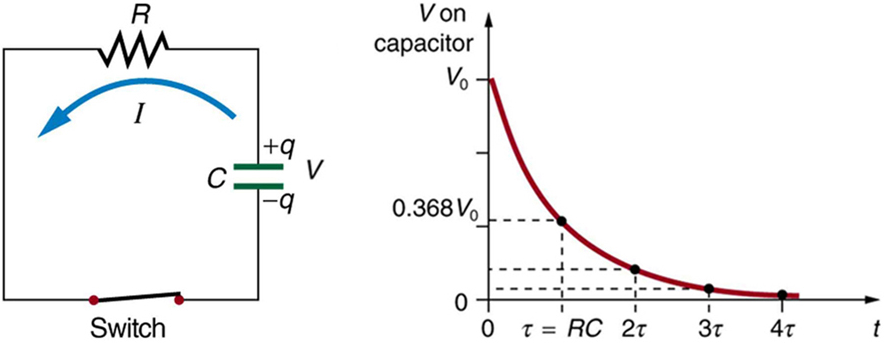
A discharging capacitor obeys exponential decay.
General Behavior:
- At \( \mathrm{t = 0} \): values start at maximum (initially charged capacitor).
- As time increases: all quantities decrease smoothly.
- As \( \mathrm{t \to \infty} \): quantities approach 0 but never instantly reach zero.
- The rate of decrease depends on the time constant \( \mathrm{\tau = RC} \).
Mathematical Forms of Decay:
- Charge: \( \mathrm{Q(t) = Q_0 e^{-t/RC}} \)
- Potential difference: \( \mathrm{V(t) = V_0 e^{-t/RC}} \)
- Current: \( \mathrm{I(t) = I_0 e^{-t/RC}} \) (and always negative in direction of discharge)
All three graphs have the same shape: an exponential decay curve with an initially steep slope.
Graph Interpretation:
- Initial slope: steep → rapid drop in values.
- Later slope: flatter → slow approach to zero.
- Current graph: often shown entirely below zero (negative direction), but magnitude still decays exponentially.
Example
On a graph of charge vs time for a discharging capacitor, the charge decreases quickly at first and then slowly approaches zero. Explain why the curve looks like this.
▶️ Answer / Explanation
At the start, the capacitor has a large initial charge and therefore a large potential difference. This produces a large current, so charge leaves quickly → steep slope.
As the capacitor discharges, both the charge and potential difference decrease. The current becomes smaller, so charge leaves more slowly → curve flattens.
This results in an exponential decay curve.
Example
A graph shows that the potential difference across a discharging capacitor falls from 8.0 V to 3.0 V in 4.0 s. Explain whether the discharge is linear or exponential.
▶️ Answer / Explanation
The drop in voltage is not uniform per unit time—a linear discharge would show a straight-line decrease.
Instead, the initial drop is steep (8.0 V → 3.0 V quickly), but later the voltage decreases slowly. This indicates exponential decay, consistent with:
\( \mathrm{V(t) = V_0 e^{-t/RC}} \)
Thus, the discharge is exponential, not linear.
Example
A discharging capacitor has an initial current of 40 mA. After one time constant \( \mathrm{\tau = RC} \), the graph shows that the current has dropped to 14.7 mA. Use the graph behaviour to justify that this follows exponential decay.
▶️ Answer / Explanation
For exponential decay, after one time constant:
\( \mathrm{I = I_0 e^{-1}} \approx 0.37 I_0 \)
Calculate expected current:
\( \mathrm{I = 0.37 \times 40\ mA = 14.8\ mA} \)
The graph shows 14.7 mA — very close to the theoretical exponential result.
This confirms that the current decreases according to the exponential law:
\( \mathrm{I(t) = I_0 e^{-t/RC}} \)
Time Constant for a Discharging Capacitor: \( \mathrm{\tau = RC} \)
The time constant of a capacitor–resistor (RC) circuit determines how quickly a capacitor discharges (or charges). It is a measure of how long it takes for the charge, current, or potential difference to fall to about 37% of its initial value during discharge.
Definition:![]()
\( \mathrm{\tau = RC} \)
- \( \mathrm{\tau} \) = time constant (s)
- \( \mathrm{R} \) = resistance (Ω)
- \( \mathrm{C} \) = capacitance (F)
Meaning of the Time Constant:
- After time \( \mathrm{\tau} \), the charge, voltage, or current falls to: \( \mathrm{0.37\ (37\%)} \) of its initial value.
- After \( \mathrm{5\tau} \), the capacitor is considered fully discharged (less than 1% remains).
- A large \( \mathrm{R} \) or large \( \mathrm{C} \) → slow discharge (large \( \mathrm{\tau} \)).
- A small \( \mathrm{R} \) or small \( \mathrm{C} \) → fast discharge (small \( \mathrm{\tau} \)).
Exponential Relationship:
- \( \mathrm{Q(t) = Q_0 e^{-t/\tau}} \)
- \( \mathrm{V(t) = V_0 e^{-t/\tau}} \)
- \( \mathrm{I(t) = I_0 e^{-t/\tau}} \)
Example
A capacitor of \( \mathrm{50\ \mu F} \) discharges through a \( \mathrm{2000\ \Omega} \) resistor. Calculate the time constant.
▶️ Answer / Explanation
Convert capacitance:
\( \mathrm{50\ \mu F = 50\times10^{-6}\ F} \)
Use:
\( \mathrm{\tau = RC = (2000)(50\times10^{-6})} \)
\( \mathrm{\tau = 0.10\ s} \)
Time constant = 0.10 s
Example
A capacitor discharges through a resistor, and after 0.50 s the potential difference has fallen to 37% of its initial value. Find the time constant \( \mathrm{\tau} \).
▶️ Answer / Explanation
By definition:
At \( \mathrm{t = \tau} \), \( \mathrm{V = 0.37V_0} \).
The graph shows this at 0.50 s → therefore:
\( \mathrm{\tau = 0.50\ s} \)
Time constant = 0.50 s
Example
A 120 μF capacitor is discharged through a resistor. The initial current is \( \mathrm{I_0 = 45\ mA} \). After 0.30 s, the current drops to \( \mathrm{I = 15\ mA} \). Using the exponential decay law, determine the resistance R.
▶️ Answer / Explanation
Decay law:
\( \mathrm{I = I_0 e^{-t/\tau}} \)
Substitute values:
\( \mathrm{15 = 45 e^{-0.30/\tau}} \)
Divide both sides:
\( \mathrm{\frac{1}{3} = e^{-0.30/\tau}} \)
Take natural log:
\( \mathrm{\ln\left(\frac{1}{3}\right) = -0.30/\tau} \)
\( \mathrm{-1.099 = -0.30/\tau} \)
Thus:
\( \mathrm{\tau = \frac{0.30}{1.099} = 0.273\ s} \)
Now use \( \mathrm{\tau = RC} \):
\( \mathrm{R = \frac{\tau}{C} = \frac{0.273}{120\times10^{-6}}} \)
\( \mathrm{R = 2275\ \Omega} \)
Resistance ≈ \( \mathrm{2.3\ k\Omega} \)
Exponential Decay in a Discharging Capacitor
When a capacitor discharges through a resistor, all measurable quantities—charge, current, and potential difference—decrease exponentially with time.
General Exponential Decay Equation:![]()
\( \mathrm{x = x_0\, e^{-t/RC}} \)
- \( \mathrm{x} \) = value at time \( \mathrm{t} \) (could be \( \mathrm{Q} \), \( \mathrm{V} \), or \( \mathrm{I} \))
- \( \mathrm{x_0} \) = initial value at \( \mathrm{t = 0} \)
- \( \mathrm{R} \) = resistance (Ω)
- \( \mathrm{C} \) = capacitance (F)
- \( \mathrm{RC} \) = time constant \( \mathrm{\tau} \)
The same formula applies to:
- Charge: \( \mathrm{Q(t) = Q_0 e^{-t/RC}} \)
- Voltage: \( \mathrm{V(t) = V_0 e^{-t/RC}} \)
- Current: \( \mathrm{I(t) = I_0 e^{-t/RC}} \)
All three decay exponentially at the same rate.
Meaning of the Exponential:
- After one time constant \( \mathrm{\tau = RC} \), the quantity falls to about 37% of its initial value.
- The decay is fast at first, then becomes slow.
Example
A capacitor discharges from an initial voltage of 10 V. After one time constant \( \mathrm{\tau} \), what is the voltage?
▶️ Answer / Explanation
Use:
\( \mathrm{V = V_0 e^{-t/RC}} \)
At \( \mathrm{t = RC = \tau} \):
\( \mathrm{V = 10 e^{-1} = 10(0.37) = 3.7\ V} \)
Voltage after one time constant = 3.7 V
Example
A capacitor with \( \mathrm{\tau = 0.40\ s} \) initially stores a charge of \( \mathrm{Q_0 = 5.0\times10^{-6}\ C} \). Find the charge remaining after 1.2 s.
▶️ Answer / Explanation
Use \( \mathrm{Q = Q_0 e^{-t/\tau}} \):
\( \mathrm{Q = (5.0\times10^{-6}) e^{-1.2/0.40}} \)
\( \mathrm{Q = 5.0\times10^{-6} \cdot e^{-3}} \)
\( \mathrm{e^{-3} = 0.0498} \)
\( \mathrm{Q = 2.49\times10^{-7}\ C} \)
Charge remaining = \( \mathrm{2.5\times10^{-7}\ C} \)
Example
A capacitor discharges through a resistor. The initial current is \( \mathrm{I_0 = 60\ mA} \). After 0.50 s, the current is \( \mathrm{I = 12\ mA} \). Determine the time constant \( \mathrm{\tau} \).
▶️ Answer / Explanation
Use the decay equation:
\( \mathrm{I = I_0 e^{-t/\tau}} \)
Substitute values:
\( \mathrm{12 = 60 e^{-0.50/\tau}} \)
Divide both sides:
\( \mathrm{\frac{1}{5} = e^{-0.50/\tau}} \)
Take natural log:
\( \mathrm{\ln\left(\frac{1}{5}\right) = -0.50/\tau} \)
\( \mathrm{-1.609 = -0.50/\tau} \)
Thus:
\( \mathrm{\tau = \dfrac{0.50}{1.609} = 0.31\ s} \)
Time constant = 0.31 s
