FORCE ON A MOVING CHARGE
Calculating Magnetic Force on a Moving Charge
- The magnetic force on an isolating moving charge, such an electron, is given by the equation:
$
F=B Q v \sin \theta
$
- Where:
- $\mathrm{F}=$ force on the charge $(N)$
- $B=$ magnetic flux density $(T)$
- $v=$ speed of the charge $\left(\mathrm{m} \mathrm{s}^{-1}\right)$
- $\theta=$ angle between charge’s velocity and magnetic field (degrees)
- Equivalent to the force on a wire, if the magnetic field $B$ is perpendicular to the direction of the charge’s velocity, the equation simplifies to:
$
\mathbf{F}=\mathbf{B Q v}
$
- According to Fleming’s left hand rule:
- When an electron enters a magnetic field from the left, if the magnetic field is directed into the page, then the force on it will be directed upwards
- The equation shows:
- If the direction of the electron changes, the magnitude of the force will change too
- The force due to the magnetic field is always perpendicular to the velocity of the electron
- Note: this is equivalent to circular motion
- Fleming’s left-hand rule can be used again to find the direction of the force, magnetic field and velocity
- The key difference is that the second finger representing current I (direction of positive charge) is now the direction of velocity $\boldsymbol{v}$ of the positive charge
Worked example: Calculating magnetic force on a moving electron
An electron is moving at $5.3 \times 10^7 \mathrm{~m} \mathrm{~s}^{-1}$ in a uniform magnetic field of flux density $0.2 \mathrm{~T}$. Calculate the force on the electron when it is moving at $30^{\circ}$ to the field, and state the factor it increases by compared to when it travels perpendicular to the field.
Answer/Explanation
Step 1:
Write out the known quantities
Speed of the electron, $v=5.3 \times 10^7 \mathrm{~m} \mathrm{~s}^{-1}$
Charge of an electron, $Q=1.60 \times 10^{-19} \mathrm{C}$
Magnetic flux density, $B=0.2 \mathrm{~T}$
Angle between electron and magnetic field, $\theta=30^{\circ}$
Step 2: Write down the equation for the magnetic force on an isolated particle
$
F=B Q v \sin \theta
$
Step 3: Substitute in values, and calculate the force on the electron at $30^{\circ}$
$
F=(0.2) \times\left(1.60 \times 10^{-19}\right) \times\left(5.3 \times 10^7\right) \times \sin (30)=8.5 \times 10^{-13} \mathrm{~N}
$
Step 4: $\quad$ Calculate the electron force when travelling perpendicular to the field
$
F=B Q v=(0.2) \times\left(1.60 \times 10^{-19}\right) \times\left(5.3 \times 10^7\right)=1.696 \times 10^{-12} \mathrm{~N}
$
Step 5: Calculate the ratio of the perpendicular force to the force at $30^{\circ}$
$
\frac{1.696 \times 10^{-12}}{8.5 \times 10^{-13}}=1.995=2
$
Therefore, the force on the electron is twice as strong when it is moving perpendicular to the field than when it is moving at 30o to the field
Exam Tip
Remember not to $\mathrm{mix}$ this up with $\mathrm{F}=$ BIL!
- $\mathbf{F}=\mathbf{B I L}$ is for a current carrying conductor
- $\mathbf{F}=\mathbf{B q v}$ is for an isolated moving charge (which may be inside a conductor)
HALL VOLTAGE
- The Hall voltage is a product of the Hall effect
- Hall voltage is defined as:
The potential difference produced across an electrical conductor when an external magnetic field is applied perpendicular to the current through the conductor - When an external magnetic field is applied perpendicular to the direction of current through a conductor, the electrons experience a magnetic force
- This makes them drift to one side of the conductor, where they all gather and becomes more negatively charged
- This leaves the opposite side deficident of electrons, or positively charged
- There is now a potential difference across the conductor
- This is called the Hall Voltage, $V_{\mathrm{H}}$
- An equation for the Hall voltage $V_{\mathrm{H}}$ is derived from the electric and magnetic forces on the charges
- The voltage arises from the electrons accumulating on one side of the conductor slice
- As a result, an electric field is set up between the two opposite sides
- The two sides can be treated like oppositely charged parallel plates, where the electric field strength $E$ is equal to:
$
\mathrm{E}=\frac{V_H}{d}
$
- Where:
- $V_H=$ Hall voltage $(\mathrm{V})$
- $d=$ width of the conductor slice (m)
- A single electron has a drift velocity of $v$ within the conductor. The magnetic field is into the plane of the page, therefore the electron has a magnetic force $F_B$ to the right:
$
\mathrm{F}_{\mathrm{B}}=\mathbf{B q v}
$
- This is equal to the electric force $F_E$ to the left:
$
\begin{aligned}
F_E & =q E \\
q E & =B q v
\end{aligned}
$
- Substituting $E$ and cancelling the charge $q$
$
\frac{V_H}{d}=\mathrm{Bv}
$
- Recall that current $I$ is related to the drift velocity $v$ by the equation:
$
\mathbf{I}=\mathbf{n A v q}
$
- Where:
- $A=$ cross-sectional area of the conductor $\left(\mathrm{m}^2\right)$
- $\mathrm{n}=$ number density of electrons $\left(m^{-3}\right)$
- Rearranging this for $v$ and substituting it into the equation gives:
$
\frac{V_H}{d}=\mathrm{B} \frac{I}{n A q}
$
- The cross-sectional area $A$ of the slice is the product of the width $d$ and thickness $t$ :
$
\mathbf{A}=\mathbf{d t}
$
- Substituting $A$ and rearranging for the Hall voltage $V_{\mathrm{H}}$ leads to the equation:
$
\frac{V_H}{d}=\mathrm{B} \frac{I}{n(d t) q}
$
$
\mathrm{V}_{\mathrm{H}}=\mathrm{B} \frac{I}{n t q}
$
- Where:
- $B=$ magnetic flux density $(T)$
- $q=$ charge of the electron (C)
- $I=$ current $(A)$
- $\mathrm{n}=$ number density of electrons $\left(\mathrm{m}^{-3}\right)$
- $\mathrm{t}=$ thickness of the conductor $(\mathrm{m})$
- This equation shows that the smaller the electron density $n$ of a material, the larger the magnitude of the Hall voltage
- This is why a semiconducting material is often used for a Hall probe
- Note: if the electrons were placed by positive charge carriers, the negative and positive charges would still deflect in opposite directions
- This means there would be no change in the polarity (direction) of the Hall voltage
Exam Tip
Remember to use Fleming’s left-hand rule to obtain the direction the electrons move due to the magnetic force created by the magnetic field.
USING A HALL PROBE
Measuring Magnetic Flux Density using a Hall Probe
- A Hall probe can be used to measure the magnetic flux density between two magnets based on the Hall effect
- It consists of a cylinder with a flat surface at the end
- To measure the magnetic flux density between two magnets, the flat surface of the probe must be directed between the magnets so the magnetic field lines pass completely perpendicular to this surface
- The probe is connected to a voltmeter to measure the Hall voltage
- If the probe is not held in the correct orientation (perpendicular to the field lines), the voltmeter reading will be reduced
- Since the Hall voltage is directly proportional to the magnetic flux density, the flux density of the magnets can be obtained
- A Hall probe is sensitive enough to measure even the Earth’s magnetic flux density
Worked example: Using a Hall probe
A Hall probe is placed near one end of a solenoid, as shown in the diagram.
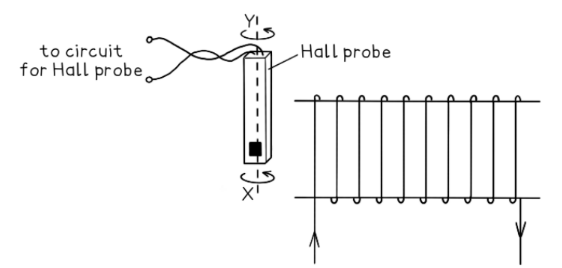
The Hall probe is rotated about the axis $X Y$.
State and explain why the magnitude of the Hall voltage varies.
- The Hall voltage depends on angle between the magnetic field and the plane of the probe
- The Hall voltage reaches a maximum when the field is perpendicular to the probe
- The Hall voltage is zero when the field is parallel to the probe
MOTION OF A CHARGED PARTICLE IN A MAGNETIC FIELD
Motion of a Charged Particle in a Uniform Magnetic Field
- A charged particle in uniform magnetic field which is perpendicular to its direction of motion travels in a circular path
- This is because the magnetic force $F_{\mathrm{B}}$ will always be perpendicular to its velocity $v$
- $F_{\mathrm{B}}$ will always be directed towards the centre of the path
- The magnetic force $F_8$ provides the centripetal force on the particle
- Recall the equation for centripetal force:
$
\mathrm{F}=\frac{m v^2}{r}
$
- Where:
- $\mathrm{m}=$ mass of the particle $(\mathrm{kg})$
- $v=$ linear velocity of the particle $\left(\mathrm{m} \mathrm{s}^{-1}\right)$
- $r=$ radius of the orbit $(\mathrm{m})$
- Equating this to the force on a moving charged particle gives the equation:
$
\frac{m v^2}{r}=\mathrm{Bqv}
$
- Rearranging for the radius $r$ obtains the equation for the radius of the orbit of a charged particle in a perpendicular magnetic field:
$
r=\frac{m v}{B q}
$
- This equations shows that:
- Faster moving particles with speed $v$ move in larger circles (larger $r$ ): $\mathbf{r} \propto \mathbf{v}$
- Particles with greater mass $m$ move in larger circles: $\mathbf{r} \propto \mathbf{m}$
- Particles with greater charge $q$ move in smaller circles: $\mathbf{r} \propto 1 / \mathbf{q}$
- Particles moving in a strong magnetic field $B$ move in smaller circles: $\mathbf{r} \propto 1$ / B
Worked example: Calculating the radius of motion
An electron with a charge-to-mass ratio of $1.8 \times 10^{11} \mathrm{C} \mathrm{kg}^{-1}$ is travelling at right angles to a uniform magnetic field of flux density $6.2 \mathrm{mT}$.
The speed of the electron is $3.0 \times 10^6 \mathrm{~m} \mathrm{~s}^{-1}$.
Calculate the radius of the circular path of the electron.
Answer/Explanation
Step 1:
Write down the known quantities
Charge-to-mass ratio $=\frac{q}{m}=1.8 \times 10^{11} \mathrm{C} \mathrm{kg}^{-1}$
Magnetic flux density, $B=6.2 \mathrm{mT}$
Electron speed, $\mathrm{v}=3.0 \times 10^6 \mathrm{~m} \mathrm{~s}^{-1}$
Step 2: Write down the equation for the radius of a charged particle in a perpendicular magnetic field
$
\mathrm{r}=\frac{m v}{B q}
$
Step 3:
Substitute in values
$
\begin{gathered}
\frac{m}{q}=\frac{1}{1.8 \times 10^{11}} \\
r=\frac{\left(3.0 \times 10^6\right)}{\left(1.8 \times 10^{11}\right)\left(6.2 \times 10^{-3}\right)}=2.688 \times 10^{-3} \mathrm{~m}=2.7 \mathrm{~mm} \text { (2 s.f.) }
\end{gathered}
$
VELOCITY SELECTION
Velocity Selection
- A velocity selector is:
A device consisting of perpendicular electric and magnetic fields where charged particles with a specific velocity can be filtered - Velocity selectors are used in devices, such as mass spectrometers, in order to produce a beam of charged particles all travelling at the same velocity
- The construction of a velocity selector consists of two horizontal oppositely charged plates situated in a vacuum chamber
- The plates provide a uniform electric field with strength $E$ between them
- There is also a uniform magnetic field with flux density $B$ applied perpendicular to the electric field
- If a beam of charged particles enter between the plates, they may all have the same charge but travel at different speeds $v$
- The electric force does not depend on the velocity: $F_E=E Q$
- However, the magnetic force does depend on the velocity: $F_B=B Q v$
- The magnetic force will be greater for particles which are travelling faster
- To select particles travelling at exactly the desired the speed $v$, the electric and magnetic force must therefore be equal, but in opposite directions
$
F_E=F_B
$
- The resultant force on the particles at speed $v$ will be zero, so they will remain undeflected and pass straight through between the plates
- By equating the electric and magnetic force equations:
$
E Q=B Q v
$
- The charge $Q$ will cancel out on both sides to give the selected velocity $v$ equation:
$
\mathrm{v}=\frac{E}{B}
$
- Therefore, the speed $v$ in which a particle will remain undeflected is found by the ratio of the electric and magnetic field strength
- If a particle has a speed greater or less than $v$, the magnetic force will deflect it and collide with one of the charged plates
- This would remove the particles in the beam that are not exactly at speed $v$
- Note: the gravitational force on the charged particles will be negligible compared to the electric and magnetic forces and therefore can be ignored in these calculations
Worked example: Velocity selection
A positive ion travels between two charged plates towards a slit, as shown in the diagram.
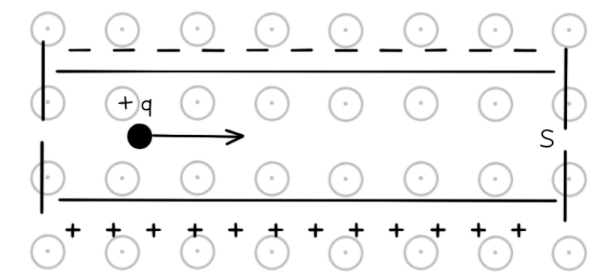
a) State the direction of the electric and magnetic fields on the ion.
b) Calculate the speed of the ion emerging from slit $\mathrm{S}$ when the magnetic flux density is $0.50 \mathrm{~T}$ and the electric field strength is $2.8 \mathrm{kV} \mathrm{m}^{-1}$.
c) Which plate will the ion be deflected towards if the speed of the ion is greater than the speed in part (b).
Part (a)
Step 1: Direction of $E$ field
- Electric field lines point from the positive to negative to charge
- Therefore, it must be directed vertically upwards
Step 2: $\quad$ Direction of B field
- Using Fleming’s left-hand rule:
- The charge or current $I$ is to the right
- $B$ is out of the page
- Therefore, the force $F$ is vertically downwards
Part (b)
Velocity selector equation
Electric field strength, $E=2.8 \mathrm{kV} \mathrm{m}^{-1}=\mathbf{2 . 8} \times 10^3 \mathrm{~V} \mathrm{~m}^{-1}$
Magnetic flux density, $B=\mathbf{0 . 5 0} \mathbf{T}$
$
\mathrm{v}=\frac{E}{B}=\frac{2.8 \times 10^3}{0.50}=5600 \mathrm{~ms}^{-1}
$
Part (c)
If the speed increases, the magnetic force must be greater because $F_B \propto v$
Since the magnetic force would direct the ion downwards in the direction of the field, the ion will be deflected towards the positive plate
