PROPERTIES AND USES OF ALTERNATING CURRENT
- An alternating current (a.c) is defined as:
A current which periodically varies from positive to negative and changes its magnitude continuously with time - This means the direction of an alternating current varies every half cycle
- The variation of current, or p.d., with time can be described as a sine curve ie. sinusoidal
- Therefore, the electrons in a wire carrying a.c. move back and forth with simple harmonic motion
- As with SHM, the relationship between time period T and frequency $f$ of an alternating current is given by:
$
\mathrm{T}=\frac{1}{f}
$
- Peak current $\left(I_0\right)$, or peak voltage $\left(V_0\right)$, is defined as:
The maximum value of the alternating current or voltage - Peak current, or voltage, can be determined from the amplitude of the graph
- Mains electricity is supplied as alternating current
- Power stations produce alternating current
- This is the type of current supplied when devices are plugged into sockets
Worked example: Calculating frequency
The variation with time $t$ of the output voltage $V$ of an alternating voltage supply is shown in the graph below.
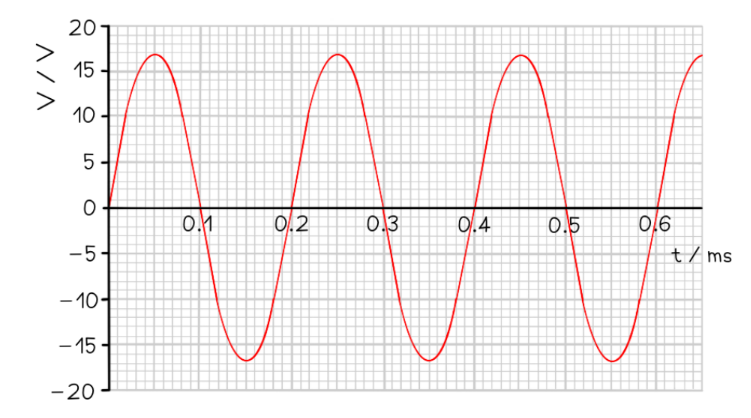
Use the graph to calculate the frequency of the supply.
Answer/Explanation
Step 1:
Write down the period-frequency relation
$
\mathrm{f}=\frac{1}{T}
$
Step 2:
Calculate the time period from the graph
- The time period is the time taken for one complete cycle
- From the graph this is equation to $0.2 \mathrm{~ms}$
- Therefore, the time period, $\mathrm{T}=0.2 \mathrm{~ms}=\mathbf{0 . 2} \times 10^{-3} \mathrm{~s}$
Step 3:
Substitute into frequency equation
$
f=\frac{1}{0.2 \times 10^{-3}}=5000 \mathrm{~Hz}=5 \mathrm{kHz}
$
Exam Tip
Remember to double check the units on the alternating current and voltage graphs. These are often shown in the range of milli-seconds (ms) instead of seconds (s) on the $x$ axis.
Using Sinusoidal Representations
- The equation representing alternating current which gives the value of the current $I$ at any time $t$ is:
$
I=I_0 \sin (\omega t)
$
- Where:
- $\mathrm{I}=$ current $(\mathrm{A})$
- $\mathrm{I}_0=$ peak current $(\mathrm{A})$
- $\omega=$ angular frequency of the supply $\left(\mathrm{rad} \mathrm{s}^{-1}\right)$
- $\mathrm{t}=$ time (s)
- Note: this a sine function since the alternative current graph is sinusoidal
- A similar equation can be used for representing alternating voltage:
$
V=V_0 \sin (\omega t)
$
- Where:
- $\mathrm{V}=$ voltage $(\mathrm{V})$
- $\mathrm{V}_0=$ peak voltage $(\mathrm{V})$
- Recall the relation the equation for angular frequency $\omega$ :
$
\omega=\frac{2 \pi}{T}=2 \pi f
$
Worked example: Using sinusoidal representations
An alternating current I varies with time $t$ as shown in the graph below.
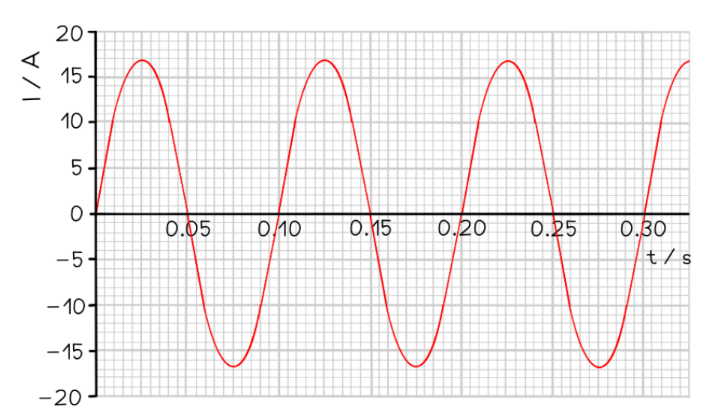
Using the graph and the equation for alternating current, calculate the value of the current at a time $0.48 \mathrm{~s}$.
Step 1: $\quad$ Write out the equation for alternating current
$
I=I_0 \sin (\omega t)
$
Step 2:
Write out the equation for angular frequency
$
\omega=\frac{2 \pi}{T}
$
Step 3:
$\quad$ Measure the time period $T$ and peak current $I_0$ from the graph
The time period is the time taken for one full cycle, $T=0.10 \mathrm{~s}$
Peak current (amplitude), $I_0=17$ A
Step 4:
Substitute values into alternating current equation at time $t$
Using the time given in the question, $t=0.48 \mathrm{~s}$
$
\mathrm{I}=\mathrm{I}_0 \sin (\omega \mathrm{t})=\mathrm{I}_0 \sin \left(\frac{2 \pi t}{T}\right)
$
$
I=17 \sin \left(\frac{2 \pi(0.48)}{0.1}\right)=-16.168=-16 A(2 \text { s.f })
$
Exam Tip
Remember to check that your calculator is in radians mode when using any of these equations. This is because angular frequency $\omega$ is measured in rad $\mathrm{s}^{-1}$
ROOT-MEAN-SQUARE CURRENT & VOLTAGE
Root-Mean-Square Current & Voltage
- Root-mean-square (r.m.s) values of current, or voltage, are a useful way of comparing a.c current, or voltage, to its equivalent direct current, or voltage
- The r.m.s values represent the d.c current, or voltage, values that will produce the same heating effect, or power dissipation, as the alternating current, or voltage
- The r.m.s value of an alternating current is defined as:
The value of a constant current that produces the same power in a resistor as the alternating current - The r.m.s current $\mathrm{t}_{\mathrm{r} . \mathrm{m} . \mathrm{s}}$ is defined by the equation:
$
\mathrm{I}_{\mathrm{r} . \mathrm{m} . \mathrm{s}}=\frac{I_0}{\sqrt{2}}
$
- So, r.m.s current is equal to $0.707 \times I_0$, which is about $70 \%$ of the peak current $I_0$
- The r.m.s value of an alternating voltage is defined as:
The value of a constant voltage that produces the same power in a resistor as the alternating voltage - The r.m.s voltage $V_{\text {r.m. }}$ is defined by the equation:
$
\mathrm{V}_{\mathrm{r} . \mathrm{m} . \mathrm{s}}=\frac{V_0}{\sqrt{2}}
$
- Where:
$
\begin{aligned}
& \text { – } I_0=\text { peak current }(\mathrm{A}) \\
& \text { – } \mathrm{V}_0=\text { peak voltage }(\mathrm{V})
\end{aligned}
$
- The r.m.s value is therefore defined as:
The steady direct current, or voltage, that delivers the same average power in a resistor as the alternating current, or voltage - A resistive load is any electrical component with resistance eg. a lamp
Worked example: Determining the r.m.s. current
An alternating current is l is represented by the equation
$
I=410 \sin (100 \pi t)
$
where l is measured in amperes and $t$ is in seconds. For this alternating current, determine the r.m.s current.
Step 1:
Write out the equation for r.m.s current
$
I_{\mathrm{r} . \mathrm{m} . \mathrm{s}}=\frac{I_0}{\sqrt{2}}
$
Step 2:
Determine the peak voltage $I_0$
- The alternating current equation is in the form: $\mathbf{I}=I_0 \sin (\omega t)$
- Comparing this to $I=410 \sin (100 \pi t)$ means the peak current is $I_0=$ 410 A
Step 3:
Substitute into the $I_{\mathrm{r} . \mathrm{m} . \mathrm{s}}$ equation
$
\mathrm{I}_{\mathrm{r} . \mathrm{m} . \mathrm{s}}=\frac{410}{\sqrt{2}}=289.91=290 \mathrm{~A}(2 \text { s.f. })
$
MEAN POWER
Mean Power
- In mains electricity, current and voltage are varying all the time
- This also means the power varies constantly, recall the equations for power:
$
\mathrm{P}=\mathrm{IV}=\mathrm{I}^2 \mathrm{R}=\frac{V^2}{R}
$
- Where:
- $\mathrm{I}=$ direct current $(A)$
- $V=$ direct voltage $(A)$
- $\mathrm{R}=$ resistance $(\Omega)$
- The r.m.s values means equations used for direct current and voltage can now be applied to alternating current and voltage
- They are also used determining an average current or voltage for alternating supplies
- Recall the equation for peak current:
$
\mathrm{I}_0=\sqrt{2} \mathrm{I}_{\mathrm{r} . \mathrm{m} . \mathrm{s}}
$
- Therefore, the peak (maximum) power is related to the mean (average) power by:
$
\mathrm{P}_{\text {mean }}=I_{\mathrm{r} . \mathrm{m} . \mathrm{s}} \mathrm{R}
$
$
P=I_0^2 R=\left(\sqrt{2} I_{r . m . s}\right)^2 R=2 I_{r . m . s} R=2 P_{\text {mean }}
$
$
\mathrm{P}_{\text {mean }}=\frac{P}{2}
$
- Therefore, it can be concluded that:
The mean power in a resistive load is half the maximum power for a sinusoidal alternating current or voltage
Worked example: Calculating mean power
An alternating voltage supplied across a resistor of $40 \Omega$ has a peak voltage $V_0$ of $240 \mathrm{~V}$. Calculate the mean power of this supply.
Step 1:
Write down the known quantities
Resistance, $R=40 \Omega$
Peak voltage, $V_0=240 \mathrm{~V}$
Step 2: Write out the equation for the peak power and calculate
Peak power, $\mathrm{P}=\frac{V_0^2}{R}$
$
P=\frac{(240)^2}{40}=1440 \mathrm{~W}
$
Step 3: $\quad$ Calculate the mean power
- The mean power is half of the maximum (peak) power
$
\text { Mean power }=1440 / 2=720 \mathrm{~W}
$
