CIE AS/A Level Physics 24.1 Production and use of ultrasound Study Notes- 2025-2027 Syllabus
CIE AS/A Level Physics 24.1 Production and use of ultrasound Study Notes – New Syllabus
CIE AS/A Level Physics 24.1 Production and use of ultrasound Study Notes at IITian Academy focus on specific topic and type of questions asked in actual exam. Study Notes focus on AS/A Level Physics latest syllabus with Candidates should be able to:
- understand that a piezo-electric crystal changes shape when a p.d. is applied across it and that the crystal generates an e.m.f. when its shape changes
- understand how ultrasound waves are generated and detected by a piezoelectric transducer
- understand how the reflection of pulses of ultrasound at boundaries between tissues can be used to obtain diagnostic information about internal structures
- define the specific acoustic impedance of a medium as \( Z = \rho c \), where ( c ) is the speed of sound in the medium
- use \( I_R / I_0 = (Z_1 – Z_2)^2 / (Z_1 + Z_2)^2 \) for the intensity reflection coefficient of a boundary between two media
- recall and use \( I = I_0 e^{-\mu x} \) for the attenuation of ultrasound in matter
Piezo-electric Effect: Change of Shape and Generation of e.m.f.
A piezo-electric crystal (such as quartz) has a remarkable property: it can convert electrical energy into mechanical deformation and mechanical deformation into electrical energy.
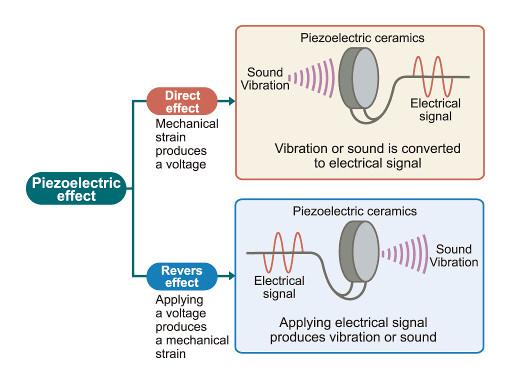
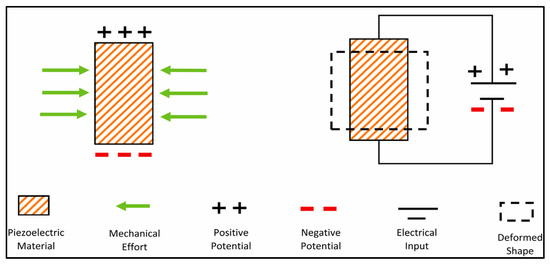
1. Applying a Potential Difference → Crystal Changes Shape
When a potential difference (p.d.) is applied across a piezo-electric crystal, the crystal distorts either compressing, stretching, or twisting.
- The electric field inside the crystal shifts the positions of positive and negative ions.
- This causes a change in the dimensions of the crystal.
- By applying an alternating p.d., the crystal vibrates at the same frequency.
This effect allows piezo-crystals to act as oscillators in devices such as quartz watches and ultrasound transmitters.
2. Changing the Shape of the Crystal → Generates an e.m.f.
If a mechanical force (compression, tension, bending) is applied to the crystal, it produces an electric charge separation across the crystal.
- This creates a potential difference (e.m.f.).
- The greater the deformation, the larger the induced e.m.f.
- This is used in microphones, pickups, and pressure sensors.
This is the reverse piezo-electric effect.
Summary
| Action | Effect on Crystal | Result |
|---|---|---|
| Apply p.d. across crystal | Crystal changes shape | Electrical → Mechanical |
| Deform the crystal | Crystal produces an e.m.f. | Mechanical → Electrical |
Example
A quartz crystal expands and contracts when an alternating voltage is applied. What property of the crystal allows this to happen?
▶️ Answer / Explanation
The piezo-electric effect: an applied voltage causes the crystal to change shape.
Example
In an electric guitar pickup, a piezo-electric strip generates a voltage when the strings vibrate. Explain why.
▶️ Answer / Explanation
The vibrating string compresses and bends the piezo-electric strip. This deformation causes charge separation in the crystal, producing an e.m.f.
Example
An ultrasound transducer uses a piezo-electric crystal driven at 2 MHz. Explain how the crystal produces the ultrasound waves.
▶️ Answer / Explanation
An alternating p.d. at 2 MHz is applied across the crystal. This causes the crystal to alternately expand and contract at the same frequency → mechanical vibrations at 2 MHz.
These high-frequency vibrations compress and rarefy the surrounding medium, generating ultrasound waves.
Generation and Detection of Ultrasound Waves Using a Piezoelectric Transducer
A piezoelectric transducer is a device that can both produce and detect ultrasound waves using the piezoelectric effect. It relies on the ability of a piezoelectric crystal to convert electrical energy into mechanical vibrations and vice versa.
1. Generation of Ultrasound Waves
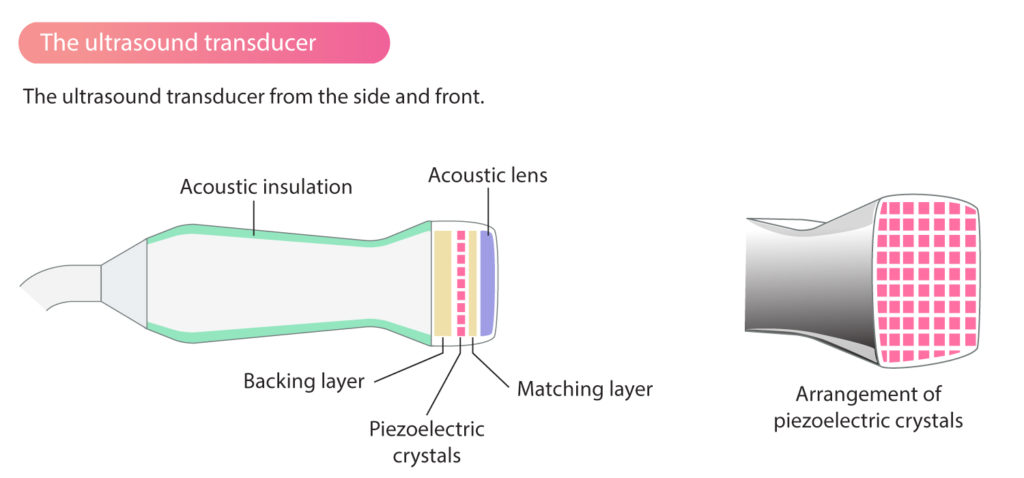
When an alternating potential difference (a.c.) is applied across a piezoelectric crystal, the crystal repeatedly expands and contracts.
This occurs because the electric field causes the ions in the crystal lattice to shift position, producing mechanical deformation.
- The frequency of the expansion–contraction matches the frequency of the applied a.c.
- If the a.c. frequency is in the ultrasound range (typically 1–15 MHz), the crystal vibrates at ultrasound frequency.
Thus, the transducer acts as an ultrasound transmitter.
2. Detection of Ultrasound Waves
When incoming ultrasound waves strike the crystal, they exert alternating pressure on it, causing it to deform (compress and expand).
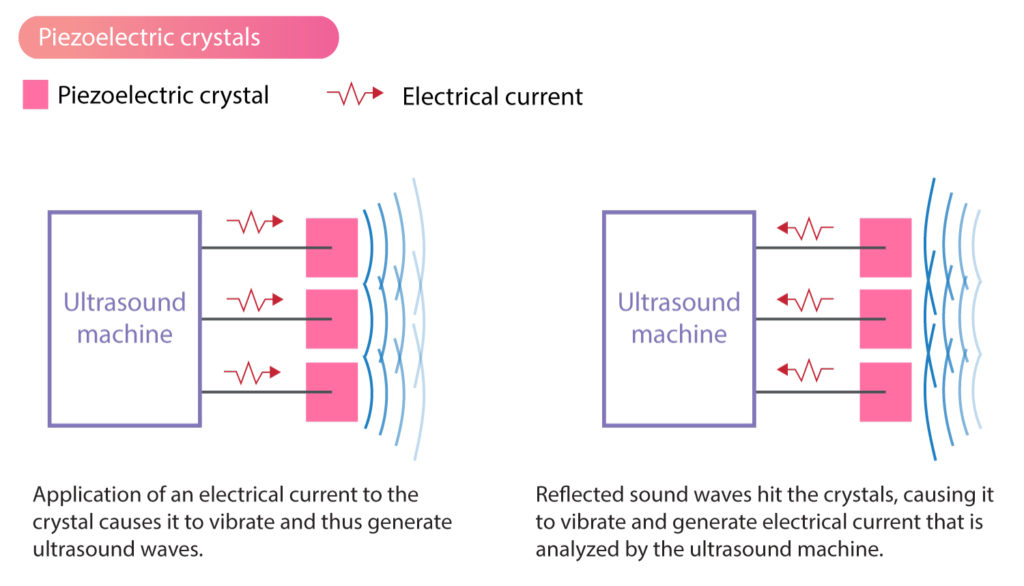
This deformation causes the ions inside the crystal to shift slightly, producing a voltage (e.m.f.) across its faces.
- This generated e.m.f. varies with the incoming ultrasound wave.
- The amplitude and timing of the signal provide information about the wave.
- The transducer therefore converts mechanical energy back into electrical energy.
Thus, the transducer acts as an ultrasound receiver.
3. Why the Same Device Can Transmit and Receive Ultrasound
Because the piezoelectric effect is reversible:
- Electrical → mechanical (expansion/contraction → ultrasound production)
- Mechanical → electrical (pressure/deformation → induced e.m.f.)
This makes piezoelectric crystals ideal for medical imaging and industrial ultrasound systems.
Example
Why does a piezoelectric crystal vibrate when an alternating potential difference is applied across it?
▶️ Answer / Explanation
The alternating p.d. causes the crystal to alternately expand and contract due to the piezoelectric effect, resulting in vibrations.
Example
Describe how a piezoelectric ultrasound transducer detects reflected ultrasound waves from tissue inside the body.
▶️ Answer / Explanation
Reflected ultrasound waves exert pressure on the crystal, making it deform slightly. This deformation produces a changing e.m.f., which is detected as an electrical signal corresponding to the incoming wave.
Example
An ultrasound transducer operates at 4 MHz. Explain how the transducer generates ultrasound of this frequency and how the same device can detect returning echoes.
▶️ Answer / Explanation
Generation:
- An a.c. voltage of frequency 4 MHz is applied across the piezoelectric crystal.
- The crystal expands and contracts at 4 MHz.
- This vibration produces compression and rarefaction waves in the medium → ultrasound at 4 MHz.
Detection:
- Reflected ultrasound waves strike the crystal, causing it to deform mechanically.
- The deformation induces an alternating e.m.f. across the crystal.
- This electrical signal corresponds to the returning echo.
Thus, because the piezoelectric effect is reversible, the same transducer works as both transmitter and receiver.
Using Reflected Ultrasound Pulses for Medical Diagnosis
Ultrasound imaging (sonography) relies on the fact that ultrasound pulses reflect from boundaries between different tissues in the body. These reflections (echoes) provide information that is used to build up an image of internal structures.
1. Reflection of Ultrasound at Tissue Boundaries
When an ultrasound pulse travels through the body, part of the wave is reflected at any boundary where the tissues have different acoustic impedances.
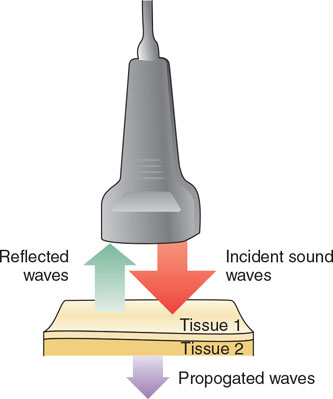
Acoustic impedance depends on:
- tissue density
- speed of sound in the tissue
Examples of boundaries:
- muscle → fat
- fluid → soft tissue
- soft tissue → bone
At these boundaries:
- Some ultrasound is reflected (echo)
- Some ultrasound continues deeper into the body
2. Detection of the Reflected Pulses
The returning echoes strike the piezoelectric transducer, causing it to generate an alternating e.m.f.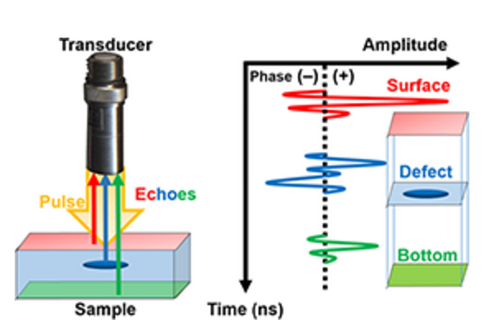
This electrical signal gives information about:
- How strong the reflection was (brightness)
- When the reflection was received (depth)
3. Determining Depth of Structures
The time between sending a pulse and receiving the reflected echo gives the distance to the boundary:
\( \mathrm{depth = \tfrac{1}{2} (speed\ in\ tissue) \times (time\ delay)} \)
The factor \( \tfrac{1}{2} \) accounts for the pulse travelling to the boundary and back.
4. Producing a Diagnostic Image
By sending repeated pulses and measuring echoes from many directions:
- Strong reflections → bright spots on screen
- Weak reflections → darker regions
- No reflections (e.g., fluid) → dark areas
This allows doctors to “see” inside the body without surgery.
Common Uses:
- Foetal imaging
- Heart imaging (echocardiography)
- Detecting cysts, tumours, and organ abnormalities
Example
A strong ultrasound echo is detected from a tissue boundary. What does this indicate about the two tissues?
▶️ Answer / Explanation
The tissues have very different acoustic impedances, causing a large portion of the ultrasound pulse to be reflected.
Example
An ultrasound pulse takes \( \mathrm{120\ \mu s} \) to return after reflecting from a boundary. If the speed of ultrasound in tissue is \( \mathrm{1600\ m/s} \), calculate the depth of the boundary.
▶️ Answer / Explanation
Use:
\( \mathrm{depth = \tfrac{1}{2} \, v t} \)
\( \mathrm{depth = \tfrac{1}{2}(1600)(120\times10^{-6})} \)
\( \mathrm{depth = 0.096\ m = 9.6\ cm} \)
Boundary is 9.6 cm deep.
Example
Explain why fluid-filled regions (e.g., the bladder) appear very dark on an ultrasound scan, while bone appears very bright.
▶️ Answer / Explanation
Fluids:
- Acoustic impedance changes very little at fluid–soft tissue boundaries.
- Very little reflection occurs → weak/no echoes.
- These areas appear dark.
Bones:
- Large impedance difference at soft tissue–bone boundary.
- Strong reflection → very strong echoes.
- Appears bright.
Specific Acoustic Impedance \( \mathrm{Z} \)
The specific acoustic impedance of a medium describes how much resistance the medium provides to the passage of a sound wave.
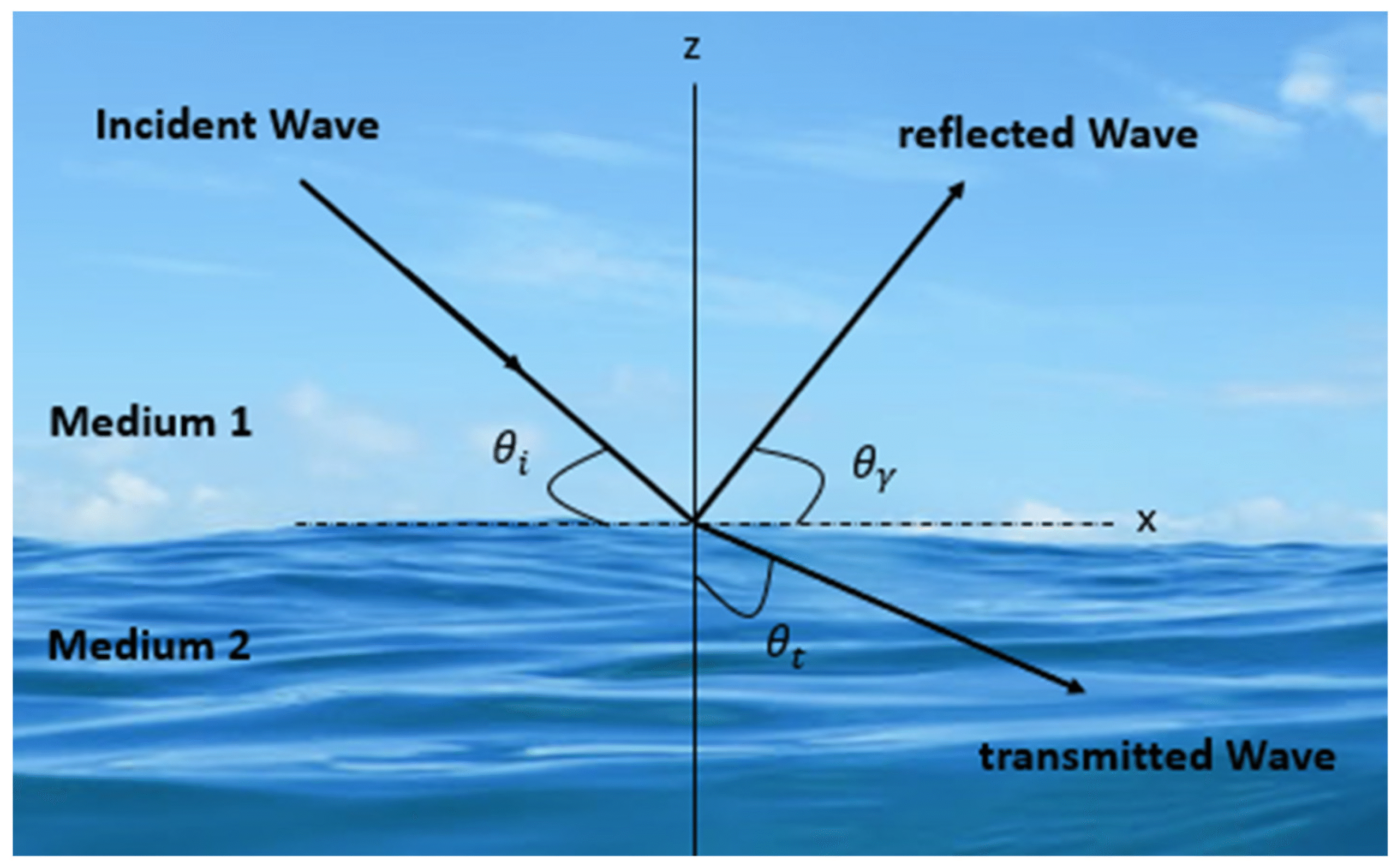
Definition:
The specific acoustic impedance of a medium is defined as \( \mathrm{Z = \rho c} \)
- \( \mathrm{Z} \) = acoustic impedance ( \( \mathrm{kg\,m^{-2}\,s^{-1}} \) )
- \( \mathrm{\rho} \) = density of the medium ( \( \mathrm{kg\,m^{-3}} \) )
- \( \mathrm{c} \) = speed of sound in the medium ( \( \mathrm{m/s} \) )
Meaning:
- High impedance → sound finds it harder to pass (e.g., bone)
- Low impedance → sound travels more easily (e.g., air)
- Reflection at boundaries occurs when two media have different impedances
This concept is crucial in ultrasound imaging because the difference in impedance determines how much ultrasound is reflected at tissue boundaries.
Example
The density of a soft tissue is \( \mathrm{1000\ kg/m^3} \), and the speed of sound in it is \( \mathrm{1500\ m/s} \). Calculate its acoustic impedance.
▶️ Answer / Explanation
\( \mathrm{Z = \rho c = (1000)(1500)} \)
\( \mathrm{Z = 1.5\times10^{6}\ kg\,m^{-2}\,s^{-1}} \)
Impedance = \( \mathrm{1.5\times10^{6}\ kg\,m^{-2}\,s^{-1}} \)
Example
Air has density \( \mathrm{1.2\ kg/m^3} \) and speed of sound \( \mathrm{340\ m/s} \). Calculate its acoustic impedance and compare it to that of soft tissue.
▶️ Answer / Explanation
Air:
\( \mathrm{Z = (1.2)(340) = 408\ kg\,m^{-2}\,s^{-1}} \)
This is much lower than soft tissue (\( \mathrm{1.5\times10^{6}} \)).
Interpretation: Very large impedance mismatch causes almost total reflection → this is why gel is needed in ultrasound scans.
Example
A certain boundary reflects 35% of the incident ultrasound intensity. Explain how the impedance difference between two tissues could lead to this level of reflection.
▶️ Answer / Explanation
The reflection coefficient depends on the impedance mismatch:
\( \mathrm{R = \left( \dfrac{Z_2 – Z_1}{Z_2 + Z_1} \right)^2 } \)
If \( \mathrm{Z_1} \) and \( \mathrm{Z_2} \) differ significantly (but not extremely, as with bone), a substantial percentage such as 35% can be reflected.
This means the tissues on either side have noticeably different values of \( \mathrm{\rho c} \).
Intensity Reflection Coefficient at a Boundary
When an ultrasound wave meets a boundary between two media with different acoustic impedances, part of the wave is reflected and part is transmitted.
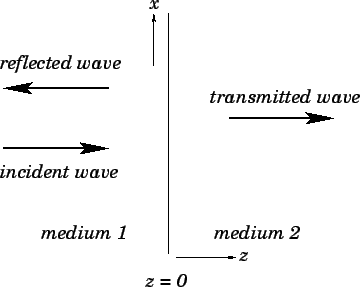
The fraction of the incident intensity that is reflected is given by the intensity reflection coefficient:
\( \mathrm{\dfrac{I_R}{I_0} = \left( \dfrac{Z_1 – Z_2}{Z_1 + Z_2} \right)^2 } \)
- \( \mathrm{I_R} \) = reflected intensity
- \( \mathrm{I_0} \) = incident intensity
- \( \mathrm{Z_1} \) = acoustic impedance of medium 1
- \( \mathrm{Z_2} \) = acoustic impedance of medium 2
Interpretation:
- If \( \mathrm{Z_1 = Z_2} \): no reflection (perfect transmission).
- If impedances are very different (large mismatch): strong reflection.
- A huge mismatch (e.g., air–tissue) gives almost total reflection.
Example
Two tissues have acoustic impedances \( \mathrm{Z_1 = 1.5\times10^6} \) and \( \mathrm{Z_2 = 1.6\times10^6\ kg\,m^{-2}\,s^{-1}} \). Calculate the reflection coefficient.
▶️ Answer / Explanation
Use:
\( \mathrm{R = \left( \dfrac{Z_1 – Z_2}{Z_1 + Z_2} \right)^2} \)
\( \mathrm{R = \left( \dfrac{1.5 – 1.6}{1.5 + 1.6} \right)^2 } \)
\( \mathrm{R = \left( \dfrac{-0.1}{3.1} \right)^2 = ( -0.03226 )^2 } \)
\( \mathrm{R = 0.00104} \)
Only 0.10% is reflected — a weak reflection.
Example
Soft tissue has \( \mathrm{Z_1 = 1.6\times10^6} \). Bone has \( \mathrm{Z_2 = 7.8\times10^6} \). Find the fraction of intensity reflected at the boundary.
▶️ Answer / Explanation
\( \mathrm{R = \left( \dfrac{1.6 – 7.8}{1.6 + 7.8} \right)^2 } \)
\( \mathrm{R = \left( \dfrac{-6.2}{9.4} \right)^2 = ( -0.6596 )^2 } \)
\( \mathrm{R = 0.435 } \)
About 43.5% of the intensity is reflected — a strong echo.
Example
Air has acoustic impedance \( \mathrm{Z_1 = 400} \). Soft tissue has impedance \( \mathrm{Z_2 = 1.5\times10^6} \). Calculate the reflection coefficient and explain why ultrasound gel is required in imaging.
▶️ Answer / Explanation
Step 1: Calculate reflection coefficient
\( \mathrm{R = \left( \dfrac{400 – 1.5\times10^6}{400 + 1.5\times10^6} \right)^2 } \)
The denominator ≈ \( \mathrm{1.5004\times10^6} \). The numerator ≈ \( \mathrm{-1.4996\times10^6} \).
\( \mathrm{R \approx \left( \dfrac{-1.4996\times10^6}{1.5004\times10^6} \right)^2 } \)
\( \mathrm{R \approx ( -0.9995 )^2 = 0.999 } \)
≈ 99.9% reflection!
Explanation:
- The impedance mismatch between air and tissue is enormous.
- Almost all ultrasound is reflected at the skin surface.
- Ultrasound gel removes the air gap → matching layer → improves transmission.
This is why gel is essential for ultrasound scans.
Attenuation of Ultrasound in Matter: \( \mathrm{I = I_0 e^{-\mu x}} \)
As ultrasound travels through a material, its intensity decreases due to:
- absorption (conversion into heat)
- scattering
- reflection at small internal boundaries
This loss of intensity is called attenuation.
Attenuation Formula
\( \mathrm{I = I_0 e^{-\mu x}} \)
- \( \mathrm{I} \) = intensity after travelling distance \( \mathrm{x} \)
- \( \mathrm{I_0} \) = initial intensity
- \( \mathrm{\mu} \) = attenuation coefficient (m\(^{-1}\))
- \( \mathrm{x} \) = distance travelled in the medium
Meaning:
- Larger \( \mathrm{\mu} \) → faster attenuation (stronger weakening of ultrasound)
- Small \( \mathrm{\mu} \) → ultrasound travels deeper with less loss
- The process is exponential, similar to radioactive decay
Example
An ultrasound beam enters tissue with initial intensity \( \mathrm{I_0 = 100\ W/m^2} \). If the attenuation coefficient is \( \mathrm{\mu = 0.20\ cm^{-1}} \), find the intensity after travelling \( \mathrm{5\ cm} \).
▶️ Answer / Explanation
Use the formula:
\( \mathrm{I = I_0 e^{-\mu x}} \)
\( \mathrm{I = 100\, e^{-0.20 \times 5}} \)
\( \mathrm{I = 100\, e^{-1}} = 100 \times 0.3679 \)
\( \mathrm{I \approx 36.8\ W/m^2} \)
Intensity after 5 cm = \( \mathrm{36.8\ W/m^2} \)
Example
An ultrasound wave has initial intensity \( \mathrm{80\ W/m^2} \). After travelling \( \mathrm{10\ cm} \) in tissue, its intensity is \( \mathrm{20\ W/m^2} \). Calculate the attenuation coefficient \( \mathrm{\mu} \).
▶️ Answer / Explanation
Use:
\( \mathrm{I = I_0 e^{-\mu x}} \Rightarrow \dfrac{I}{I_0} = e^{-\mu x} \)
\( \mathrm{\dfrac{20}{80} = e^{-10\mu}} \)
\( \mathrm{0.25 = e^{-10\mu}} \)
Take natural log:
\( \mathrm{\ln(0.25) = -10\mu} \)
\( \mathrm{-1.386 = -10\mu} \)
\( \mathrm{\mu = 0.1386\ cm^{-1}} \)
Attenuation coefficient = \( \mathrm{0.139\ cm^{-1}} \)
Example
Ultrasound is used to image a deep structure \( \mathrm{20\ cm} \) inside the body. The attenuation coefficient is \( \mathrm{0.30\ cm^{-1}} \). What fraction of the original intensity reaches the structure?
▶️ Answer / Explanation
Since the question asks for a fraction:
\( \mathrm{\dfrac{I}{I_0} = e^{-\mu x}} \)
\( \mathrm{\dfrac{I}{I_0} = e^{-0.30 \times 20}} \)
\( \mathrm{\dfrac{I}{I_0} = e^{-6}} \)
\( \mathrm{\dfrac{I}{I_0} = 0.00248} \)
Only 0.25% of the original intensity reaches the structure.
This shows why ultrasound struggles to penetrate deep or dense tissues.
