THE PIEZOELECTRIC TRANSDUCER
- The piezoelectric effect is defined as:
The ability of particular materials to generate a potential difference (p.d.) by transferring mechanical energy to electrical energy
- A transducer is any device that converts energy from one form to another
Piezoelectric Crystals
- At the heart of a piezoelectric transducer is a piezoelectric crystal
- Piezoelectric crystals are materials which produce a p.d. when they are deformed
- This deformation can be by compression or stretching
- If a p.d. is applied to a piezoelectric crystal, then it deforms, and if the p.d. is reversed, then it expands
- If this is an alternating p.d. then the crystal will vibrate at the same frequency as the alternating voltage
- Crystals must be cut to a certain size in order to induce resonance
- One of the most common piezoelectric crystals is quartz, which is made from a lattice of silicon dioxide atoms
- When the lattice is distorted, the structure becomes charged creating an electric field and, as a result, an electric current
- If an electric current is applied to the crystal, then this causes the shape of the lattice to alternate which produces a sound wave
- Due to the conventional direction of electric current, it will flow from the positive to negative region of the crystal
Applications of the Piezoelectric Transducer
- Microphone
- A piezoelectric microphone detects pressure variations in sound waves
- These can then be converted to an electrical signal for processing
- Ultrasound
- In a piezoelectric transducer, an alternating p.d. is applied to produce ultrasound waves and sent into the patient’s body
- The returning ultrasound waves induce a p.d. in the transducer for analysis by a healthcare professional
GENERATING & USING ULTRASOUND
- An ultrasound is defined as:
A high frequency sound above the range of human hearing - This is above $20 \mathrm{kHz}$, although in medical applications the frequencies can be up to the $\mathrm{MHz}$ range
- An ultrasound transducer is made up of a piezoelectric crystal and electrodes which produce an alternating p.d.
- The crystal is heavily damped, usually with epoxy resin, to stop the crystal from vibrating too much
- This produces short pulses and increases the resolution of the ultrasound device
- A piezoelectric crystal can act as both a receiver or transmitter of ultrasound
- When it is receiving ultrasound, it converts the sound waves into an alternating p.d.
- When it is transmitting ultrasound, it converts an alternating p.d. into sound waves
Worked example
Explain the principles of the generation and detection of ultrasound waves.
Generation:
- An alternating p.d. is applied across a piezo-electric crystal, causing it to change shape
- The alternating p.d. causes the crystal to vibrate and produce ultrasound waves
- The crystal vibrates at the frequency of the alternating p.d., so, the crystal must be cut to a specific size in order to produce resonance
Detection:
- When the ultrasound wave returns, the crystal vibrates which produces an alternating p.d. across the crystal
- This received signal can then be processed and used for medical diagnosis
Using Ultrasound in Medical Imaging
- In an ultrasound scanner, the transducer sends out a beam of sound waves into the body
- The sound waves are reflected back to the transducer by boundaries between tissues in the path of the beam
- For example, the boundary between fluid and soft tissue or tissue and bone
- When these echoes hit the transducer, they generate electrical signals that are sent to the ultrasound scanner
- Using the speed of sound and the time of each echo’s return, the scanner calculates the distance from the transducer to the tissue boundary
- These distances can be used to generate two-dimensional images of tissues and organs
- The frequency of the ultrasound is important because:
- The higher the frequency of the ultrasound, the higher the resolution and the smaller structures that can be distinguished
- The ultrasound gives two main pieces of information about the boundary:
- Depth: the time between transmission and receipt of the pulse (the time delay)
- Nature: amount of transmitted intensity received (will vary depending on the type of tissue)
Worked example
Explain the main principles behind the use of ultrasound to obtain diagnostic information about internal body structures.
Answer/Explanation
- A pulse of ultrasound is emitted by the piezo-electric crystal
- This is reflected from the boundaries between media
- The reflected pulse is detected by the ultrasound transmitter
- The signal is then processed and displayed on the screen for the healthcare worker to analyse and use for medical diagnosis
- The intensity of the reflection gives information about the nature of the boundary
- The time between transmission and receipt of the pulse (the time delay) gives information about the depth of the boundary
Exam Tip
6 mark exam questions about this topic are very common, make sure you practice writing about using and detecting ultrasounds in full, coherent sentences with correct spelling and grammar. Writing short or vague answers could lose you marks, as well as misspelling words!
SPECIFIC ACOUSTIC IMPEDANCE
- The acoustic impedance, $Z$, of a medium is defined as:
The product of the speed of the ultrasound in the medium and the density of the medium - This quantity describes how much resistance an ultrasound beam encounters as it passes through a tissue
- Acoustic impedance can be calculated using the equation:
$
\mathbf{Z}=\rho c
$
- Where:
- $Z=$ acoustic impedance $\left(\mathrm{kg} \mathrm{m}^{-2} \mathrm{~s}^{-1}\right)$
- $\circ \rho=$ the density of the material $\left(\mathrm{kg} \mathrm{m}^{-3}\right)$
- $\circ \mathrm{c}=$ the speed of sound in the material $\left(\mathrm{m} \mathrm{s}^{-1}\right)$
- This equation tells us:
- The higher the density of a tissue, the greater the acoustic impedance
- The faster the ultrasound travels through the material, the greater the acoustic impedance also
- This is because sound travels faster in denser materials
- Sound is fastest in solids and slowest in gases
- The closer the particles in the material, the faster the vibrations can move through the material
- At the boundary between media of different acoustic impedances, some of the wave energy is reflected and some is transmitted
- The greater the difference in acoustic impedance between the two media, the greater the reflection and the smaller the transmission
- Two materials with the same acoustic impedance would give no reflection
- Two materials with a large difference in values would give much larger reflections
- Air has an acoustic impedance of $Z_{\mathrm{air}}=400 \mathrm{~kg} \mathrm{~m}^{-2} \mathrm{~s}^{-1}$
- Skin has an acoustic impedance of $Z_{5 k i n}=1.7 \times 10^6 \mathrm{~kg} \mathrm{~m}^{-2} \mathrm{~s}^{-1}$
- The large difference means ultrasound would be significantly reflected, hence a coupling gel is necessary
- The coupling gel used has a similar $Z$ value to skin, meaning that very little ultrasound is reflected
Worked example: Calculating bone density
The table shows the speed of sound acoustic impedance in four different materials. Use this to calculate the value for the density of bone.
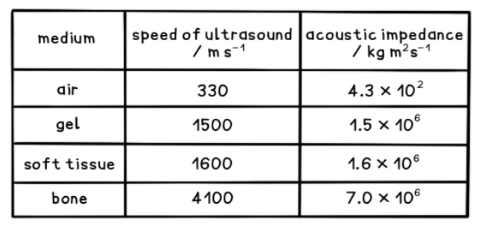
Answer/Explanation
Step 1:
$\quad$ Write down known quantities
Acoustic impedance of bone, $Z=7.0 \times 10^6 \mathrm{~kg} \mathrm{~m}^{-2} \mathrm{~s}^{-1}$
Speed of ultrasound in bone, $c=4100 \mathrm{~m} \mathrm{~s}^{-1}$
Step 2:
Write out the equation for acoustic impedance
$
\mathbf{Z}=\rho \mathbf{c}
$
Step 3:
Rearrange for density and calculate
$
\rho=\frac{Z}{c}=\frac{7.0 \times 10^6}{4100}=1700 \mathrm{~kg} \mathrm{~m}^{-3}
$
Exam Tip
A common mistake is to confuse the $\mathrm{c}$ in the acoustic impedance equation for the speed of light – don’t do this!
2INTENSITY REFLECTION COEFFICIENT
- The intensity reflection coefficient $\alpha$ is defined as:
The ratio of the intensity of the reflected wave relative to the incident (transmitted) wave - This can be calculated using the fraction:
$
\alpha=\frac{I_r}{I_0}=\frac{\left(Z_2-Z_1\right)^2}{\left(Z_2+Z_1\right)^2}
$
- Where:
- $\alpha=$ intensity reflection coefficient
- $I_R=$ intensity of the reflected wave $\left(\mathrm{W} \mathrm{m}^{-2}\right)$
- $1_0=$ intensity of the incident wave $\left(\mathrm{W}^{-2}\right)$
- $Z_1=$ acoustic impedance of one material $\left(\mathrm{kg} \mathrm{m}^{-2} \mathrm{~s}^{-1}\right)$
- $Z_2=$ acoustic impedance of a second material $\left(\mathrm{kg} \mathrm{m}^{-2} \mathrm{~s}^{-1}\right)$
- This equation will be provided on the datasheet for your exam
- This ratio shows:
- If there is a large difference between the impedance of the two materials, then most of the energy will be reflected
- If the impedance is the same, then there will be no reflection
Coupling Medium
- When ultrasound is used in medical imaging, a coupler is needed between the transducer and the body
- The soft tissues of the body are much denser than air
- If air is present between the transducer and the body, then almost all the ultrasound energy will be reflected
- The coupling gel is placed between the transducer and the body, as skin and the coupling gel have a similar density, so little ultrasound is reflected
- This is an example of impedance matching
Worked example: Intensity reflection coefficient
A beam of ultrasound is incident at right-angles to a boundary between two materials as shown in the diagram.
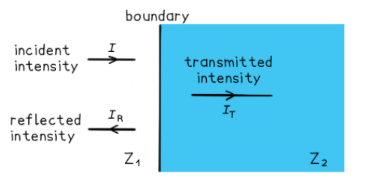
The materials have acoustic impedances of $Z_1$ and $Z_2$. The intensity of the transmitted ultrasound beam is $\mathrm{I}_{\mathrm{T}}$, and the reflected intensity is $\mathrm{I}_{\mathrm{R}}$.

a) What is the relationship between $\mathrm{I}, \mathrm{I}_{\mathrm{T}}$ and $\mathrm{I}_{\mathrm{R}}$ ?
b) Use the data from the table to determine the reflection coefficient $\alpha$ for a boundary between
i) gel and soft tissue.
ii) air and soft tissue.
c) Explain why gel is usually put on the skin during medical diagnosis using ultrasound.
Part (a)
Incident intensity = Transmitted intensity + Reflected intensity
$
\mathbf{I}=\mathbf{I}_{\mathrm{T}}+\mathbf{I}_{\mathrm{R}}
$
Part (b)(i)
Step 1:
Write down the equation for intensity reflection coefficient $\alpha$
$
\alpha=\frac{\left(Z_2-Z_1\right)^2}{\left(Z_2+Z_1\right)^2}
$
Step 2:
Write down the acoustic impedances for gel and soft tissue
Gel, $Z_1=1.5 \times 10^6 \mathrm{~kg} \mathrm{~m}^{-2} \mathrm{~s}^{-1}$
Soft tissue, $Z_2=1.6 \times 10^6 \mathrm{~kg} \mathrm{~m}^{-2} \mathrm{~s}^{-1}$
Step 3:
Calculate the intensity reflection coefficient
$
\alpha=\frac{\left(1.6 \times 10^6-1.5 \times 10^6\right)^2}{\left(1.6 \times 10^6+1.5 \times 10^6\right)^2}=\frac{(0.1)^2}{(3.1)^2}=0.001
$
This result means that only $\mathbf{0 . 1 \%}$ of the incident intensity will be reflected, with the remaining being transmitted
Part (b)(ii)
Step 1:
Write down the acoustic impedances for air and soft tissue
Air, $Z_1=4.3 \times 10^2 \mathrm{~kg} \mathrm{~m}^{-2} \mathrm{~s}^{-1}$
Soft tissue, $Z_2=1.6 \times 10^6 \mathrm{~kg} \mathrm{~m}^{-2} \mathrm{~s}^{-1}$
Step 2:
Calculate the intensity reflection coefficient
$
\alpha=\frac{\left(1.6 \times 10^6-4.3 \times 10^2\right)^2}{\left(1.6 \times 10^6+4.3 \times 10^2\right)^2} \approx \frac{\left(1.6 \times 10^6\right)^2}{\left(1.6 \times 10^6\right)^2} \approx 1
$
This result means that $\mathbf{1 0 0} \%$ of the incident intensity will be reflected, with none being transmitted
Part (c)
- At the air-soft tissue boundary, the intensity reflection coefficient is $\alpha \approx 1$
- Therefore, without gel, there is almost complete reflection – no ultrasound is transmitted through the skin
- At the gel-soft tissue boundary, the intensity reflection coefficient is $\alpha=0.001$
- Therefore, the gel enables almost complete transmission of the ultrasound through the skin, with very little reflection
ATTENUATION OF ULTRASOUND IN MATTER
- Attenuation of ultrasound is defined as:
The reduction of energy due to the absorption of ultrasound as it travels through a material - The attenuation coefficient of the ultrasound is expressed in decibels per centimetre lost for every incremental increase in megahertz frequency
- Generally, $0.5 \mathrm{~dB} / \mathrm{cm}$ is lost for every $1 \mathrm{MHz}$
- The intensity I of the ultrasound decreases with distance $x$, according to the equation:
$
I=10 e^{-\mu x}
$
- Where:
- $10=$ the intensity of the incident beam $\left(\mathrm{W} \mathrm{m} \mathrm{m}^{-2}\right)$
- $\circ I=$ the intensity of the reflected beam $\left(\mathrm{W} \mathrm{m} \mathrm{m}^{-2}\right)$
- $\mu=$ the absorption coefficient $\left(\mathrm{m}^{-1}\right)$
- $x=$ distance travelled through the material $(\mathrm{m})$
- The absorption coefficient $\mu$, will vary from material to material
- Attenuation is not a major problem in ultrasound scanning as the scan relies on the reflection of the ultrasounds at boundaries of materials
Worked example: Attenuation of ultrasound
The thickness $x$ of the layer of fat on an animal, as shown in the diagram, is to be investigated using ultrasound.
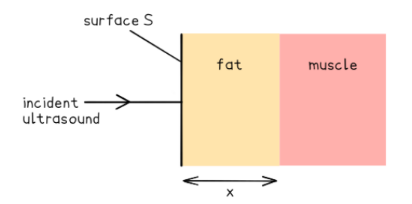
The intensity of the parallel ultrasound beam entering the surface $S$ of the layer of fat is I. The beam is reflected from the boundary between fat and muscle. The intensity of the reflected ultrasound detected at the surface $S$ of the fat is 0.012I.

Using the table calculate:
a) The intensity reflection coefficient at the boundary between the fat and the muscle.
b) The thickness $x$ of the layer of fat.
Answer/Explanation
Part (a)
Step 1:
Write down the equation for intensity reflection coefficient $\alpha$
$
\alpha=\frac{\left(Z_2-Z_1\right)^2}{\left(Z_2+Z_1\right)^2}
$
Step 2:
Calculate the intensity reflection coefficient
$
\alpha=\frac{\left(1.7 \times 10^6-1.3 \times 10^6\right)^2}{\left(1.7 \times 10^6+1.3 \times 10^6\right)^2}=\frac{(0.4)^2}{(3)^2}=0.018
$
This means that $\mathbf{0 . 0 1 8}$ of the intensity is reflected at the interface between fat and muscle. This reflected intensity will move back through the fat towards surface $S$.
Part (b)
Step 1:
Write out the known quantities
The intensity of the ultrasound pulse is affected 3 times:
1. Attenuation from the surface $S$ to the fat-muscle boundary
2. Reflection at the boundary
3. Attenuation from the boundary back to the surface $\mathrm{S}$
After being transmitted in the fat, the intensity at surface $S$ is given to be $0.012 \mathrm{I}$.
Therefore, the intensity is $0.018 \mathrm{I}$ at the fat-muscle boundary, and as the ultrasound moves through the fat, it gets attenuated and the new intensity at the surface $\mathrm{S}$ is now $0.012 \mathrm{I}$
Incident intensity, equal to the intensity of the reflected pulse, $10=0.0181 \times \mathrm{e}^{-\mu x}$
Transmitted intensity, $I=0.012 I$
Absorption coefficient, $\mu=48 \mathrm{~m}^{-1}$
Thickness of fat $=x$
Step 2:
Write out the equation for attenuation
$
I=I_0 e^{-\mu x}
$
Step 3:
Substitute in values for intensity and simplify
$
\begin{gathered}
0.012 I=\left[0.018 I \times e^{-\mu x}\right] \times e^{-\mu x} \\
0.012=0.018 \mathrm{e}^{-2 \mu x}
\end{gathered}
$
Step 4:
Rearrange and take the natural log of both sides
$
\begin{gathered}
\frac{0.012}{0.018}=e^{-2 \mu x} \\
\ln \left(\frac{0.012}{0.018}\right)=-2 \mu x
\end{gathered}
$
Step 5:
Rearrange and calculate the thickness $\mathrm{x}$
$
x=\frac{\ln \left(\frac{0.012}{0.018}\right)}{-2 \mu}=\frac{\ln \left(\frac{0.012}{0.018}\right)}{-2 \times 48}=4.22 \times 10^{-3} \mathrm{~m}=\mathbf{0 . 4 2} \mathbf{c m}
$
Exam Tip
The intensity equation will not be provided for you on your exam datasheet, so make sure you remember this!
