CIE AS/A Level Physics 25.2 Stellar radii Study Notes- 2025-2027 Syllabus
CIE AS/A Level Physics 25.2 Stellar radii Study Notes – New Syllabus
CIE AS/A Level Physics 25.2 Stellar radii Study Notes at IITian Academy focus on specific topic and type of questions asked in actual exam. Study Notes focus on AS/A Level Physics latest syllabus with Candidates should be able to:
- recall and use Wien’s displacement law \( \lambda_{\text{max}} \propto 1/T \) to estimate the peak surface temperature of a star
- use the Stefan–Boltzmann law \( L = 4\pi \sigma r^2 T^4 \)
- use Wien’s displacement law and the Stefan–Boltzmann law to estimate the radius of a star
Wien’s Displacement Law and Estimating the Peak Surface Temperature of a Star
Wien’s displacement law relates the temperature of a star’s surface to the wavelength at which it emits the maximum intensity of radiation.
Wien’s Displacement Law 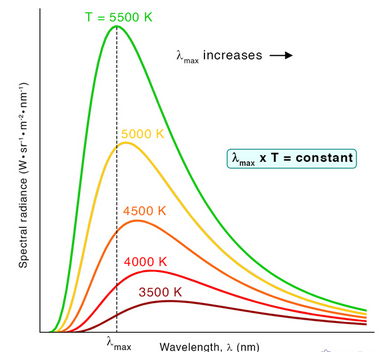
\( \mathrm{\lambda_{\text{max}} T = b} \)
- \( \mathrm{\lambda_{\text{max}}} \) = wavelength of maximum emission (m)
- \( \mathrm{T} \) = surface temperature (K)
- \( \mathrm{b} \) = Wien’s constant \( \mathrm{b = 2.90\times10^{-3}\ m\,K} \)
This shows:
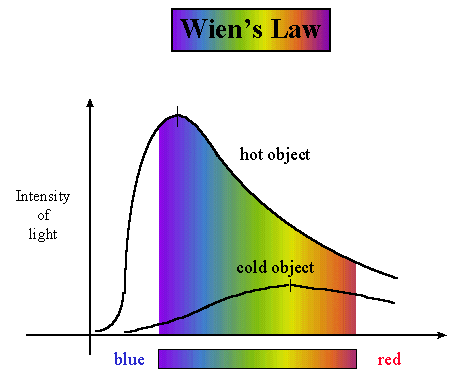
Hotter stars → shorter peak wavelength (bluer)
Cooler stars → longer peak wavelength (redder)
Estimating Star Temperature
Rearranging:
\( \mathrm{T = \dfrac{b}{\lambda_{\text{max}}}} \)
If we know a star’s peak emission wavelength, we can estimate its surface temperature.
Example
The peak wavelength of a star’s emission is \( \mathrm{580\ nm} \). Estimate the star’s surface temperature.
▶️ Answer / Explanation
Convert to metres:
\( \mathrm{580\ nm = 580\times10^{-9}\ m} \)
Use Wien’s law:
\( \mathrm{T = \dfrac{2.90\times10^{-3}}{580\times10^{-9}}} \)
\( \mathrm{T \approx 5000\ K} \)
The star’s temperature ≈ 5000 K.
Example
A blue star has a peak emission wavelength of \( \mathrm{300\ nm} \). Calculate its surface temperature.
▶️ Answer / Explanation
Convert wavelength:
\( \mathrm{300\ nm = 300\times10^{-9}\ m} \)
Apply Wien’s law:
\( \mathrm{T = \dfrac{2.90\times10^{-3}}{300\times10^{-9}}} \)
\( \mathrm{T \approx 9667\ K} \)
Temperature ≈ \( \mathrm{9.7\times10^3\ K} \)
Example
A star appears deep red, and its peak wavelength is measured as \( \mathrm{850\ nm} \). Estimate its surface temperature and comment on the star type.
▶️ Answer / Explanation
Convert wavelength:
\( \mathrm{850\ nm = 850\times10^{-9}\ m} \)
Calculate temperature:
\( \mathrm{T = \dfrac{2.90\times10^{-3}}{850\times10^{-9}}} \)
\( \mathrm{T \approx 3410\ K} \)
Temperature ≈ 3400 K.
This temperature corresponds to a cool red star, likely a red giant or an M-type main-sequence star.
Stefan–Boltzmann Law for Stellar Luminosity
The Stefan–Boltzmann law relates the luminosity of a star to its radius and surface temperature.
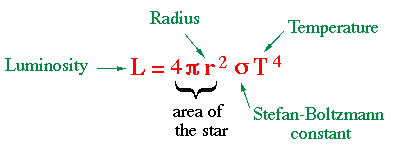
Stefan–Boltzmann Law
\( \mathrm{L = 4\pi \sigma r^2 T^4} \)
- \( \mathrm{L} \) = luminosity (W)
- \( \mathrm{r} \) = radius of the star (m)
- \( \mathrm{T} \) = surface temperature (K)
- \( \mathrm{\sigma} \) = Stefan–Boltzmann constant \( \mathrm{\sigma = 5.67\times10^{-8}\ W\,m^{-2}\,K^{-4}} \)
This law states that:
- A hotter star emits much more energy (because of the \( \mathrm{T^4} \) dependence).
- A larger star emits more energy (because of the \( \mathrm{r^2} \) term).
Rearranging if Needed
To find radius:
\( \mathrm{r = \sqrt{\dfrac{L}{4\pi \sigma T^4}}} \)
To find temperature:
\( \mathrm{T = \left( \dfrac{L}{4\pi \sigma r^2} \right)^{1/4}} \)
Example
A star has radius \( \mathrm{1.0\times10^9\ m} \) and temperature \( \mathrm{6000\ K} \). Calculate its luminosity.
▶️ Answer / Explanation
Use
\( \mathrm{L = 4\pi \sigma r^2 T^4} \)
Substitute values:
\( \mathrm{L = 4\pi (5.67\times10^{-8})(1.0\times10^9)^2 (6000)^4} \)
Compute step by step:
- \( \mathrm{r^2 = 1.0\times10^{18}} \)
- \( \mathrm{T^4 = 1.296\times10^{15}} \)
- Combine: \( \mathrm{L \approx 4\pi (5.67\times10^{-8})(1.0\times10^{18})(1.296\times10^{15})} \)
- \( \mathrm{L \approx 9.2\times10^{26}\ W} \)
Luminosity ≈ \( \mathrm{9.2\times10^{26}\ W} \)
Example
A star has luminosity \( \mathrm{3.0\times10^{28}\ W} \) and temperature \( \mathrm{8000\ K} \). Calculate its radius.
▶️ Answer / Explanation
Use:
\( \mathrm{r = \sqrt{\dfrac{L}{4\pi \sigma T^4}}} \)
Substitute:
\( \mathrm{r = \sqrt{\dfrac{3.0\times10^{28}}{4\pi (5.67\times10^{-8})(8000)^4}}} \)
Compute:
- \( \mathrm{T^4 = 4.096\times10^{15}} \)
- Denominator: \( \mathrm{4\pi (5.67\times10^{-8})(4.096\times10^{15}) \approx 2.92\times10^{9}} \)
- \( \mathrm{r = \sqrt{\dfrac{3.0\times10^{28}}{2.92\times10^{9}}}} \)
- \( \mathrm{r = \sqrt{1.03\times10^{19}} = 1.01\times10^{9}\ m} \)
Radius ≈ \( \mathrm{1.0\times10^9\ m} \)
Example
A red giant has radius \( \mathrm{5\times10^{10}\ m} \) and luminosity \( \mathrm{2\times10^{29}\ W} \). Estimate its surface temperature.
▶️ Answer / Explanation
Use:
\( \mathrm{T = \left( \dfrac{L}{4\pi \sigma r^2} \right)^{1/4}} \)
Calculate denominator:
- \( \mathrm{r^2 = (5\times10^{10})^2 = 2.5\times10^{21}} \)
- \( \mathrm{4\pi\sigma r^2 = 4\pi (5.67\times10^{-8})(2.5\times10^{21})} \)
- ≈ \( \mathrm{1.78\times10^{15}} \)
Now:
\( \mathrm{T = \left( \dfrac{2\times10^{29}}{1.78\times10^{15}} \right)^{1/4}} \)
\( \mathrm{T = \left(1.12\times10^{14}\right)^{1/4}} \)
\( \mathrm{T \approx 3500\ K} \)
Surface temperature ≈ 3500 K.
Using Wien’s Displacement Law and the Stefan–Boltzmann Law to Estimate the Radius of a Star
To estimate a star’s radius, we typically know two observable quantities:

- its peak wavelength of emission \( \mathrm{\lambda_{max}} \)
- its luminosity \( \mathrm{L} \)
From these, we use:
- Wien’s displacement law to find temperature \( \mathrm{T} \)
- Stefan–Boltzmann law to find radius \( \mathrm{r} \)
Step 1 — Use Wien’s Displacement Law
\( \mathrm{\lambda_{max} T = b} \)
- \( \mathrm{b = 2.90\times10^{-3}\ m\,K} \)
So:
\( \mathrm{T = \dfrac{b}{\lambda_{max}}} \)
Step 2 — Use Stefan–Boltzmann Law
\( \mathrm{L = 4\pi \sigma r^{2} T^{4}} \)
Rearrange to find radius:
\( \mathrm{r = \sqrt{\dfrac{L}{4\pi \sigma T^{4}}}} \)
Example
A star has a peak wavelength of \( \mathrm{600\ nm} \). Its luminosity is \( \mathrm{3.8\times10^{26}\ W} \). Estimate its radius.
▶️ Answer / Explanation
Step 1: Convert wavelength
\( \mathrm{600\ nm = 600\times10^{-9}\ m} \)
Step 2: Find temperature using Wien’s law
\( \mathrm{T = \dfrac{2.90\times10^{-3}}{600\times10^{-9}} = 4833\ K} \)
Step 3: Use Stefan–Boltzmann law to find radius
\( \mathrm{r = \sqrt{\dfrac{3.8\times10^{26}}{4\pi(5.67\times10^{-8})(4833)^4}}} \)
Compute \( \mathrm{T^4 = 5.47\times10^{14}} \)
\( \mathrm{r = \sqrt{\dfrac{3.8\times10^{26}}{3.91\times10^{8}}}} \)
\( \mathrm{r = \sqrt{9.72\times10^{17}} = 9.86\times10^{8}\ m} \)
Radius ≈ \( \mathrm{1.0\times10^{9}\ m} \)
Example
A blue star has \( \mathrm{\lambda_{max} = 250\ nm} \) and luminosity \( \mathrm{5.0\times10^{28}\ W} \). Estimate its radius.
▶️ Answer / Explanation
Convert wavelength:
\( \mathrm{250\ nm = 250\times10^{-9}\ m} \)
Temperature:
\( \mathrm{T = \dfrac{2.90\times10^{-3}}{250\times10^{-9}} = 1.16\times10^{4}\ K} \)
Apply Stefan–Boltzmann law:
\( \mathrm{T^4 = 1.81\times10^{16}} \)
\( \mathrm{r = \sqrt{\dfrac{5.0\times10^{28}}{4\pi (5.67\times10^{-8})(1.81\times10^{16})}}} \)
Denominator \( \approx 1.29\times10^{10} \)
\( \mathrm{r = \sqrt{3.88\times10^{18}} = 1.97\times10^{9}\ m} \)
Radius ≈ \( \mathrm{2.0\times10^{9}\ m} \)
Example
A star has luminosity \( \mathrm{9\times10^{29}\ W} \). Its emitted spectrum peaks at \( \mathrm{150\ nm} \). Estimate the radius of the star.
▶️ Answer / Explanation
Convert wavelength:
\( \mathrm{150\ nm = 150\times10^{-9}\ m} \)
Temperature from Wien’s law:
\( \mathrm{T = \dfrac{2.90\times10^{-3}}{150\times10^{-9}} = 1.93\times10^{4}\ K} \)
Compute \( \mathrm{T^4} \):
\( \mathrm{T^4 = 1.39\times10^{17}} \)
Use Stefan–Boltzmann law:
\( \mathrm{r = \sqrt{\dfrac{9\times10^{29}}{4\pi(5.67\times10^{-8})(1.39\times10^{17})}}} \)
Denominator:
\( \mathrm{≈ 9.9\times10^{10}} \)
Finally:
\( \mathrm{r = \sqrt{\dfrac{9\times10^{29}}{9.9\times10^{10}}}} \)
\( \mathrm{r = \sqrt{9.09\times10^{18}} = 3.02\times10^{9}\ m} \)
Radius ≈ \( \mathrm{3.0\times10^{9}\ m} \)
