STEFAN-BOLTZMANN LAW & STELLAR RADII
Stefan-Boltzmann Law
- A star’s luminosity depends on two factors:
- Its surface temperature
- Its radius
- The relationship between these is known as the Stefan-Boltzmann Law, which states:
The total energy emitted by a black body per unit area per second is proportional to the fourth power of the absolute temperature of the body - It is equal to:
$
L=4 \pi r^2 \sigma \mathrm{T}^4
$
- Where:
- $L$ = luminosity of the star (W)
- $r=$ radius of the star $(m)$
- $\sigma=$ the Stefan-Boltzmann constant
- $T=$ surface temperature of the star (K)
Estimating the Radius of Stars
- The radius of a star can be estimated by combining Wien’s displacement law and the Stefan-Boltzmann law
- The procedure for this is as follows:
- Using Wien’s displacement law to find the surface temperature of the star
- Using the inverse square law of flux equation to find the luminosity of the star (if given the radiant flux and stellar distance)
- Then, using the Stefan-Boltzmann law, the stellar radius can be obtained
Worked example: Estimating the radius of a star
Betelguese is our nearest red giant star. It has a luminosity of $4.49 \times 10^{31} \mathrm{~W}$ and emits radiation with a peak wavelength of $850 \mathrm{~nm}$.
Calculate the ratio of the radius of Betelgeuse $r_B$ to the radius of the Sun $\mathrm{r}_{\mathrm{s}}$.
Radius of the sun $r_{\mathrm{s}}=6.95 \times 10^8 \mathrm{~m}$.
Answer/Explanation
Step 1:
Write down Wien’s displacement law
$
\lambda_{\max } T=2.9 \times 10^{-3} \mathrm{~m} \mathrm{~K}
$
Step 2: Rearrange Wien’s displacement law to find the surface temperature of Betelguese
$
T=\frac{2.9 \times 10^{-3}}{\lambda_{\max }}=\frac{2.9 \times 10^{-3}}{850 \times 10^{-9}}=3410 \mathrm{~K}
$
Step 3:
Write down the Stefan-Boltzmann law
$
\mathrm{L}=4 \pi r^2 \sigma \mathrm{T}^4
$
Step 4: $\quad$ Rearrange for $r$ and calculate the stellar radius of Betelguese
$
r_B=\sqrt{\frac{L}{4 \pi \sigma T^4}}=\sqrt{\frac{\left(4.49 \times 10^{31}\right)}{4 \pi \times\left(5.67 \times 10^{-8}\right) \times(3410)^4}}=6.83 \times 10^{11} \mathrm{~m}
$
Step 5:
Calculate the ratio $r_{\mathrm{B}} / r_{\mathrm{s}}$
$
\frac{r_B}{r_s}=\frac{6.83 \times 10^{11}}{6.95 \times 10^8}=983
$
Therefore, the radius of Betelguese is about 1000 times larger than the Sun’s radius
EMISSION SPECTRA
Emission Spectra
- Astronomers are very limited in how they can investigate objects in the space
- All of the techniques used involve analysing the light emitted from the star, or galaxy
- One of these techniques involves analysing the emission and absorption spectra of stars
- More details on this can be found in the revision notes “Line Spectra” in the Quantisation of Energy topic
- Elements in the star, predominantly hydrogen and helium, absorb some of the emitted wavelengths
- Therefore, characteristic lines are present when the spectrum is analysed
- When astronomers observe light from distant galaxies, they observe differences in the spectral lines to the light from the Sun
- The lines have the same characteristic pattern, meaning the element can still be easily identified, they just appear to be shifted sightly
- The lines in the spectra from distant galaxies show an increase in wavelength
- The lines are moved, or shifted, towards the red end of the spectrum
DOPPLER REDSHIFT
Redshift of EM Radiation
- Recall the Doppler effect is defined as:
The apparent change in wavelength or frequency of the radiation from a source due to its relative motion away from or toward the observer - On Earth, the Doppler effect of sound can be easily observed when sound waves moves past an observer at a notable speed
- In space, the Doppler effect of light can observed when spectra of distant stars and galaxies are observed, this is known as:
- Redshift if the object is moving away from the Earth, or
- Blueshift if the object is moving towards the Earth
- Redshift is defined as:
The fractional increase in wavelength (or decrease in frequency) due to the source and observer receding from each other - For non-relativistic galaxies, Doppler redshift can be calculated using:
$
\frac{\Delta \lambda}{\lambda}=\frac{\Delta f}{f}=\frac{v}{c}
$
- Where:
- $\Delta \lambda=$ shift in wavelength $(\mathrm{m})$
- $\lambda=$ wavelength emitted from the source $(m)$
- $\Delta f=$ shift in frequency $(\mathrm{Hz})$
- $f=$ frequency emitted from the source $(\mathrm{Hz})$
- $v=$ speed of recession $\left(\mathrm{m} \mathrm{s}^{-1}\right)$
- $c=$ speed of light in a vacuum $\left(\mathrm{m} \mathrm{s}^{-1}\right)$
Worked example: Redshift of a distant galaxy
The spectra below show dark absorption lines against a continuous visible spectrum.
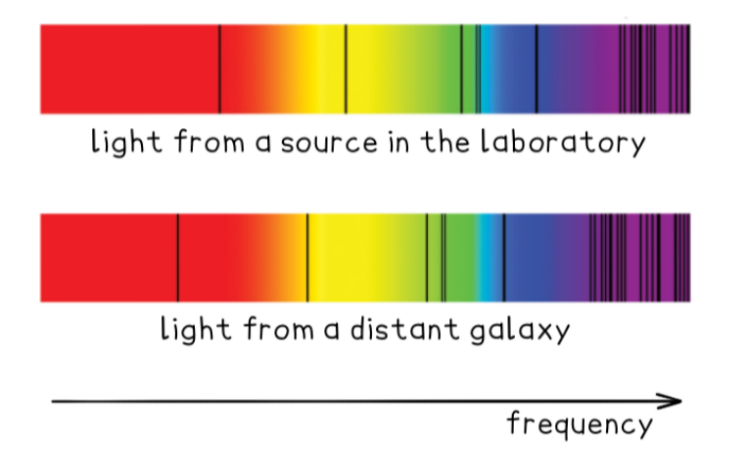
A particle line in the spectrum of light from a source in the laboratory has a frequency of $4.570 \times 10^{14} \mathrm{~Hz}$. The same line in the spectrum of light from a distant galaxy has a frequency of $4.547 \times 10^{14} \mathrm{~Hz}$. What speed is the distance galaxy moving in relation to the Earth? Is it moving towards or away from the Earth?
Answer/Explanation
Step 1:
Write down the known quantities
Emitted frequency, $f=4.570 \times 10^{14} \mathrm{~Hz}$
Shift in frequency, $\Delta f=(4.547-4.570) \times 10^{14}=-2.3 \times 10^{12} \mathrm{~Hz}$
Speed of light, $c=3.0 \times 10^8 \mathrm{~m} \mathrm{~s}^{-1}$
Step 2:
Write down the Doppler redshift equation
$
\frac{\Delta f}{f}=\frac{v}{c}
$
Step 3:
Rearrange for speed $v$, and calculate
$
v=\frac{c \Delta f}{f}=\frac{\left(3.0 \times 10^8\right) \times\left(2.3 \times 10^{12}\right)}{4.570 \times 10^{14}}=1.5 \times 10^6 \mathrm{~m} \mathrm{~s}^{-1}
$
Step 4: $\quad$ Write a concluding sentence
The observed frequency is less than the emitted frequency (the light from a laboratory source), therefore, the source is receding, or moving away, from the Earth at $1.5 \times 10^6 \mathrm{~m} \mathrm{~s}^{-1}$
Exam Tip
In your exam, be sure to emphasise that redshift means the wavelength of spectral lines increases towards the red end of the spectrum, do not say that the spectral lines become red, as this is incorrect.
An Expanding Universe
- After the discovery of Doppler redshift, astronomers began to realise that almost all the galaxies in the universe are receding
- This lead to the idea that the space between the Earth and the galaxies must be expanding
- This expansion stretches out the light waves as they travel through space, shifting them towards the red end of the spectrum
- The more red-shifted the light from a galaxy is, the faster the galaxy is moving away from Earth
- The expansion of the universe can be compared to dots on an inflating balloon
- As the balloon is inflated, the dots all move away from each other
- In the same way as the rubber stretches when the balloon is inflated, space itself is stretching out between galaxies
- Just like the dots, the galaxies move away from each other, however, they themselves do not move
