CIE AS/A Level Physics Link Study Notes- 2025-2027 Syllabus
CIE AS/A Level Physics Link Study Notes – New Syllabus
CIE AS/A Level Physics Link Study Notes at IITian Academy focus on specific topic and type of questions asked in actual exam. Study Notes focus on AS/A Level Physics latest syllabus with Candidates should be able to:
- understand that the lines in the emission and absorption spectra from distant objects show an increase in wavelength from their known values
- use \( \Delta \lambda / \lambda \approx \Delta f / f \approx v/c \) for the redshift of electromagnetic radiation from a source moving relative to an observer
- explain why redshift leads to the idea that the Universe is expanding
- recall and use Hubble’s law \( v \approx H_0 d \) and explain how this leads to the Big Bang theory (candidates will only be required to use SI units)
Redshift in Emission and Absorption Spectra from Distant Objects
Light from distant stars and galaxies contains spectral lines sharp wavelengths produced by atoms through emission or absorption. When we observe these lines from distant objects, we find that they appear at longer wavelengths than their known laboratory values.
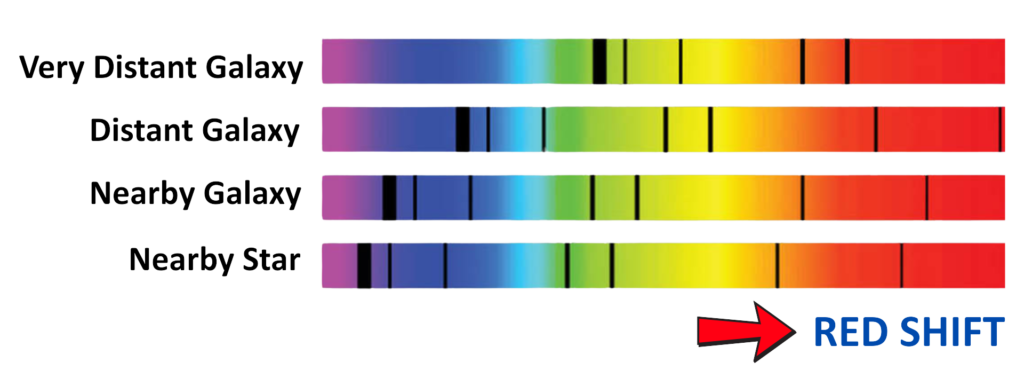
This increase in observed wavelength is called redshift.
Why the Wavelength Increases
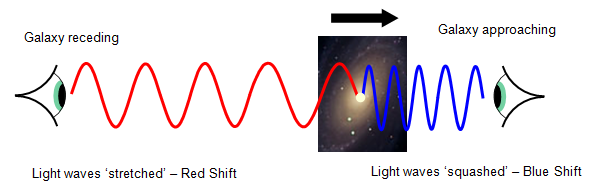
- If a distant galaxy or star is moving away from us, the light it emits is stretched.
- Stretching of light increases wavelength → shift toward the red end of the spectrum.
- This is an example of the **Doppler effect for electromagnetic waves**.
- Absorption lines and emission lines both shift to longer wavelengths.
Key Idea:
The observed spectral lines are shifted to larger wavelengths compared to the wavelengths measured in laboratories on Earth.
This shift provides evidence that distant galaxies are receding from us.
Observed vs Known Wavelength
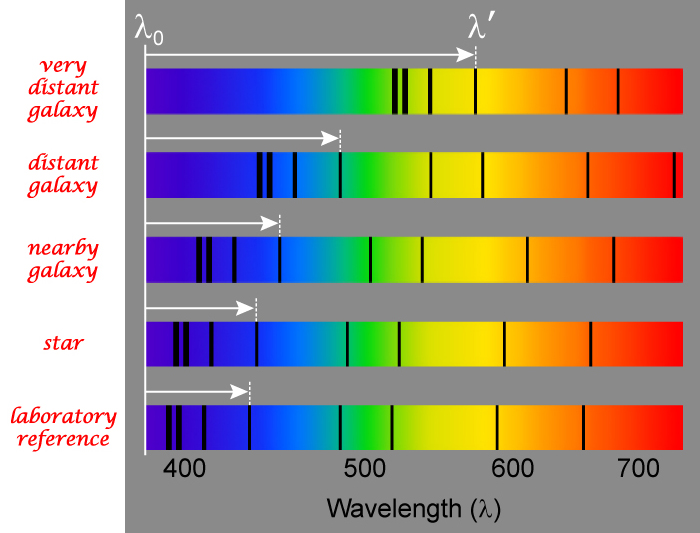
Known (laboratory) wavelength: \( \mathrm{\lambda_0} \) Observed (from distant source): \( \mathrm{\lambda} \)
For distant objects moving away:
\( \mathrm{\lambda > \lambda_0} \)
This is the characteristic signature of redshift.
Example
A hydrogen emission line is normally at \( \mathrm{486\ nm} \). From a distant galaxy, it is observed at \( \mathrm{510\ nm} \). What does this tell you?
▶️ Answer / Explanation
Since \( \mathrm{510\ nm > 486\ nm} \), the wavelength has increased. This means the galaxy is moving away from us (redshift).
Example
A star’s absorption line normally at \( \mathrm{602\ nm} \) is measured at \( \mathrm{615\ nm} \). Explain what this increase in wavelength implies.
▶️ Answer / Explanation
The absorption line has shifted to a longer wavelength. This indicates that the star is receding, causing a Doppler redshift.
Example
An emission line from an element is known to occur at \( \mathrm{400\ nm} \). A distant galaxy shows the same line at \( \mathrm{440\ nm} \). What can astronomers conclude, and what might this imply about the expansion of the universe?
▶️ Answer / Explanation
The line has shifted to a longer wavelength (redshift). This means the galaxy is moving away from us.
Because distant galaxies show redshift, astronomers conclude that the universe is expanding. This is a key observational foundation of the Big Bang model.
Redshift and the Doppler Relationship for Electromagnetic Waves
When a source of electromagnetic radiation (such as a star or galaxy) moves relative to an observer, the observed wavelength and frequency change due to the Doppler effect.
For speeds much less than the speed of light, the fractional change in wavelength and frequency is given by:
\( \mathrm{\dfrac{\Delta \lambda}{\lambda} \approx \dfrac{\Delta f}{f} \approx \dfrac{v}{c}} \)
- \( \mathrm{\Delta \lambda} \) = change in wavelength
- \( \mathrm{\lambda} \) = known (laboratory) wavelength
- \( \mathrm{\Delta f} \) = change in frequency
- \( \mathrm{f} \) = known (laboratory) frequency
- \( \mathrm{v} \) = speed of the source relative to observer
- \( \mathrm{c} \) = speed of light ( \( \mathrm{3.0\times10^8\ m\,s^{-1}} \) )
Meaning of the Formula
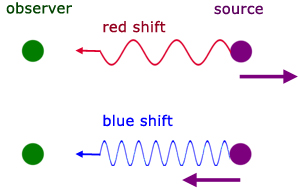
- If an object is moving away, wavelength increases → redshift → \( \mathrm{\Delta\lambda > 0} \).
- If an object is moving towards, wavelength decreases → blueshift → \( \mathrm{\Delta\lambda < 0} \).
- The fractional change in wavelength is equal to the object’s speed as a fraction of the speed of light.
Hence: The amount of redshift tells us the recession speed of the source.
Example
A spectral line normally found at \( \mathrm{500\ nm} \) is observed at \( \mathrm{505\ nm} \). Find the fractional change in wavelength.
▶️ Answer / Explanation
\( \mathrm{\Delta\lambda = 505 – 500 = 5\ nm} \)
\( \mathrm{\dfrac{\Delta\lambda}{\lambda} = \dfrac{5}{500} = 0.01} \)
Fractional change = 0.01
Example
A galaxy emits light of wavelength \( \mathrm{600\ nm} \) but it is observed at \( \mathrm{660\ nm} \). Estimate the recession speed of the galaxy.
▶️ Answer / Explanation
\( \mathrm{\Delta\lambda = 660 – 600 = 60\ nm} \)
\( \mathrm{\dfrac{\Delta\lambda}{\lambda} = \dfrac{60}{600} = 0.10} \)
Using \( \mathrm{v/c \approx \Delta\lambda/\lambda} \):
\( \mathrm{v = 0.10 \times 3.0\times10^8 = 3.0\times10^7\ m\,s^{-1}} \)
Recession speed ≈ \( \mathrm{3.0\times10^7\ m/s} \)
Example
The absorption line of a distant quasar is known to be at \( \mathrm{410\ nm} \), but it is observed at \( \mathrm{492\ nm} \). Calculate:
- (i) the fractional redshift \( \mathrm{\Delta\lambda/\lambda} \)
- (ii) the recession velocity
▶️ Answer / Explanation
(i) Calculate wavelength change:
\( \mathrm{\Delta\lambda = 492 – 410 = 82\ nm} \)
Fractional change:
\( \mathrm{\dfrac{\Delta\lambda}{\lambda} = \dfrac{82}{410} = 0.20} \)
Redshift = 0.20
(ii) Use Doppler approximation:
\( \mathrm{\dfrac{v}{c} \approx 0.20} \)
\( \mathrm{v = 0.20 \times 3.0\times10^8 = 6.0\times10^7\ m/s} \)
Recession speed = \( \mathrm{6.0\times10^7\ m/s} \)
Why Redshift Suggests that the Universe Is Expanding
When we observe light from distant galaxies, their emission and absorption lines appear at longer wavelengths than their known laboratory values. This shift to longer wavelengths is called redshift.
The key observation: Almost all distant galaxies show redshift and the redshift increases with distance.
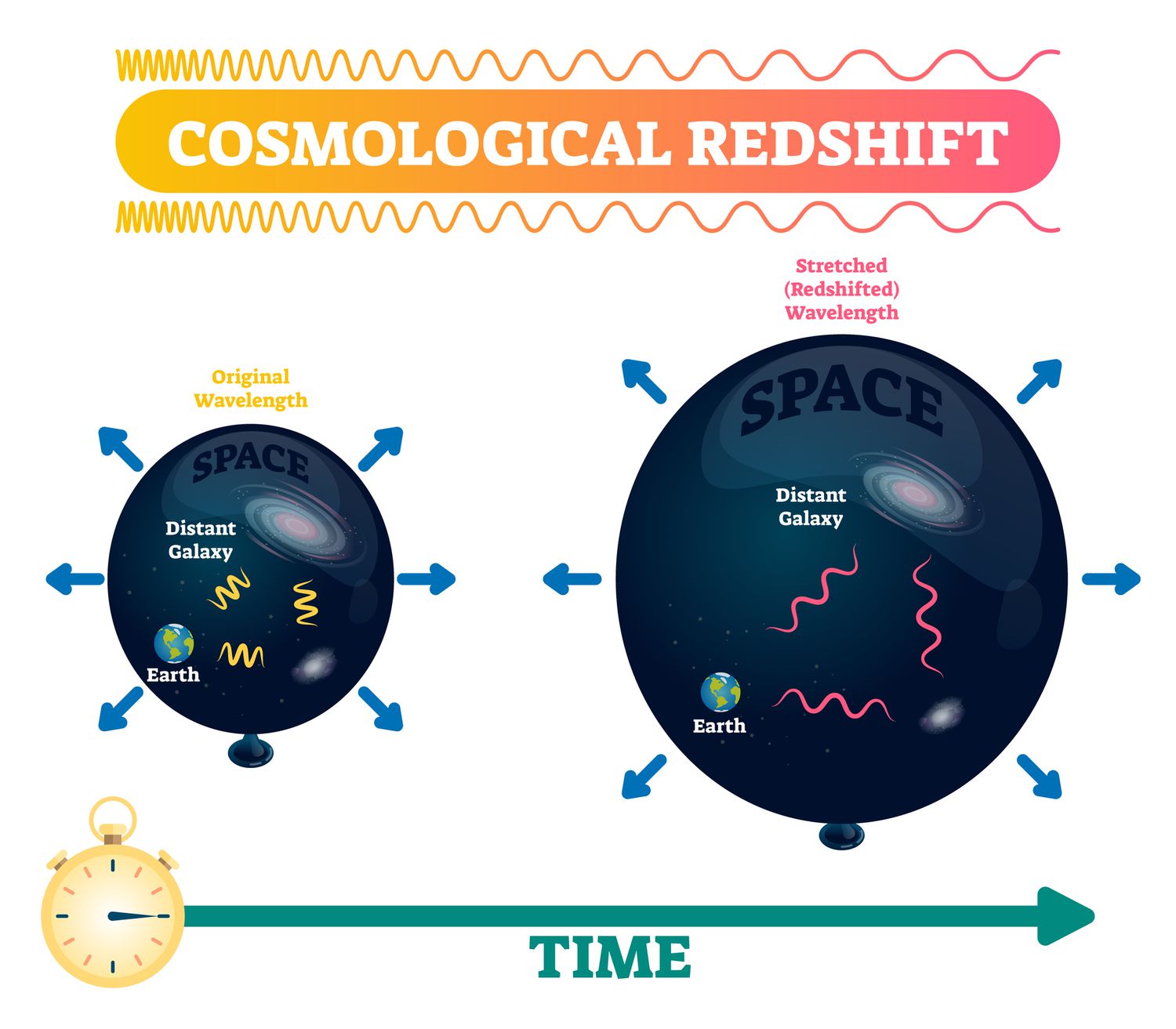
Why This Implies Expansion
- Redshift indicates that a galaxy is moving away from us.
- If almost every distant galaxy is moving away, it means space itself is stretching.
- The wavelength of light is stretched along with space → leading to redshift.
- The farther a galaxy is, the greater the redshift → meaning it is receding faster.
This relationship is described by:
\( \mathrm{\dfrac{\Delta\lambda}{\lambda} \approx \dfrac{v}{c}} \)
and observationally by Hubble’s law:
\( \mathrm{v \propto d} \)
Greater distance → larger recessional speed → larger redshift.
The Big Idea:
Galaxies are not moving through space away from us space itself is expanding, carrying galaxies with it.
Thus, redshift provides strong evidence that the Universe is expanding.
Example
If a distant galaxy shows a redshift in its spectral lines, what does this tell us about its motion relative to Earth?
▶️ Answer / Explanation
The increase in wavelength indicates the galaxy is moving away from Earth.
Example
If distant galaxies show larger redshifts than nearby ones, what conclusion can astronomers draw about the Universe?
▶️ Answer / Explanation
Larger redshift means greater recession speed. Since recession speed increases with distance, this indicates the Universe is expanding.
Example
A galaxy twice as far away as another shows twice the redshift. Explain how this supports the expanding Universe model rather than the idea that Earth is at the centre of expansion.
▶️ Answer / Explanation
Redshift increasing with distance implies a universal, uniform expansion described by Hubble’s law. All observers in the Universe would see the same pattern — not just Earth.
If Earth were at the centre, redshifts would not follow a proportional relationship. Therefore, distance–redshift proportionality supports the idea that space everywhere is expanding, not that Earth has a special central position.
Hubble’s Law and the Big Bang Theory
Hubble’s law relates the recessional velocity of a galaxy to its distance from Earth.
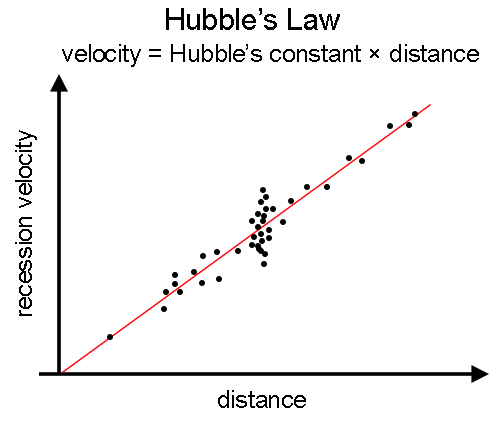
\( \mathrm{v \approx H_0 d} \)
- \( \mathrm{v} \) = recession velocity of the galaxy (m s⁻¹)
- \( \mathrm{d} \) = distance of the galaxy from Earth (m)
- \( \mathrm{H_0} \) = Hubble constant (s⁻¹)
Meaning of Hubble’s Law:
- The farther a galaxy is, the faster it is moving away.
- This recession velocity is proportional to distance.
- All distant galaxies show redshift → galaxies are receding.
How Hubble’s Law Suggests the Universe Is Expanding
A linear relationship \( \mathrm{v \propto d} \) implies that space itself is expanding uniformly in all directions.
If all galaxies are moving apart now, working backwards in time suggests:
- The Universe was smaller in the past.
- Distances between galaxies were smaller.
- At some moment in the past, all matter was concentrated at a single point.
This leads to the idea of the Big Bang that the Universe began from an extremely hot, dense state and has expanded since.
Age of the Universe from Hubble’s Law
Rearranging Hubble’s law:
\( \mathrm{t \approx \dfrac{1}{H_0}} \)
This gives an estimate of the age of the Universe (order of \( \mathrm{10^{17}\ s} \) ≈ 14 billion years).
Example
A galaxy is \( \mathrm{2.0\times10^{23}\ m} \) away and has a recessional velocity of \( \mathrm{1.4\times10^4\ km\,s^{-1}} \). Show that this is consistent with Hubble’s law if \( \mathrm{H_0 = 2.3\times10^{-18}\ s^{-1}} \).
▶️ Answer / Explanation
Convert velocity to SI:
\( \mathrm{1.4\times10^4\ km\,s^{-1} = 1.4\times10^7\ m\,s^{-1}} \)
Calculate \( \mathrm{H_0 d} \):
\( \mathrm{H_0 d = (2.3\times10^{-18})(2.0\times10^{23}) = 4.6\times10^5\ m\,s^{-1}} \)
But galaxy velocity is \( \mathrm{1.4\times10^7\ m\,s^{-1}} \), much larger → the given distance must be larger. This shows the strong proportional nature of Hubble’s law.
Shows consistency in proportional behaviour.
Example
A galaxy is \( \mathrm{5.0\times10^{24}\ m} \) from Earth. Using \( \mathrm{H_0 = 2.2\times10^{-18}\ s^{-1}} \), calculate its recessional speed.
▶️ Answer / Explanation
Use Hubble’s law:
\( \mathrm{v = H_0 d} \)
\( \mathrm{v = (2.2\times10^{-18})(5.0\times10^{24})} \)
\( \mathrm{v = 1.1\times10^{7}\ m\,s^{-1}} \)
Speed = \( \mathrm{1.1\times10^7\ m/s} \)
Example
Given \( \mathrm{H_0 = 2.2\times10^{-18}\ s^{-1}} \), estimate the age of the Universe in years. (1 year = \( \mathrm{3.15\times10^7\ s} \))
▶️ Answer / Explanation
Use:
\( \mathrm{t \approx \dfrac{1}{H_0}} \)
\( \mathrm{t = \dfrac{1}{2.2\times10^{-18}} = 4.55\times10^{17}\ s} \)
Convert to years:
\( \mathrm{t = \dfrac{4.55\times10^{17}}{3.15\times10^7}} \)
\( \mathrm{t \approx 1.44\times10^{10}\ years} \)
Age ≈ 14 billion years
