Using a vector triangle to represent forces in Equilibrium
(1) Two forces in equilibrium
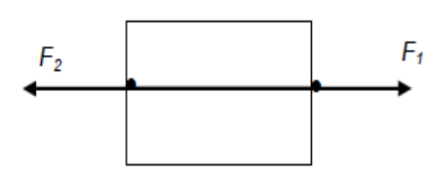
Consider two forces acting on a crate is in equilibrium,
Conclusion:
They must act along the same line of action (collinear), be equal in magnitude and opposite in direction.
$
\begin{array}{ll}
\Sigma F_x=0 ; & F_1-F_2=0 \\
& F_1=F_2 \text { (no resultant force) }
\end{array}
$
(2) Three forces in equilibrium
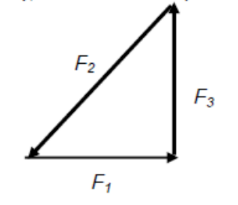
Consider three forces acting on a crate is in equilibrium,
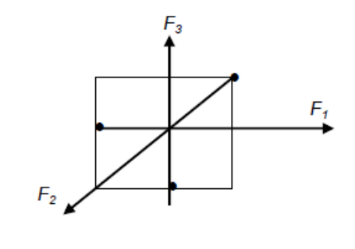
Conclusion:
1) They must act on the same plane (coplanar)
2) They form a closed triangle.
3) They must all act through the same point (concurrent),
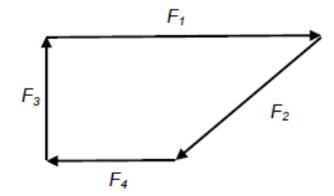
(3) Four or more forces in equilibrium
Consider four or more forces acting on a crate is in equilibrium,
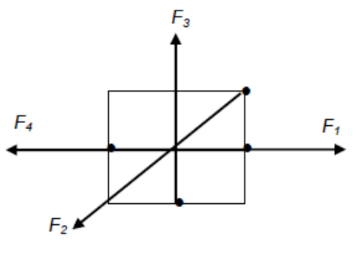
Conclusion:
1) They must act on the same plane (coplanar)
2) They form a closed polygon
3) They must all act through the same point.
Centre of Gravity
- The weight of an object may be taken as acting at one point known as the centre of gravity.
- You could think of that point as the position where all the mass of the object could be thought to be concentrated.
The centre of gravity of an object is the point through which the weight of the object is taken to act.
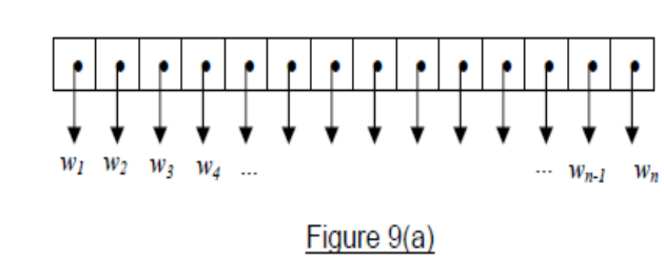
The weights $w$ of $n$ individual particles of an object are effectively parallel to each other as seen in Figure in 9(a).
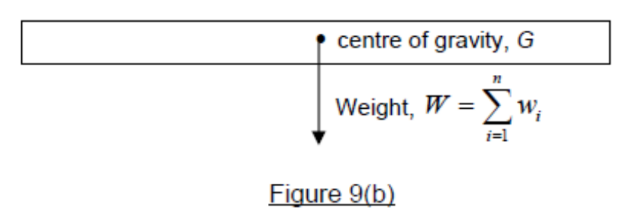
The weight $W$ of an object is the resultant force of all the individual weights $w$ of its particles in the object and is directed towards the centre of the Earth. The centre of gravity, $G$ of a rigid body (Figure $9 \mathrm{~b}$ ) is the single point through which the weight of the object appears to act.
The factors affecting position of centre of gravity are (1) distribution of the masses; and (2) the acceleration of free fall $g$.
Hence, if the distribution of masses and $g$ remain constant on all parts of the objects, the centre of gravity will coincide with the centre of mass of the object.
A couple
- In physics, couple is a pair of equal parallel forces that are opposite in direction. Couples produce or prevent the turning of a body.
- The forces used to turn the steering wheel of a car constitute a couple; each hand exerts a force, parallel but opposite in direction, yet they work together to achieve the same goal.
- It tends to produce rotation only. There is no linear change in motion due to net/resultant force being zero. The pair of forces is non-concurrent. (i.e. their lines of actions do not pass through the a single common point)
The moment of a Force
• The moment of a force about a pivot is the product of that force and the perpendicular distance between the line of action of the force and the pivot.
Moment of a force (calculation)
• The moment of a force can be worked out using the formula:
• Moment = force applied × perpendicular distance from the pivot.
• If the magnitude of the force is F Newtons and the perpendicular distance is d metres then:
Moment = Fd
The Torque of a couple
• When a driver turns a steering wheel, he exerts two equal but opposite forces on it. The two forces form a couple. The turning effect of a couple is the sum of moment of the two forces. The moment of a couple is called a torque.
• The torque of a couple is the product of one of the forces and the perpendicular distance between their lines of action.
In other words, Torque is…
• Torque is a measure of how much a force acting on an object causes that object to rotate.
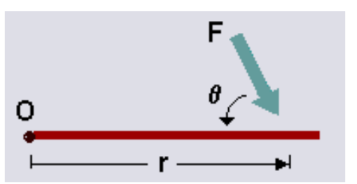
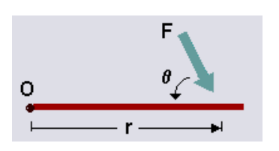
• The object rotates about an axis, which we will call the pivot point, and will label ‘O’.
• We will call the force ‘F’. The distance from the pivot point to the point where the force acts is called the moment arm, and is denoted by ‘r’. Note that this distance, ‘r’, is also a vector, and points from the axis of rotation to the point where the force acts. (Refer to Figure for a pictorial representation of these definitions.)
Calculation of Torque
• Torque is calculated using the equation $\mathbf{T}=\mathbf{r} \times \mathbf{F}=\mathbf{r} F \sin \theta$.
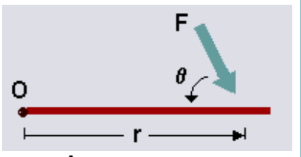
• In other words, torque is the cross product between the distance vector (the distance from the pivot point to the point where force is applied) and the force vector, ‘a’ being the angle between r and F.
• Using the right hand rule, we can find the direction of the torque vector. If we put our fingers in the direction of r, and curl them to the direction of F, then the thumb points in the direction of the torque vector.
When there is no resultant force and no resultant torque, a system is in equilibrium
A system is in equilibrium
• The state of a body or physical system that is at rest or in constant and unchanging motion.
• If a system is in static equilibrium, there are no net forces and no net torque in the system.
• If a system is in stable equilibrium, small disturbances to the system cause only a temporary change before it returns to its original state.
Two conditions must be satisfied for static equilibrium to take place for a rigid body.

a) Resultant force $=$ zero
The vector sum of all external rorces acting on a rigid body must be zero i.e. no net/resultant force
$
\Sigma F=0
$
b) Resultant torque $=$ zero .
The vector sum of all external torques acting on a rigid body must be zero i.e. No net/resultant torque, OR
Mathematically,
$
\Sigma \tau=0
$
Principle of moments
State the Principle of Moments
If a body is in equilibrium the sum of the clockwise moments is equal to the sum of the anticlockwise moments.
Principle of moments for a body in equilibrium An object is in equilibrium if the sum of all anticlockwise moments about the pivot is equal to the sum of all clockwise moments about the same pivot.
All anti-clockwise moments can be taken to be positive and clockwise moments to be negative or vice versa.
