Density and Pressure
Density is defined as the mass per unit volume of a substance:
$
\text { density }=\frac{\text { mass }}{\text { volume }}
$
Pressure is defined as the normal force acting per unit cross-sectional area:
$
\text { pressure }=\frac{\text { force }}{\text { area }}
$
Pressure in a fluid increases with depth:
$
p=\rho g h
$
Derive from the definitions of pressure and density, the equation p = ρgh
It is a well-known fact that pressure increases with depth of liquid. The relation between the pressure $p$ due to a fluid (liquid or gas) at depth $h$ is given by the equation
$
p=\rho g h,
$
where $\rho$ is the density of the fluid and $g$ is the acceleration of free fall. The equation can be derived as follows:
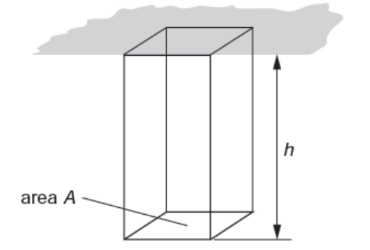
Consider a flat horizontal surface at a depth $h$ in a fluid of density $\rho$. Then,
$
\begin{aligned}
\text { mass of fluid on area } & =\text { density } \times \text { volume } \\
& =\rho A h
\end{aligned}
$
and weight of fluid on area $=\rho$ Ahg .
This weight of fluid produces a pressure $p$ on the area given by
$
\begin{aligned}
\text { pressure } p & =\frac{\text { force }}{\text { area }} \\
& =\frac{\rho g A h}{A} \\
p & =\rho g h .
\end{aligned}
$
Note that this equation allows the pressure due to the fluid to be calculated. It should be remembered that the actual pressure at depth $h$ in a liquid would be given by
pressure $=\rho g h+$ atmospheric pressure at liquid surface
Sample problem 1
- Calculate the pressure on an inspection harch $7 \mathrm{~m}$ diameter located on the bottom of a tank when it is filled with oil of density $875 \mathrm{Kgm}^{-3}$ to a depth of 7 metres.
Answer/Explanation
Solution
The Pressure at the bottom of the tank is given by $p=\rho g h$ $\rho=875 \mathrm{Kgm}^{-3}, \mathrm{~h}=7 \mathrm{~m}, \mathrm{~g}=9.8 \mathrm{~ms}^{-2}$
$p=\rho g h$
$=875 \times 9.8 \times 7$
$=60.086 \mathrm{kPa}$
