Transverse Waves
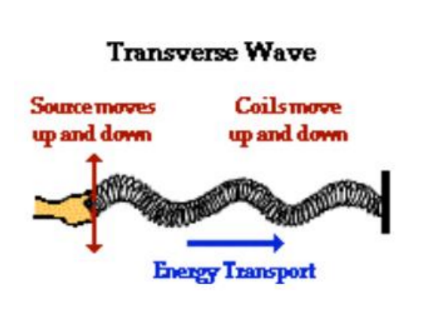
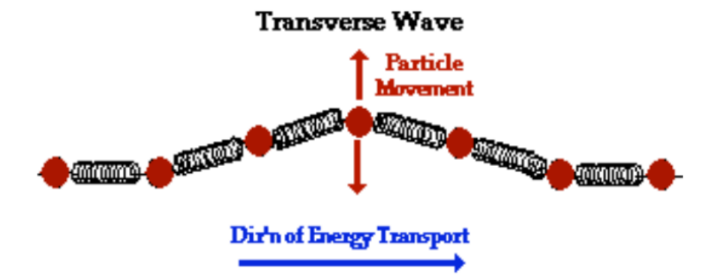
• Transverse waves propagate in a direction perpendicular to the direction of vibration.
Longitudinal Waves
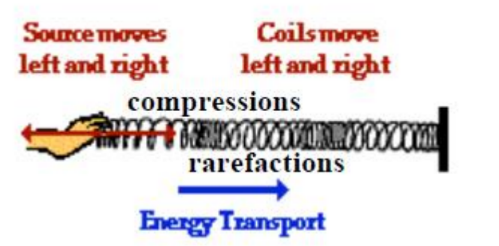
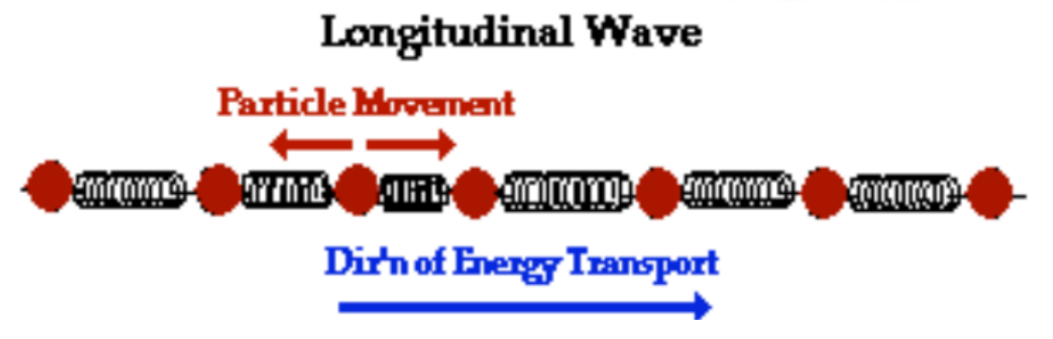
• Longitudinal waves propagate in a direction parallel to the direction of vibration.
Describing Waves
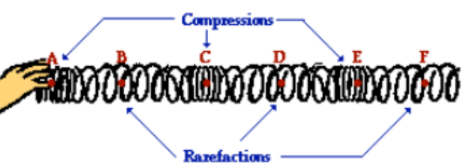
- Crests and troughs
- High points and low points that characterise transverse waves only. For longitudinal waves, compressions and rarefactions are used.
- Amplitude, A, SI Unit: metre (m)
- The value of the maximum displacement from the rest of central position in either direction.
displacement in metres
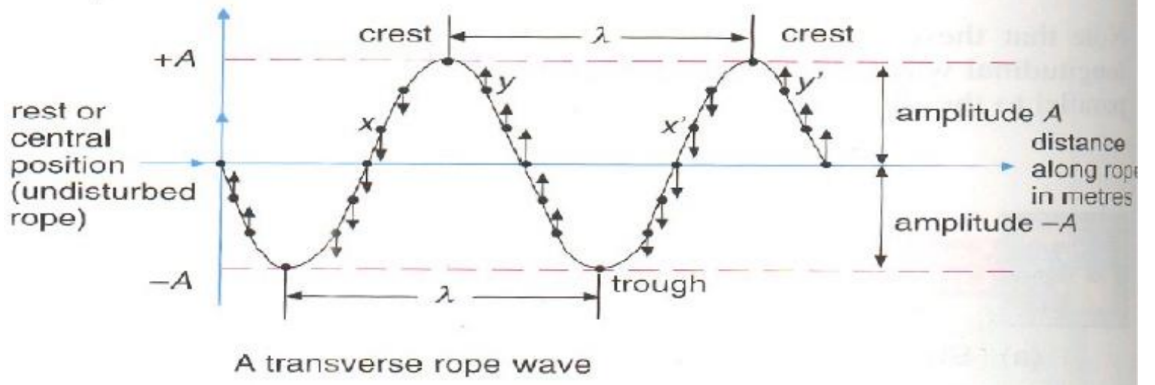
- Wavelength, $\lambda$, SI Unit : metre (m)
- The shortest distance between any two points on a wave that are in phase. The two easiest points to choose for a distance of one wavelength are two successive crests or troughs.
displacement in metres
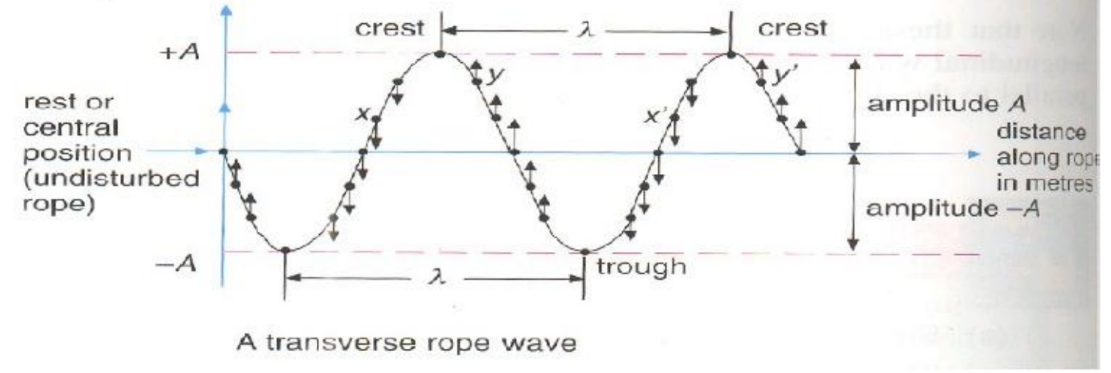
- Phase
- Two points (such as $x \& x^{\prime}$, and y \& y’) are said to be in phase because that are moving in the same direction with the same speed and having the same displacement from the rest position. Any two crests or trough are in phases.
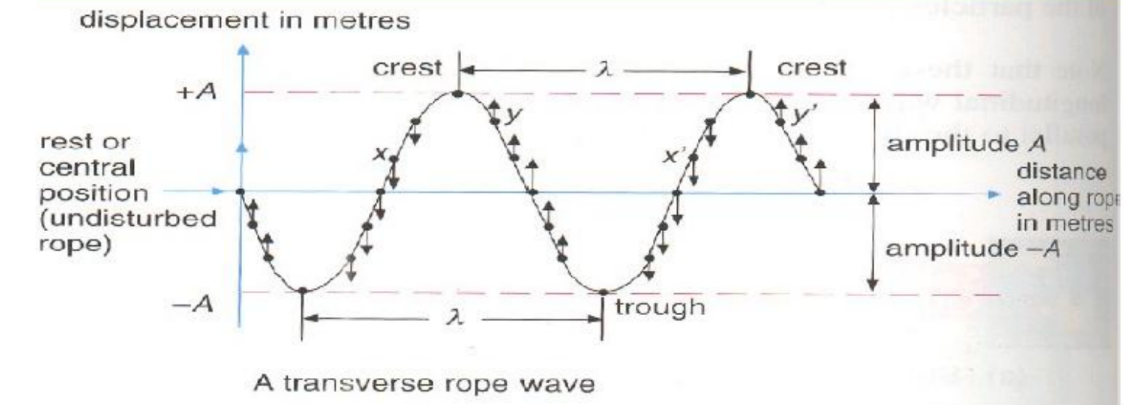
Describing Waves – Phase difference
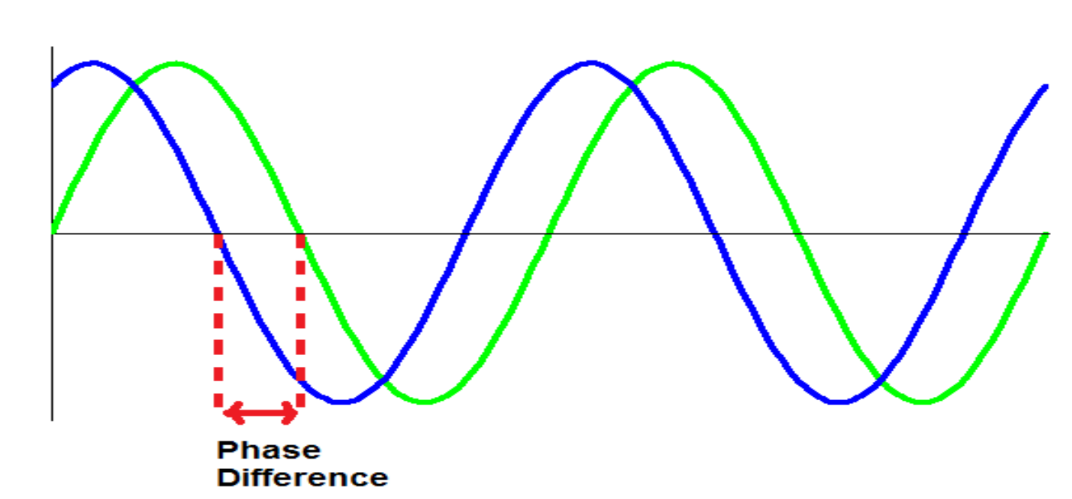
A term used to describe the relative positions of the crests or troughs of two waves of the same frequency is phase. When the crests and troughs of the two waves are aligned, the waves are said to be in phase. When a crest is aligned with a trough, the waves are out of phase. When used as a quantitative measure, phase has the unit of angle (radians or degrees). Thus, when waves are out of phase, one wave is half a cycle behind the other. Since one cycle is equivalent to $2 \pi$ radians or $360^{\circ}$, the phase difference between waves that are exactly out of phase is $\pi$ radians or $180^{\circ}$.
Consider Figure : in which there are two waves of the same frequency, but with a phase difference between them. The period $T$ corresponds to a phase angle of $2 \pi$ rad or $360^{\circ}$. The two waves are out of step by a time $t$. Thus, phase difference is equal to $2 \pi(t / T) \mathrm{rad}=360(t / T)^{\circ}$. A similar argument may be used for waves of wavelength $\lambda$ which are out of step by a distance $x$. In this case the phase difference is $2 \pi(x / \lambda)$ rad $=360(x / \lambda)^{\circ}$.
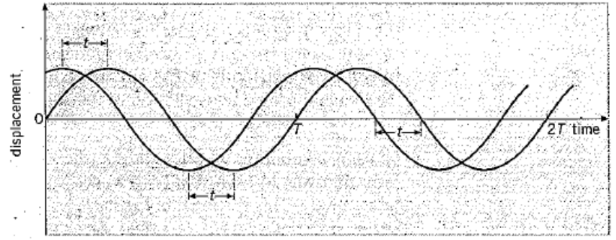
$
\Phi=2 \prod \frac{x}{\lambda} \text { OR } \Phi=360^{\circ} \frac{x}{\lambda}
$
Where $\phi$ is phase difference, $\mathrm{x}$ is distance, $\lambda$ is the wavelength.
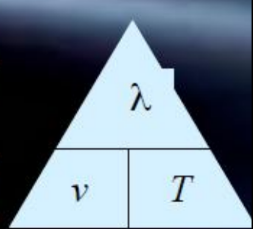
The wave equation and principle
- Speed = distance/time
- Wavelength is the distance moved by the wave in one cycle i.e distance
- Time = period = 1/frequency
- So speed = wavelength/period
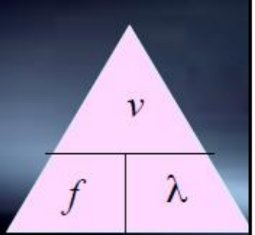
Speed $=$ wavelength $x$ frequency, i.e $\nabla=1$
The Wave Equation
The relationship of $v, \lambda \& f$
$
v=f \lambda
$
The relationship of $v, \lambda \& T$
Since $T=1 / f$
$v=\frac{\lambda}{T}$
$\begin{aligned} & v=f \lambda \\ & f=v / \lambda \\ & \lambda=v / f\end{aligned}$
$\begin{aligned} & f=1 / T \\ & v=\lambda / T \\ & \lambda=v T \\ & T=1 / f \\ & T=\lambda v\end{aligned}$
Example 1
Visible light has wavelengths between $400 \mathrm{~nm}$ and $700 \mathrm{~nm}$, and its speed in a vacuum is $3.0 \times 10^8 \mathrm{~m} \mathrm{~s}^{-1}$
What is the maximum frequency of visible light?
Answer/Explanation
Solution:
From $v=f \lambda$, the frequency $f=\frac{v}{\lambda}$, i.e. $f$ is inversely proportional to $\lambda$.
For maximum frequency, minimum wavelength should be used.
Hence, $\quad f_{\max }=\frac{v}{\lambda_{\min }}=\frac{3 \times 10^8 \mathrm{~m} \mathrm{~s}^{-1}}{400 \times 10^{-8} \mathrm{~m}}=7.5 \times 10^{14} \mathrm{~Hz}$
Example 2
A sound wave of frequency $400 \mathrm{~Hz}$ is travelling in a gas at a speed of $320 \mathrm{~m} \mathrm{~s}^{-1}$.
What is the phase difference between two points $0.2 \mathrm{~m}$ apart in the direction of travel?
Answer/Explanation
Solution:
$
\begin{aligned}
& \text { Wavelength, } \lambda=\frac{v}{f}=\frac{320 \mathrm{~m} \mathrm{~s}^{-1}}{400 \mathrm{~Hz}}=0.80 \mathrm{~m} \\
& \frac{\phi}{2 \pi}=\frac{x}{\lambda}=\frac{0.2 \mathrm{~m}}{0.8 \mathrm{~m}}=\frac{1}{4} \quad \rightarrow \quad \phi=\frac{\pi}{2} \mathrm{rad}
\end{aligned}
$
Example 3
Two boats are anchored 4 metres apart. They bob up and down every 3 seconds, but when one is up the other is down. There are never any wave crests between the boats. Calculate the speed of the waves.
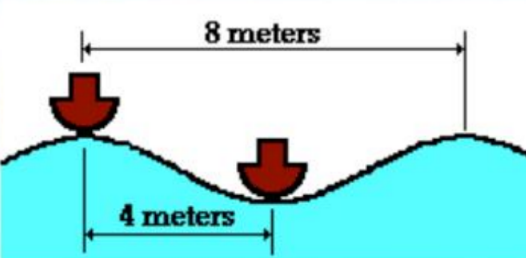
Period, $T=(3 \times 2) \mathrm{s}=6 \mathrm{~s}$
Wavelength, $\lambda=8 \mathrm{~m}$
Speed, $v=\lambda T=(8 / 6) \mathrm{m} / \mathrm{s}=1.33 \mathrm{~m} / \mathrm{s}$
Ripple Tank (Wave production)
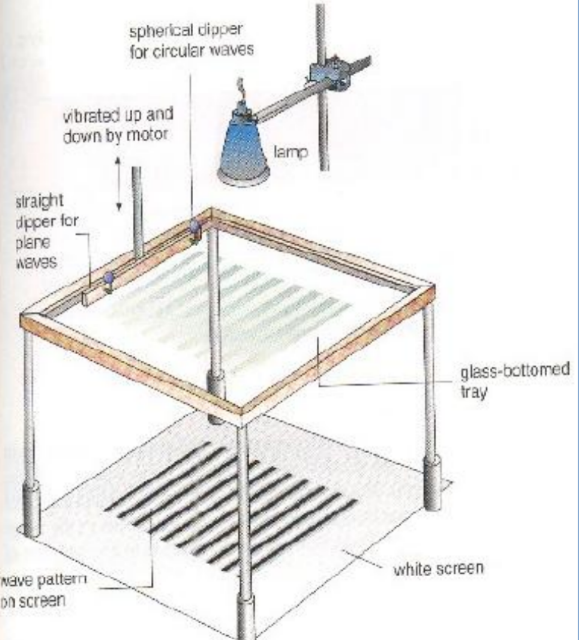
- The Structure
- A shallow glass-bottomed tray;
- A light source directly above the tray; and
- A white screen beneath the tray used to capture the shadows formed when water waves traverse the tray.
- Production of waves
- Plane waves by using the straight dipper
- Circular waves by spherical dipper
Energy is transferred by a progressive wave
Wave Motion
- There are also two other ways to classify waves – by their motion. A wave in which energy is transferred from one place to another as a result of its motion is called a progressive wave.
- For example : An ultraviolet light wave, which transfers energy from the sun to the skin of people lying on the beach, for instance, is a progressive wave. In general, waves that move from one point to another transfer some kind of energy.
- In a progressive wave, the shape of the wave itself, is what is transferred, not the actual components of the medium.
Look at this animated example

• This animation of a dog on a leash shows a progressive wave transferring energy from the boy to the dog, which end up getting flipped through the air.
Show an understanding that energy is transferred due to a progressive wave.
- Oscillation (or oscillatory motion) refers to the to-and-fro motion of a particle about an equilibrium position.
The oscillatory motion of the particle is a continuous exchange of potential and kinetic energy of the particle.
- Wave refers to the combined motion of a series of linked-particles, each of which is originally at rest at its respective equilibrium position.
Starting from the oscillation of the first particle about its equilibrium position, the energy of the oscillation is passed to the second particle, which in turn is passed to the third particle and subsequent particles in the series of linked-particles.
So wave motion is the motion of energy passed from one particle to the next in a series, through oscillatory motion of these particles, in sequence.
Examples:
(1) Sound wave:
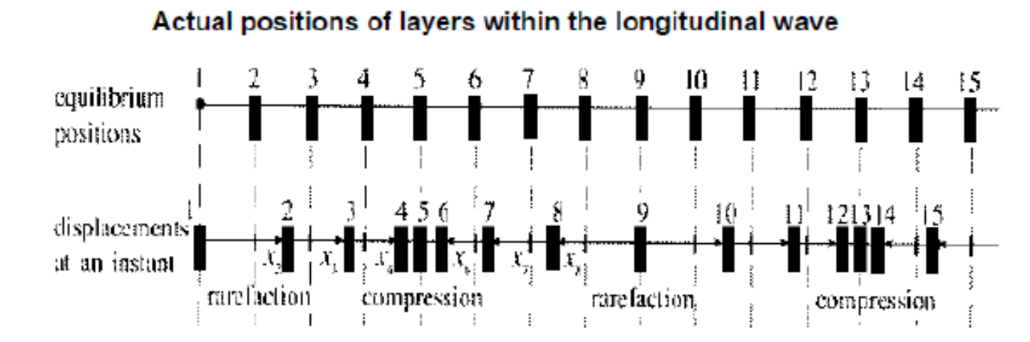
When a sound wave is propagated from a tuning fork to an ear of a person some distance away, the vibration of the fork sets the air layer next to it into vibration.
The second layer of air is then set into vibration by the transfer of energy from the first layer.
This transfer of energy continues for subsequent layers until the layer of air next to the ear is also set into vibration, which in turn vibrates the ear-drum of the ear, enabling the person to hear the sound originated from the tuning fork.
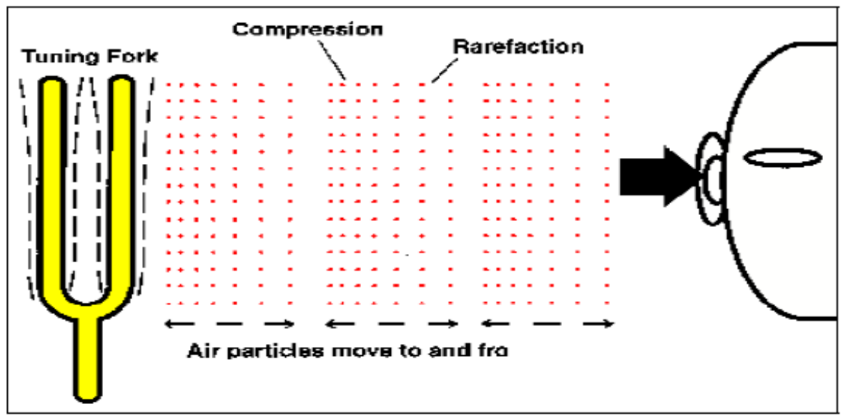
There is no net transfer of air particles from the tuning fork to the ear. The ear-drum in the ear can vibrate because energy has been transferred to it from the tuning fork, through the sequential vibration of the layers of air between the tuning fork and the ear. (Diagram above)
This sequential vibration of the layers of air forms regions of compression (where air layers are closer to each other) and regions of rarefaction (where air layers are further apart). The one-way movement of such regions from the tuning fork to the ear signifies the propagation of sound wave energy.
(2) Wave in a rope:
The wave travelling in a rope may originate from the vibration of the first particle at one end of the rope.
The energy of the vibrating first particle is transferred to the second particle, setting it into vibration.
This transfer of energy continues to subsequent particles in the rope until it reaches the other end of the rope.
(3) Water wave:
The energy of the vibrating water molecules is transferred to subsequent molecules along the surface of water, causing these molecules further from the vibrating source to be set into up-down motion.
The examples (1), (2) and (3) are examples of progressive waves, where energy is transferred from one region to another region through sequential vibration of a series of linked-particles.
The energy of a first vibrating particle is propagated along a series of linked-particles to another region. Sound energy is propagated from the tuning fork to the ear, energy from one end of a rope is propagated to the other end, and energy from one region of water surface next to a vibrating source is propagated to another region in the ripple tank.
Intensity of the Wave
One of the characteristics of a progressive wave is that it carries energy. The amount of energy passing through unit area per unit time is called the intensity of the wave. The intensity is proportional to the square of the amplitude of a wave. Thus, doubling the amplitude of a wave increases the intensity of the wave by a factor of four. The intensity also depends on the frequency: intensity is proportional to the square of the frequency.
For a wave of amplitude $A$ and frequency $f$, the intensity $I$ is proportional to $A^2 f^2$.
If the waves from a point source spread out equally in all directions, we have what is called a spherical wave. As the wave travels further from the source, the energy it carries passes through an increasingly large area. Since the surface area of a sphere is $4 \pi r^2$, the intensity is $W / 4 \pi r^2$, where $W$ is the power of the source. The intensity of the wave thus decreases with increasing distance from the source. The intensity $I$ is proportional to $1 / r^2$, where $r$ is the distance from the source.
This relationship assumes that there is no absorption of wave energy.
Recall and use the relationship, intensity $\propto$ (amplitude) ${ }^2$.
Intensity, $I$, is the rate of incidence of energy per unit area normal to the direction of incidence.
The rate of incidence of energy can be regarded as power.
The plane of the area, which the wave energy is incident onto, has to be normal (perpendicular) to the direction of the incidence of the wave energy.
The unit of intensity is $\mathbf{W ~} \mathbf{m}^{-2}$.
Intensity on an area $A$ can be expressed as
$
I=\frac{P}{A}
$
where $P$ is the power incident on the area normally.
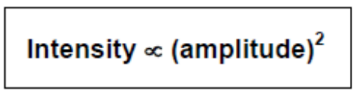
A sound wave of amplitude $0.20 \mathrm{~mm}$ has an intensity of $3.0 \mathrm{~W} \mathrm{~m} \mathrm{~m}^{-2}$.
What will be the intensity of a sound wave of the same frequency which has an amplitude of $0.40 \mathrm{~mm}$ ?
Solution:
The relation $\quad l \propto(\text { amplitude })^2$
can be expressed as
$I=k(\text { amplitude })^2$
where $k$ is the constant of proportionality.
Substituting
$
3.0 \mathrm{~W} \mathrm{~m}^{-2}=k(0.20 \mathrm{~mm})^2
$
New intensity,
$
I=k(0.40 \mathrm{~mm})^2
$
$
\frac{(2)}{(1)}: \quad \frac{I}{3.0 \mathrm{~W} \mathrm{~m}^{-2}}=4 \quad \rightarrow I=12.0 \mathrm{~W} \mathrm{~m}^{-2} \text {. }
$

Analyse and interpret graphical representations of
transverse and longitudinal waves.
- In a wave, there are two directions of motions:
- direction of propagation of energy (which is the direction of motion of the wave
- direction of oscillation of the particles in the wave.
A transverse wave is one in which the direction of propagation of energy is perpendicular to the direction of oscillation of the particles in the wave.
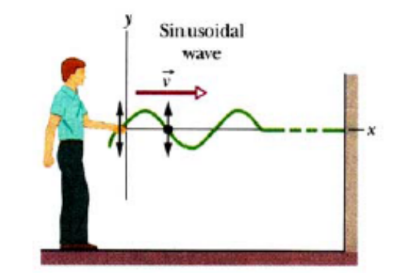
The string element’s motion is perpendicular to the wave’s direction of travel. This is a transverse wave.
In the example of a wave travelling along a string (or a wave travelling along a slinky diagrams above, the direction of propagation of the wave is along the string. If the wave is started from one end of the string by the oscillation of the first element in the direction perpendicular to the string, then this wave travelling along the string is an example of a transverse wave.
A longitudinal wave is one in which the direction of propagation of energy is parallel to the direction of oscillation of the particles in the wave.
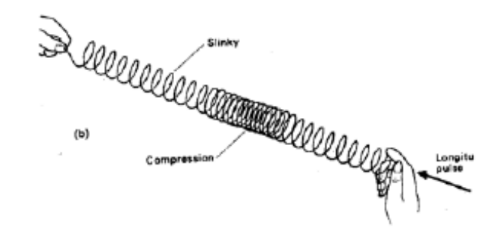
A visual demonstration of a longitudinal wave.
When a sound wave set up by the vibrating piston propagates along the pipe of air, the direction of propagation of sound energy is along the pipe to the right. The direction of oscillation of the air layers is back and forth, parallel to this direction. Hence sound wave is an example of a longitudinal wave,
Graphs representing waves
Graph 1: Displacement vs. Position graphs
These are plotted with displacement, $\boldsymbol{y}$, against distance or position, $\boldsymbol{x}$.
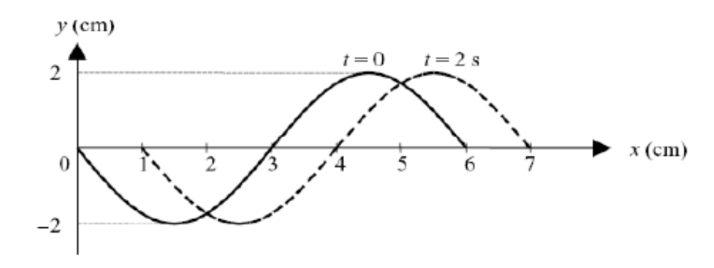
For a transverse wave moving from left to right along the $x$-axis, displacement of the particles in the wave, $y$, may be given a +ve sign for displacement upwards, and a -ve sign for displacement downwards. For a longitudinal wave moving from left to right along the $x$-axis, displacement of the particles in the wave, $y$, may be given a +ve sign for displacement to the right, and a -ve sign for displacement to the left.
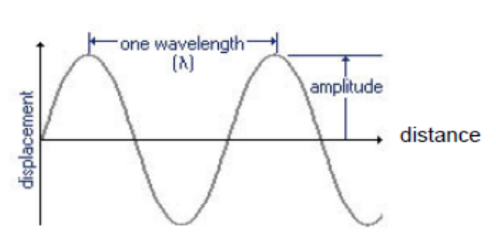
In Displacement vs. Position graphs,
- the graph represents the actual wave at an instant in time
- the distance between consecutive crests or consecutive troughs is one wavelength
- The maximum height of the vertical axis $=$ amplitude of wave
Graph 2: Displacement vs. Time graphs
In contrast, graphs used to represent an oscillation of a particle are plotted with displacement, $y$, against time, $\boldsymbol{t}$.
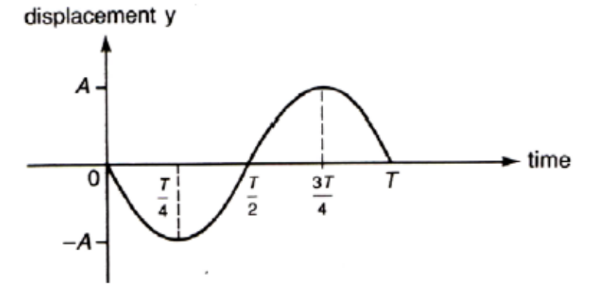
In the graph above, we are tracking the displacement of one particle only as time goes by. This does NOT represent the wave.
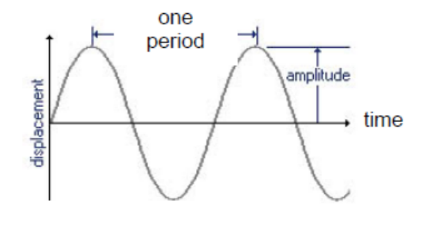
In Displacement vs. Time graphs,
- The graph represents the oscillation of one particle on the wave with time.
- the “distance” between consecutive crests or consecutive troughs is one period
- The maximum height of the vertical axis = amplitude of oscillation
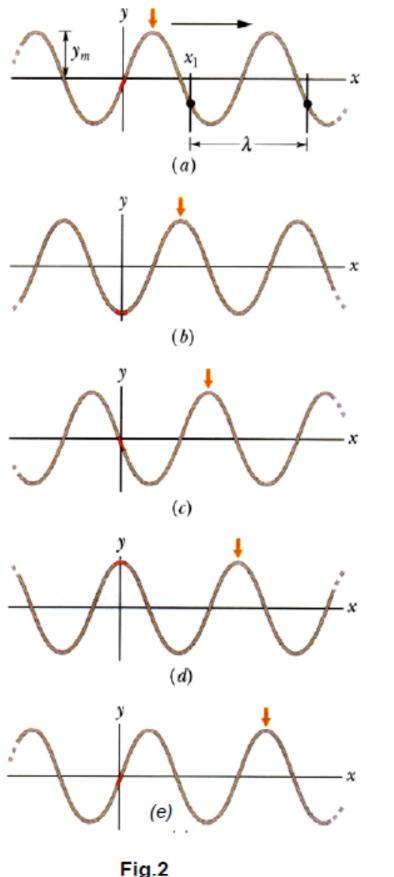
- Fig.2 shows 5 ‘snapshots’ of a transverse wave in a string, travelling in the +ve direction of an $x$-axis (left to right).
- The movement of the wave is indicated by the right-ward progress of the short down-pointing arrow, pointing at the middle ‘crest’ of the wave in snapshot (a).
- From snapshots (a) to (e), the short arrow moves to the right with the wave, but each particle in the string moves parallel to the $y$-axis (up and down). An example of such a particle is along the $y$-axis (shown darkened).
- Each snapshot is taken at an interval of $1 / 4$ period. One full oscillation takes place from (a) to (e).
Summary For Part (f):
(1) Displacement-time graph is for the oscillation of a particle in the wave.
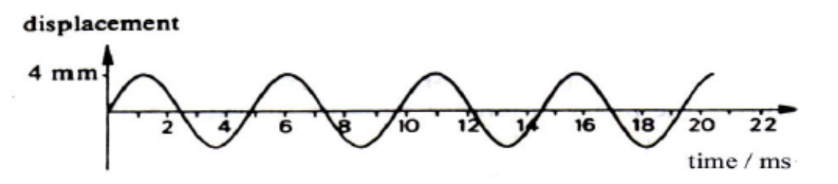
The graph above shows an element oscillating with an amplitude of $4 \mathrm{~mm}$. Its period of oscillation is about $5 \mathrm{~ms}$.
(2) Displacement-distance graph is for a snapshot of a wave motion at an instant.
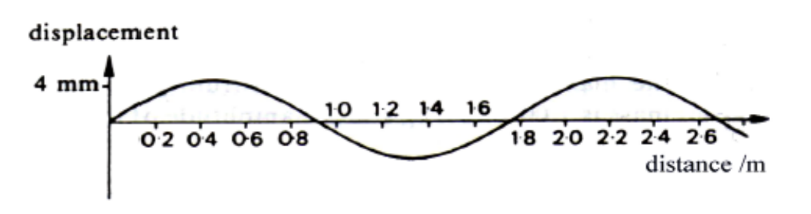
The graph above shows an instant of a wave with an amplitude of $4 \mathrm{~mm}$. Its wavelength is about $1.8 \mathrm{~m}$.
Example 7
The diagram below shows an instantaneous position of a string as a transverse progressive wave travels along it from left to right.

Which one of the following correctly shows the directions of the velocities of the points 1,2 and 3 on the strina?
Answer/Explanation
Solution
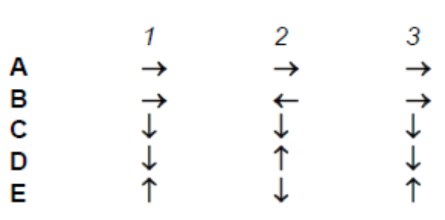
Knowing that the wave is traveling from LEFT to RIGHT, sketch how the wave would look like just an instant after:

Then look at the points concerned.
Since it is a TRANSVERSE wave, the particles only oscillates perpendicular to the wave direction.
This eliminates Answers A \& B.
Ans D
Example 8
The graph shows the shape at a particular instant of part of a transverse wave travelling along a string.
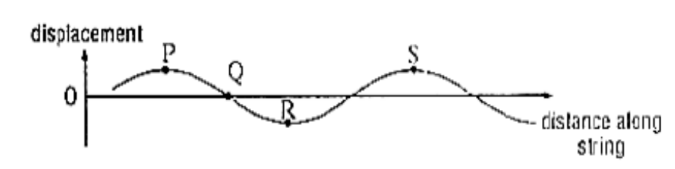
Which statement about the motion of elements of the string is correct?
A The speed of the element at $P$ is a maximum
B The displacement of the element at $\mathrm{Q}$ is always zero
C The energy of the element at $R$ is entirely kinetic
D The acceleration of the element at $\mathrm{S}$ is a maximum
Answer/Explanation
Solution:
Although the graph represents the whole wave at an instant in time, the question requires you to analyse the motion of the individual particles within the wave at this instant.
$\begin{array}{lll}\text { Element P: At extreme end of oscillation } & \rightarrow & \text { stationary } \\ \text { Element Q: At equilibrium position } & \rightarrow & \text { moving fastest } \\ \text { Element R: At extreme end of oscillation } & \rightarrow & \text { stationary, no kinetic energy } \\ \text { Element S: At extreme end of oscillation } & \rightarrow & \text { max displacement, max acceleration }\end{array}$
Ans: D
The frequency of sound using a calibrated CRO (This topic was done in Second chapter : Measurement & Techniques)
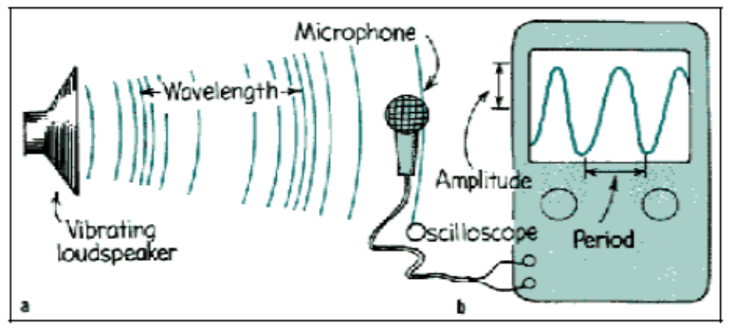
A calibrated c.r.o. (cathode-ray oscilloscope) implies that the time-base is set such that the period, $T$, of oscillations of the air layers detected by the microphone may be read.
Using the relation
$
f=\frac{1}{T}
$
the frequency, $f$, of sound produced by the vibrating loudspeaker may be determined.
Sample problem (This topic was done in Second chapter : Measurement & Techniques)
The trace shown appeared on an oscilloscope screen with the time-base set to $2.0 \mathrm{~ms}^{-1}$.
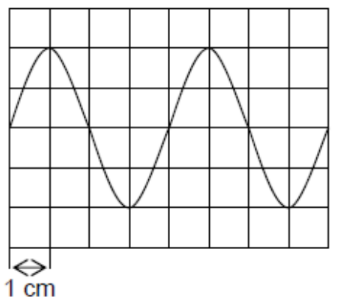
What is the frequency of the signal?
A $40 \mathrm{~Hz}$ B $125 \mathrm{~Hz}$ C $250 \mathrm{~Hz}$ D $500 \mathrm{~Hz}$
Answer/Explanation
Solution
Period, $T=2.0 \mathrm{~ms} \mathrm{~cm}^{-1} \times 4 \mathrm{~cm}=8.0 \mathrm{~ms}$
Frequency, $f=\frac{1}{T}=\frac{1}{8 \times 10^{-3} \mathrm{~s}}=125 \mathrm{~Hz}$
The wavelength of sound using stationary waves
• This topic would be studied in detail in next chapter ‘Superposition’.
• Please refer to notes on Stationary Waves in the topic Superposition.
