Polarization is a phenomenon associated with transverse waves
• Process by which a wave’s oscillations are made to occur in one plane only.
• Associated with transverse waves only.
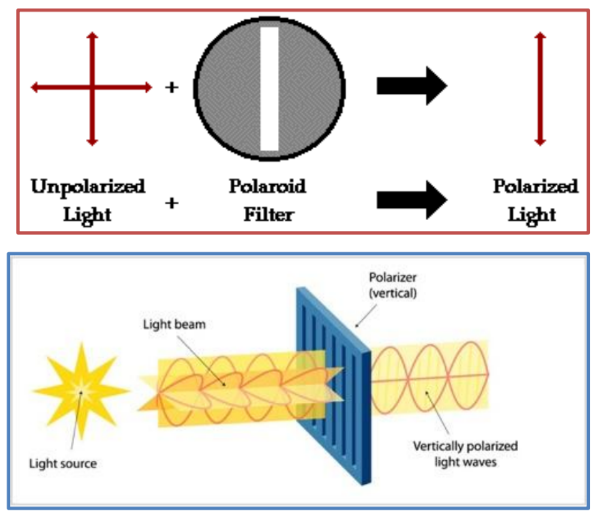
Note : Here, Polarization of light is analogous to that shown in the diagrams.
The Ficket Fence Analogy
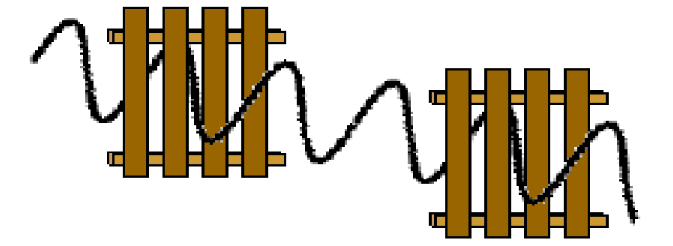
When the piclots of both fences ane aliged in the pertical dinection, a pertical whiration canmaloe it though both ferces.
Show an understanding that Polarisation is a phenomenon associated with transverse waves
Polarization by Use of a Polaroid Filter
• The most common method of polarization involves the use of a Polaroid filter.
• Polaroid filters are made of a special material that is capable of blocking one of the two planes of vibration of an electromagnetic wave.
• In this sense, a Polaroid serves as a device that filters out one-half of the vibrations upon transmission of the light through the filter. When unpolarized light is transmitted through a Polaroid filter, it emerges with one-half the intensity and with vibrations in a single plane; it emerges as polarized light.
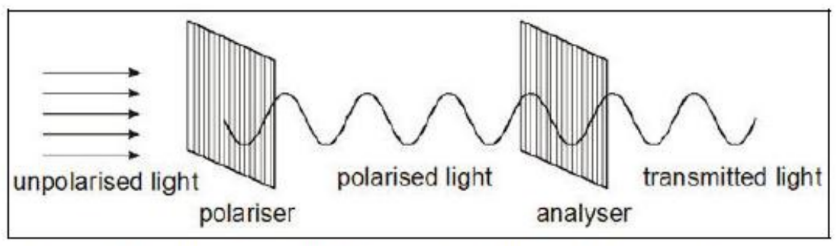
Light travelling parallel to polariser $\rightarrow$ the transmitted light has (almost) the same intensity as the polarised light (i.e. the amplitude of the light wave is identical).
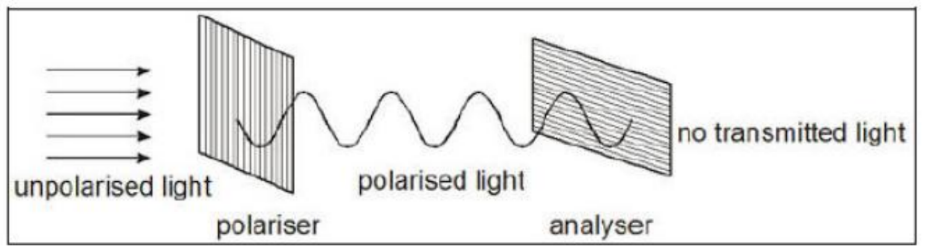
When the $2^{\text {nd }}$ polariser, or the Analyser is perpendicular to polariser, no transmitted light is observed. Hence, intensity is zero. (i.e. the amplitude of the light wave is zero).
A longitudinal waves cannot be Polarised. Why?
A longitudinal waves cannot be polarised because the particles in the wave oscillate parallel to the wave direction and cannot be restricted to vibrate in any plane.
Applications of Polarizations
(1) Polaroid sunglasses
– The glare from reflecting surfaces can be diminished with the use of Polaroid sunglasses.
– The polarization axes of the lens are vertical, as most glare reflects from horizontal surfaces.

Applications of Polarizations
2) Polarization is also used in the entertainment industry to produce and show 3-D movies.
HOW 3D WORKS (not in syllabus, just for your information only)
Three-dimensional movies are actually two movies being shown at the same time through two projectors.
The two movies are filmed from two slightly different camera locations. Each individual movie is then projected from different sides of the audience onto a metal screen.
The movies are projected through a polarizing filter. The polarizing filter used for the projector on the left may have its polarization axis aligned horizontally while the polarizing filter used for the projector on the right would have its polarization axis aligned vertically.
Consequently, there are two slightly different movies being projected onto a screen. Each movie is cast by light that is polarized with an orientation perpendicular to the other movie. The audience then wears glasses that have two Polaroid filters. Each filter has a different polarization axis – one is horizontal and the other is vertical. The result of this arrangement of projectors and filters is that the left eye sees the movie that is projected from the right projector while the right eye sees the movie that is projected from the left projector. This gives the viewer a perception of depth.
QUESTION TIME ! Check your understanding on Polarization
Question
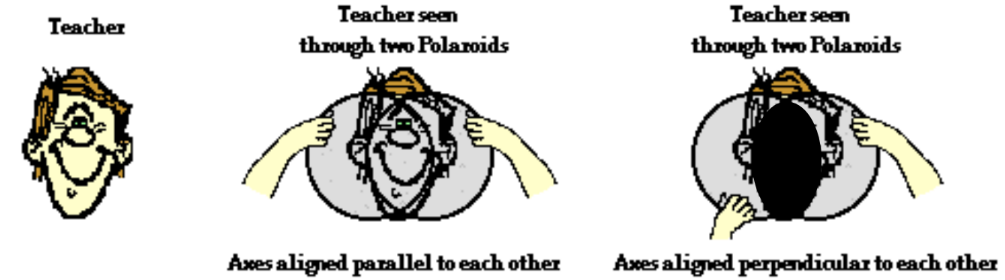
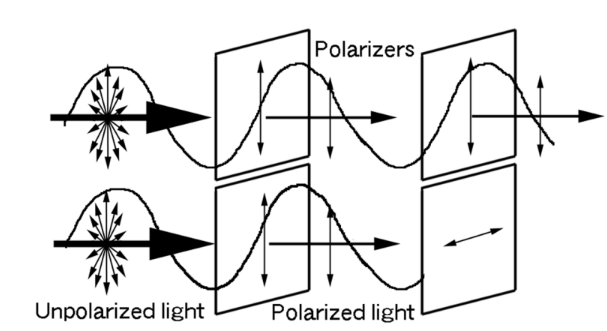
1. Suppose that light passes through two Polaroid filters whose polarization axes are parallel to each other. What would be the result?
Answer/Explanation
Answer
The first filter will polarize the light, blocking one-half of its vibrations. The second filter will have no affect on the light. Being aligned parallel to the first filter, the second filter will let the same light waves through.
Question
2. Which of the following cannot be polarised?
A-infrared waves
B-microwaves
C-sound waves
D- ultraviolet waves
Answer/Explanation
• Answer: C – Sound waves
A longitudinal waves cannot be polarised because the particles in the wave oscillate parallel to the wave direction and cannot be restricted to vibrate in any plane.
Question
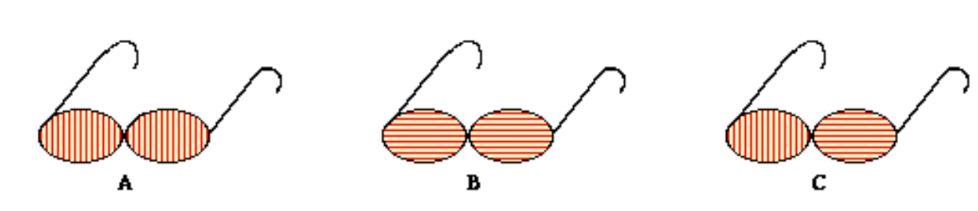
3. Consider the three pairs of sunglasses below. Identify the pair of glasses which is capable of eliminating the glare resulting from sunlight reflecting off the calm waters of a lake? _________ Explain.
(The polarization axes are shown by the lines.)
Answer/Explanation
Answer: A
• The glare is the result of a large concentration of light aligned parallel to the water surface. To block such plane-polarized light, a filter with a vertically aligned polarization axis must be used.

Figure 12.20: Polarising filters are used in photography – there is no glare and you can see the sharks and the boy snorkeling.
Malus’s law
Figure 12.21 shows plane polarised light incident at a Polaroid. The transmission axis of this Polaroid is at an angle θ to the plane of the incident light. Now you already know that when θ = 0, then the light will go through the Polaroid, and when θ = 90°, there is no transmitted light. The intensity of the transmitted light depends on the angle θ.
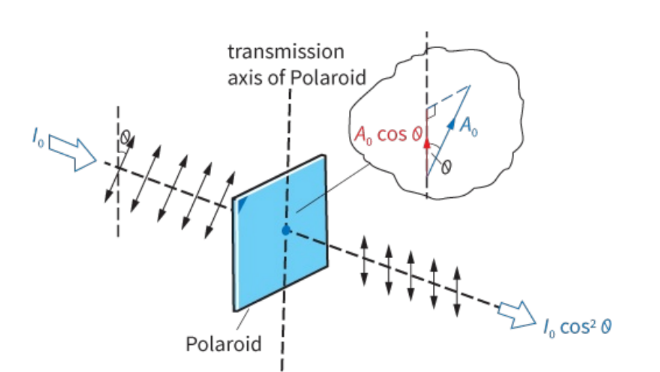
Figure 12.21: The amplitude, and hence the intensity of light, transmitted through the Polaroid depends on the angle θ.
Consider the incident plane polarised light of amplitude $A_0$. The component of the amplitude transmitted through the Polaroid along its transmission axis is $A_0 \cos \theta$. You know that the intensity of light is directly proportional to the amplitude squared. So, the intensity of light transmitted will be given by the expression:
$
I=I_0 \cos ^2 \theta
$
where $I_0$ is the intensity of the incident and $I$ is the transmitted intensity at an angle $\theta$ between the transmission axis of the Polaroid and the plane of the incident polarised wave.
The relationship is known as Malus’s law.

Note that the fraction of the light intensity transmitted is equal to $\cos ^2 \theta$. This means that a graph of $I$ against $\theta$ is a cosine squared graph, see Figure 12.22.
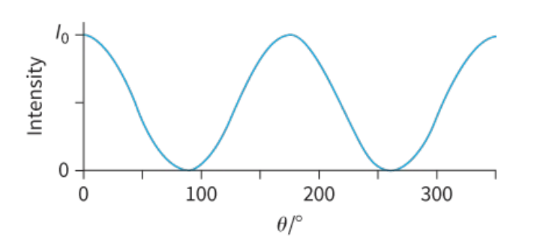
Figure 12.22: Variation of transmitted intensity $I$ with angle $\theta$. Notice maximum intensity when $\theta=0^{\circ}$, $180^{\circ}$ and so on, and zero when $\theta=90^{\circ}, 270^{\circ}$ and so on.
Questions
15 Explain what happens to unpolarised light incident at a Polaroid.
16 Plane polarised light of intensity $12 \mathrm{~W} \mathrm{~m}^{-2}$ is incident at a Polaroid.
Calculate the intensity of the transmitted light when the angle between the plane of polarisation of the incident light and the transmission axis of the Polaroid is
a $45^{\circ}$
b $60^{\circ}$.
17 Plane polarised light is incident at a Polaroid.
Calculate the angle $\theta$, which gives transmitted light of intensity $30 \%$ that of the incident intensity of light.
REFLECTION
Can you think of any applications of Malus’s law?
Make a list of some key words in this chapter. Ask a classmate to make a similar list. Now compare your
lists. How good was your list? Did you miss out anything important? What things might you want more
help with?
