Recap….
- Refer Ripple tank experiment
- Demonstration of Ripple tank experiment to show wave properties.
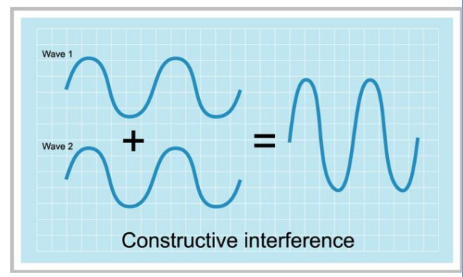
• Refer the figure on right with two waves arriving at a point at the same time in opposite directions.
• If they arrive in Phase – that is, if their crests arrive at exactly the same time – they will interfere constructively.
• A resultant wave will be produced which has crests much higher than either of the two individual waves and troughs which are much deeper.
• If the 2 incoming waves have the same frequency and equal amplitude A, the resultant wave produced by constructive interference has an amplitude of 2A.
• The frequency of the resultant is the same as that of incoming waves.
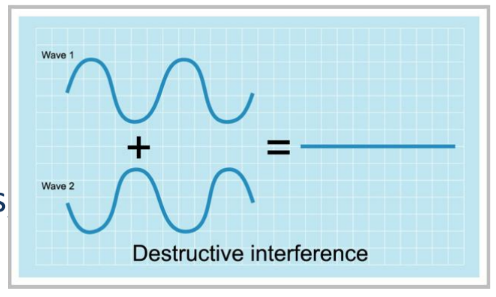
• Refer the figure on right with two waves arriving at a point at the same time.
• If they arrive out of Phase – that is, if the crests of one wave arrive at same time as the troughs from the other – they will interfere destructively.
• A resultant wave will have a smaller amplitude. (based on case to case)
• In the case shown in figure where the incoming waves have equal amplitude, the resultant wave has zero amplitude.
Interference and Superposition of Waves
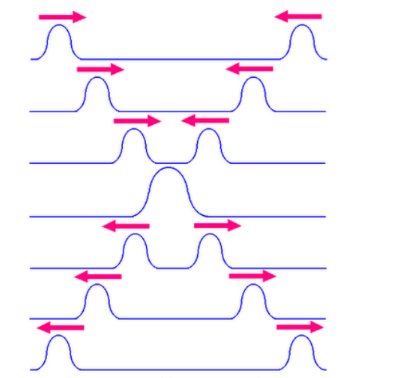
• When two waves meet they will interfere and superpose. After they have passed they return to their original forms. This is true if they are coherent or not.
• At the point they meet, the two waves will combine to give a resultant wave whose amplitude (or intensity) may be greater or less than the original two waves.
• The resultant displacement can be found by adding the two displacements together. This phenomenon leads to the Principle of Superposition.
The principle of Superposition
• The Principle of Superposition states that when two or more waves meet at a point, the resultant displacement at that point is equal to the sum of the displacements of the individual waves at that point.
Note : Displacement is a vector, so remember to add the individual displacements taking account of their directions.
Application of the Principle of Superposition
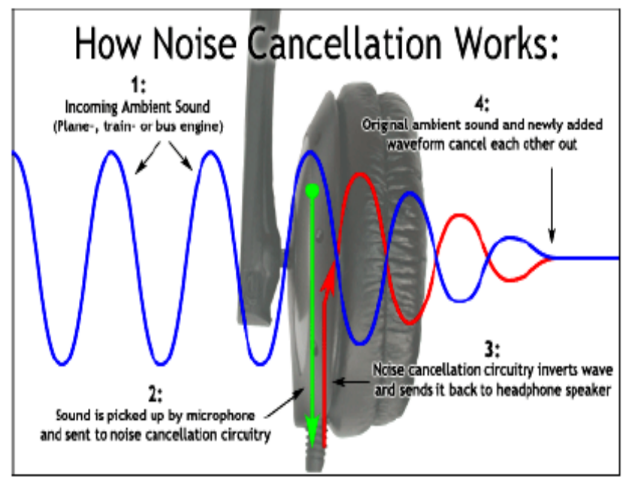
$\underline{\text { Active Noise Cancellation }}$
The muffling of ambient noise using insulating material in the headphones is called passive noise cancellation.
Active noise cancellation utilizes the principle of superposition to pick up the ambient noise, inverts the wave and generates this sound wave within the headphone. This inverted wave cancels the ambient noise, preserving only the sound waves that the listener wants to hear.
Note : The transverse shown in above figure is for the demo of cancellation of noise only. Remember, sound waves are to be represented in longitudinal form.
Stationary Wave
- A stationary wave is set up by the superposition of two progressive waves of the same type, amplitude and frequency travelling in opposite directions.
- A stationary (or standing) wave is one in which some points are permanently at rest (nodes), others between these nodes are vibrating with varying amplitude, and those points with the maximum amplitude (antinodes) are midway between the nodes.
This is not in Syllabus, this is included here for your understanding on stationary waves Melde’s apparatus to illustrate stationary waves in stretched string By adjusting the weight of the scale pan, stationary waves are set up as shown below.
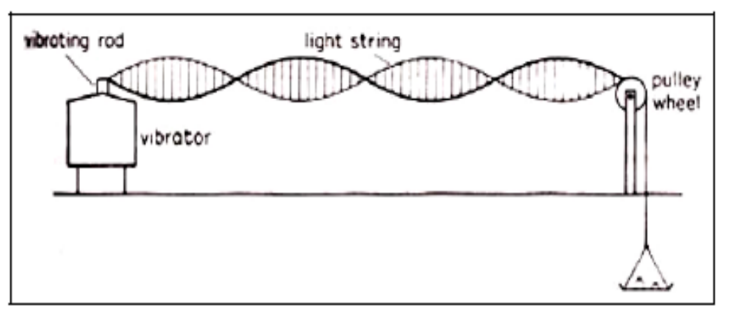
Uses and application of Melde’s experiment (for your information only)
- Melde’s experiment teaches us creation of standing waves.
- One can create a great product of neutralising the sounds by creating sounds with same wave length and frequency as the source.
- For example : If we know exactly the frequency of any machine ( say an aeroplane flying over your building every day during take off and landing) and if we can measure the wave length of sounds that machine creates..create a product that can create similar waves in opposite direction, so that they undergo mechanical interference and the machine sound is neutralised.
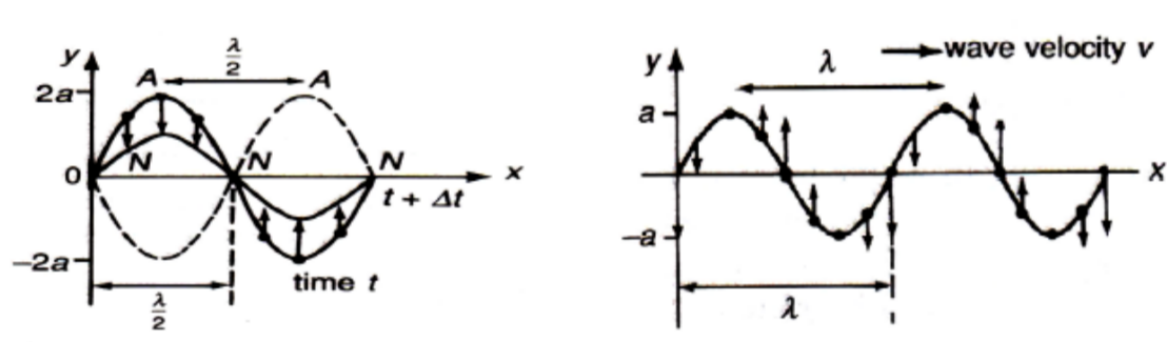
Characteristics of Stationary Waves
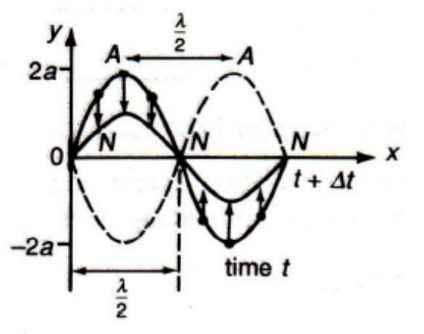
i. There is no sign of any progressive wave in either direction.
ii. Individual particles are oscillating with the same frequency, except at the nodes.
iii. The amplitudes of oscillation of the particles vary from a maximum at the antinodes $(A)$ to zero at the nodes $(\mathrm{N})$.
iv. All particles in the same segment or loop (region between 2 adjacent nodes) are vibrating in phase. Adjacent segments are anti-phase.
v. Adjacent nodes or adjacent antinodes are half a wavelength apart, i.e. $\mathrm{NN}=\mathrm{AA}=\frac{\lambda}{2}$
vi. A node and the next antinode are $\frac{\lambda}{4}$ apart.
vii. Energy is trapped (stored) in stationary waves, since there is no energy is transferring away.
Formation of Stationary Waves in Strings
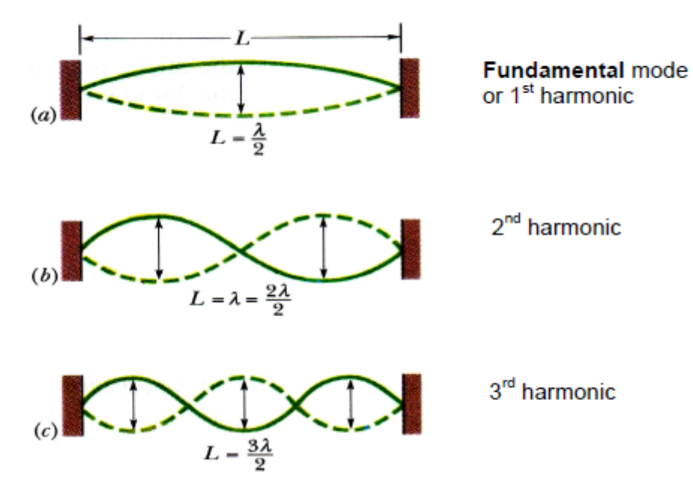
Let a string be stretched between two clamps separated by a fixed distance $L$.
When the string is plucked, struck or bowed, it can vibrate in several modes simultaneously.
The simplest possible pattern of the stationary wave consists of one loop (fundamental mode), with the nodes at the 2 ends of the string – diagram (a).
The next simplest pattern has 2 loops, and the next has 3 loops…etc.
In short, just add nodes between the 2 ends, for subsequent modes of vibration.
Formation of Stationary Sound Waves in air in Pipes
1. Stationary sound waves in air can be formed in both closed and open pipes.
2. In a closed pipe, when a sound wave is originated from the open end, the sound wave propagated into the pipe is reflected by the cylindrical wall and from the closed end. A stationary wave is then formed.
At resonance,
a) node $\mathrm{N}$ is always formed at the closed end of the pipe
– the air layer at this end is permanently at rest
b) antinode $A$ is formed at the open end of the pipe
– the air layer at this end is free to vibrate
3. In an open pipe, when a sound wave is originated from the open end, the sound wave propagated into the pipe to the other open end where it is reflected by the walls and on encountering air at the other open end. A stationary wave is set up.
At resonance, since the ends of the pipe are open, both ends are antinodes.
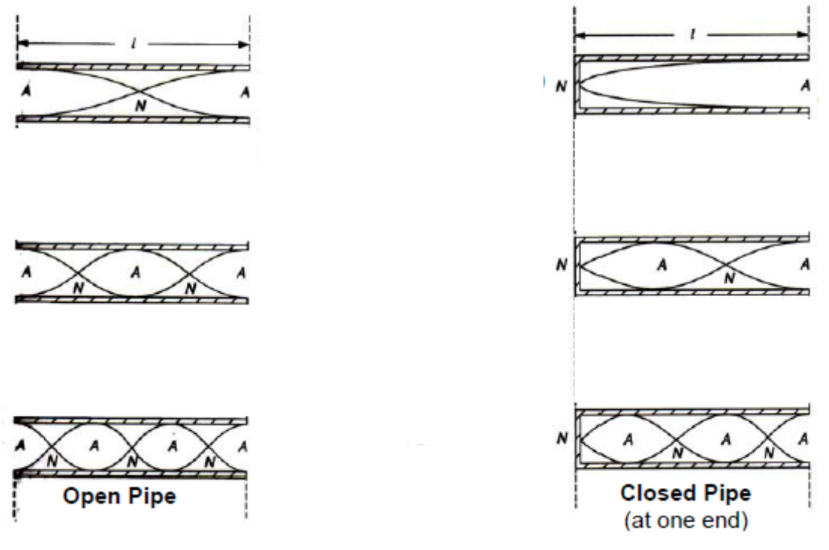
The resonance of sound in pipe may be varied by changing either the frequency of the sound wave, or length of the pipe.
Formation of Stationary Sound Waves in air
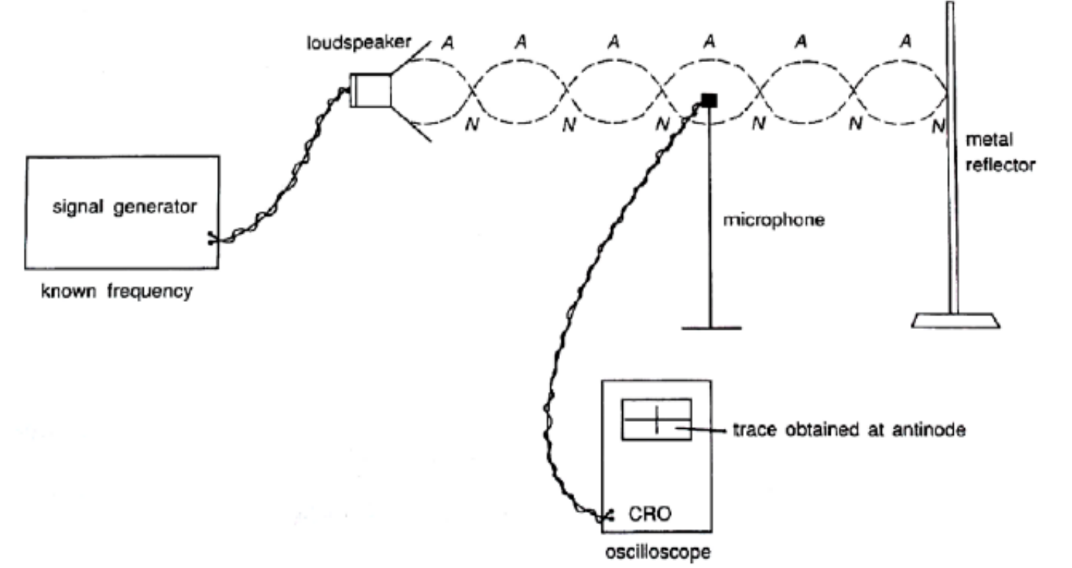
Stationary sound waves in air can be demonstrated using the set-up as shown above.
Note : In A level Physics syllabus, this part appears in previous chapter ‘waves’.
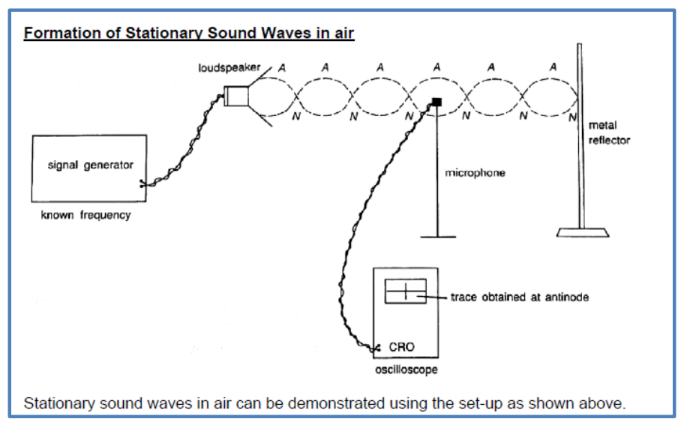
i. The incident sound wave is generated by the loudspeaker attached to a signal generator.
ii. The incident wave is reflected by the metal reflector (which must be appropriately positioned at a node). The reflected wave and the incident wave superpose to form a stationary wave.
iii. The detection of nodes and antinodes is done using a microphone attached to a CRO.
iv. By moving the microphone slowly forward and backward, the vertical trace (or amplitude) on the CRO screen is seen to vary from minimum to maximum, indicating the positions of nodes and antinodes.
[A] To measure the wavelength of the sound wave:
Measure the distance moved by the microphone, $d$, between 2 successive maxima or minima (e.g. $d=33 \mathrm{~cm})$.
Since this corresponds to $\frac{\lambda}{2}$, the wavelength $\lambda=2 d=2(33 \mathrm{~cm})=66 \mathrm{~cm}$
[B] To measure the frequency of the sound wave:
By measuring the period, $T$, of the sound wave, the frequency can be determined.
Set the time base of the CRO to a suitable value (e.g. $0.5 \mathrm{~ms} \mathrm{~cm}^{-1}$ ). Place the microphone where the CRO shows a sinusoidal trace. The period, $T$, is determined by measuring the distance between 2 crests or 2 troughs, $(e . \mathrm{g} .4 \mathrm{~cm})$.
$\therefore$ the period, $T=4 \mathrm{~cm} \times 0.5 \mathrm{~ms} \mathrm{~cm}^{-1}$
$
=2 \mathrm{~ms}=2 \times 10^{-3} \mathrm{~s}
$
Hence the frequency, $f=\frac{1}{T}=\frac{1}{2 \times 10^{-3}}=500 \mathrm{~Hz}$
[C] Hence, speed of sound can be calculated from $v=f \lambda=(500)\left(66 \times 10^{-2}\right)=330 \mathrm{~m} \mathrm{~s}^{-1}$
Sample problem 1
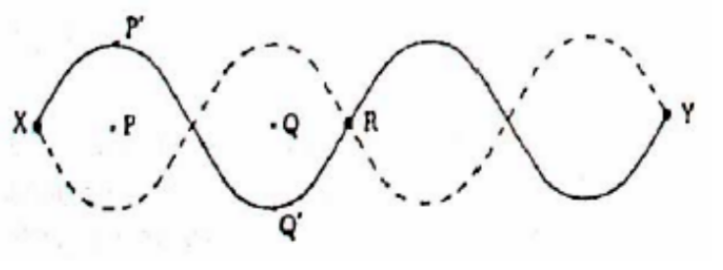
A string is stretched under constant tension between fixed points $X$ and $Y$. The solid line shows a stationary wave at an instant of greatest displacement. The broken line shows the other extreme displacement.
Which one of the following statements is correct?
A The distance between $\mathrm{P}$ and $\mathrm{Q}$ is one wavelength.
B A short time later, the string at $\mathrm{R}$ will be displaced.
C The string at $P^{\prime}$ and the string at Q’ will next move in opposite directions to one another.
D At the moment shown, the energy of the standing wave is all in the form of kinetic energy.
E The standing wave shown has the lowest possible frequency for this string stretched between $\mathrm{X}$ and $\mathrm{Y}$ under this tension.
Answer/Explanation
Solution:
A Incorrect. For a stationary wave, one wavelength contains two complete “loops” (i.e. distance $X R$ ). Hence, $P Q$ is only $1 / 2$ wavelength.
B Incorrect. $\mathrm{R}$ is a node, hence it will permanently be at rest.
C Correct ! In a stationary wave, particles in adjacent loops will always be moving opposite to each other (i.e. P’ will move down, and Q’ will move up).
D Incorrect. The energy is alternating between $\mathrm{KE}$ and $\mathrm{PE}$, depending on the location of each particle in the wave.
E Incorrect. The lowest possible frequency is the fundamental frequency, in which there will only be one “loop” between $X Y$.
(Ans: C)
Sample problem 2
A boy blows gently across the top of a piece of glass tubing the lower end of which is closed by his finger so that the tube gives its fundamental note of frequency, $f$. While blowing, he removes his finger from the lower end. The note he then hears will have a frequency of approximately
$\begin{array}{llllllllll}\text { A } & f / 4 & \text { B } & f / 2 & \text { C } & f & \text { D } & 2 f & \text { E } & 4 f\end{array}$
Answer/Explanation
Solution
At resonance, for a closed tube (with one end closed), the stationary wave (at fundamental frequency) formed is shown in (1). When the lower end is removed ( 2 open ends), the stationary wave (in fundamental mode) formed looks like (2).
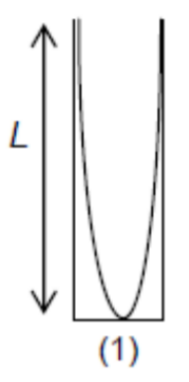
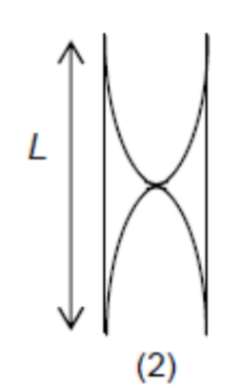
In (2): $L=1 / 2 \lambda \rightarrow \lambda=2 L$ If the frequency $=f_2$
Using $v=f \lambda \rightarrow f_2=\frac{v}{\lambda}=\frac{v}{2 L}=2 f$
$\ln (1): L=1 / 4 \lambda \rightarrow \lambda=4 L$ Given that the frequency $=f$
Using $v=f \lambda \rightarrow f=\frac{v}{\lambda}=\frac{v}{4 L}$
(Ans: D)
Sample problem 3
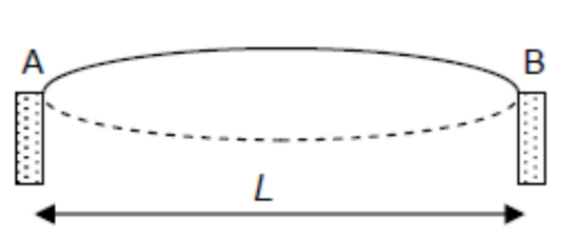
A suspension bridge is to be built across a valley where it is known that the wind can gust at $5 \mathrm{~s}$ intervals. It is estimated that the speed of transverse waves along the span of the bridge would be $400 \mathrm{~m} \mathrm{~s}^{-1}$.
The danger of resonant motions in the bridge at its fundamental frequency would be greatest if the span had a length of $\mathrm{m}$.
Answer/Explanation
Solution:
In fundamental mode, the stationary wave has a single “loop” at resonance, with nodes at the 2 ends.
Hence, if the length of the bridge, $L$, is equal to $1 / 2 \lambda$, the bridge will resonate with the fundamental frequency.
Given that the wind gusts at $5 \mathrm{~s}$ intervals $\rightarrow f_{\text {driver }}=\frac{1}{T}=\frac{1}{5}=0.2 \mathrm{~Hz}$
Using $v=f \lambda \rightarrow \lambda=\frac{v}{f}=\frac{400}{0.2}=2000 \mathrm{~m}$
Hence, the bridge has the danger of resonating (fundamental mode) if $L=1 / 2 \lambda=1000 \mathrm{~m}$
Sample problem 4
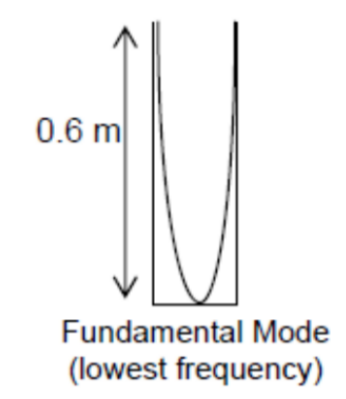
An organ pipe of effective length $0.6 \mathrm{~m}$ is closed at one end. Given that the speed of sound in air is $300 \mathrm{~m} \mathrm{~s}^{-1}$, the two lowest resonant frequencies are
Answer/Explanation
Solution:
For fundamental mode:
$
\begin{aligned}
& 1 / 4 \lambda=0.6 \mathrm{~m} \rightarrow \lambda=2.4 \mathrm{~m} \\
& f_{\text {fundamental }}=\frac{v}{\lambda}=\frac{300}{2.4}=125 \mathrm{~Hz}
\end{aligned}
$
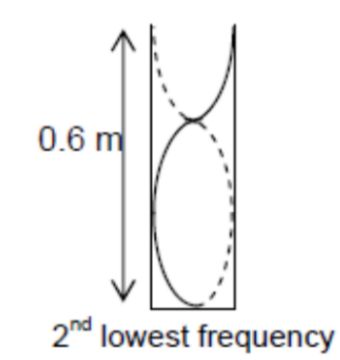
For $2^{\text {nd }}$ lowest frequency:
$
\begin{aligned}
& 3 / 4 \lambda=0.6 \mathrm{~m} \rightarrow \lambda=0.8 \mathrm{~m} \\
& f_{2 \text { nd lowest }}=\frac{V}{\lambda}=\frac{300}{0.8}=375 \mathrm{~Hz}
\end{aligned}
$
Hence the two lowest resonant frequencies are $125 \mathrm{~Hz} \& \underline{375 \mathrm{~Hz}}$.
Sample problem 5
A taut wire is clamped at two points $1.0 \mathrm{~m}$ apart. It is plucked near one end. What are the 3 longest wavelengths present on the vibrating wire?
Answer/Explanation
Solution
Step 1: Draw the 3 modes corresponding to the 3 longest wavelengths (between $X \& Y$ ).
Step 2: Since the wire is clamped at the 2 points ( $X \& Y)$, they must be nodes.

Step 3: Relate the length of wire to the corresponding wavelength, $\lambda$, in each case.
$\begin{aligned} & 1 / 2 \lambda=1.0 \mathrm{~m} \\ & \rightarrow \lambda=\underline{2.0 \mathrm{~m}}\end{aligned}$
$\lambda=\underline{1.0 \mathrm{~m}}$
$\begin{aligned} & (1.5) \lambda=1.0 \mathrm{~m} \\ & \rightarrow \lambda=\underline{0.67 \mathrm{~m}}\end{aligned}$
The formation of a stationary wave using a graphical method Nodes and Antinodes
Formation of a stationary (standing) wave
A stationary wave is formed when two progressive waves of the same type, wavelength and amplitude travel in opposite directions superpose in the same medium.
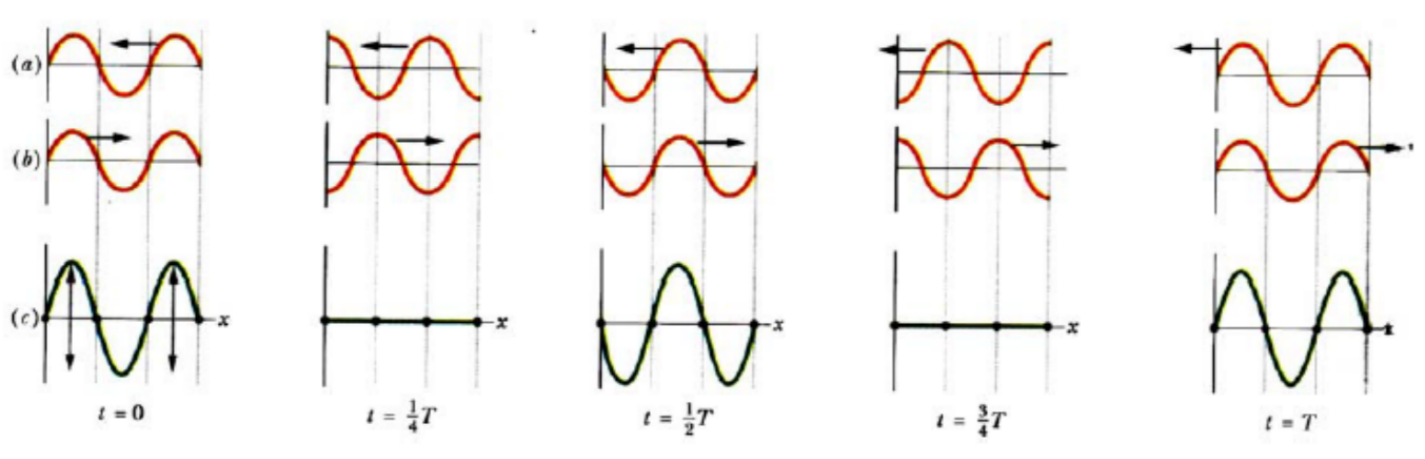
In the diagrams above, of the two progressive waves in a string, one is travelling to the left (a), and the other to the right (b).
The resultant wave (c) is a stationary wave, obtained by applying the superposition principle.
Note:
a) there are positions along the string which do not move – called nodes (marked by dots)
b) halfway between successive nodes are antinodes, where the amplitude of the resultant wave is maximum (double the amplitude of the individual waves).
c) wave patterns shown in diagram (c) are those of a stationary or standing wave because the wave patterns do not move left or right (i.e. the positions of the nodes and antinodes do not change).
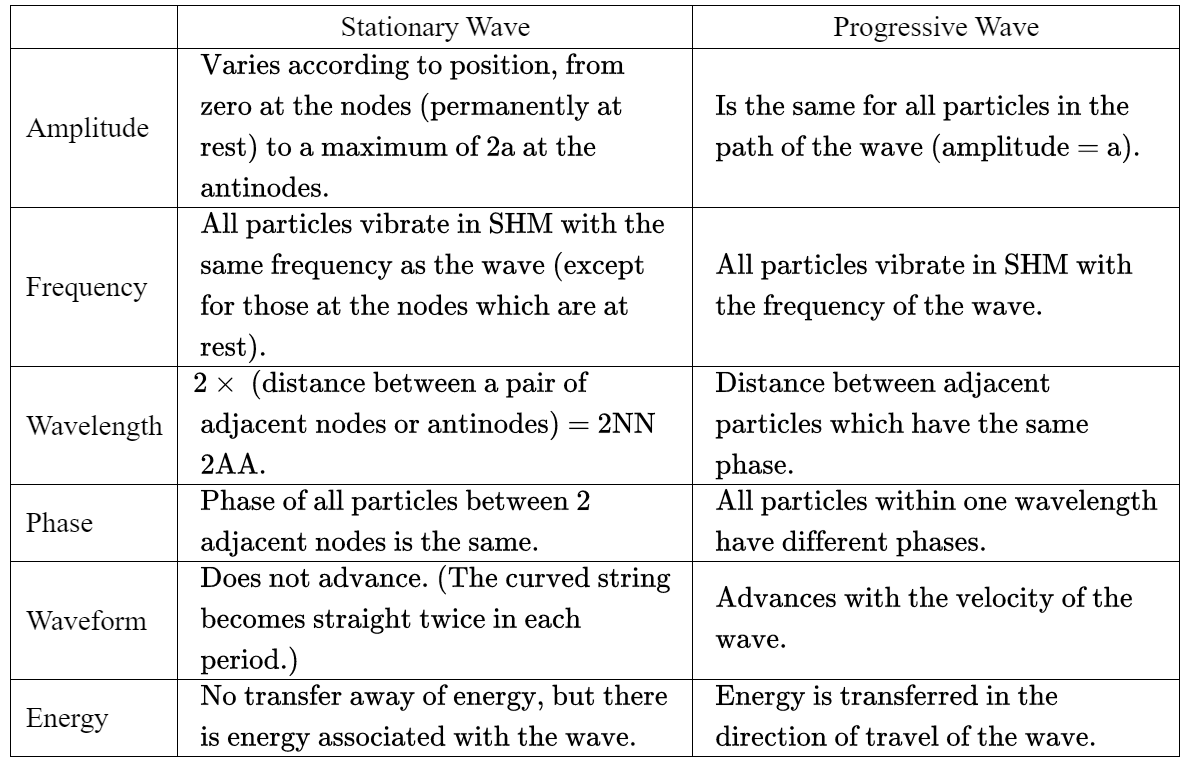
Comparison between Stationary and Progressive Wave Motions
Sample problem 6
A standing wave is set up on a stretched string $X Y$ as shown in the diagram. At which point(s) will be oscillation be exactly in phase with that at point $\mathbf{P}$ ?

Answer/Explanation
Solution:
In a stationary wave, all points between 2 successive nodes are in phase. In this case, 1 \& 2 are in phase with each other, but are in anti-phase with $\mathrm{P}$. Hence, only 3 is in phase with $P$.
