Interference
- Interference is the superposing of two or more waves to give a resultant wave whose displacement is given by the Principle of Superposition.
- Watch Demo (Name is Double slit coherent wave interference patterns)

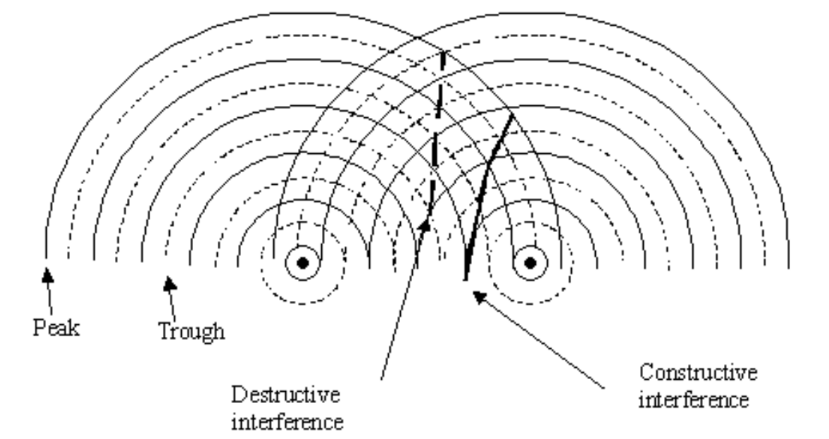
- At regions of maxima, constructive interference occurs (i.e. the waves arrive at these points in phase), resulting in maxima amplitude, hence high intensity.
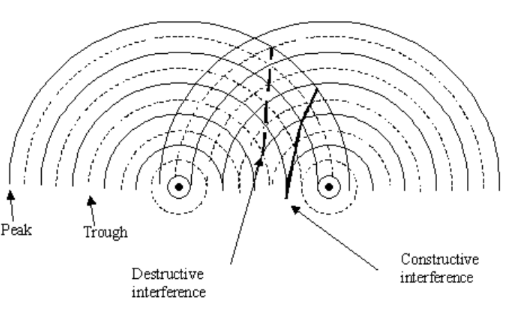
• At regions of minima, destructive interference occurs (i.e. the waves arrive at these points in anti-phase), resulting in minima or zero amplitude, hence low or zero intensity.
Experiments that demonstrate Two-source Interference
Thomas Young’s Double Slit Experiment
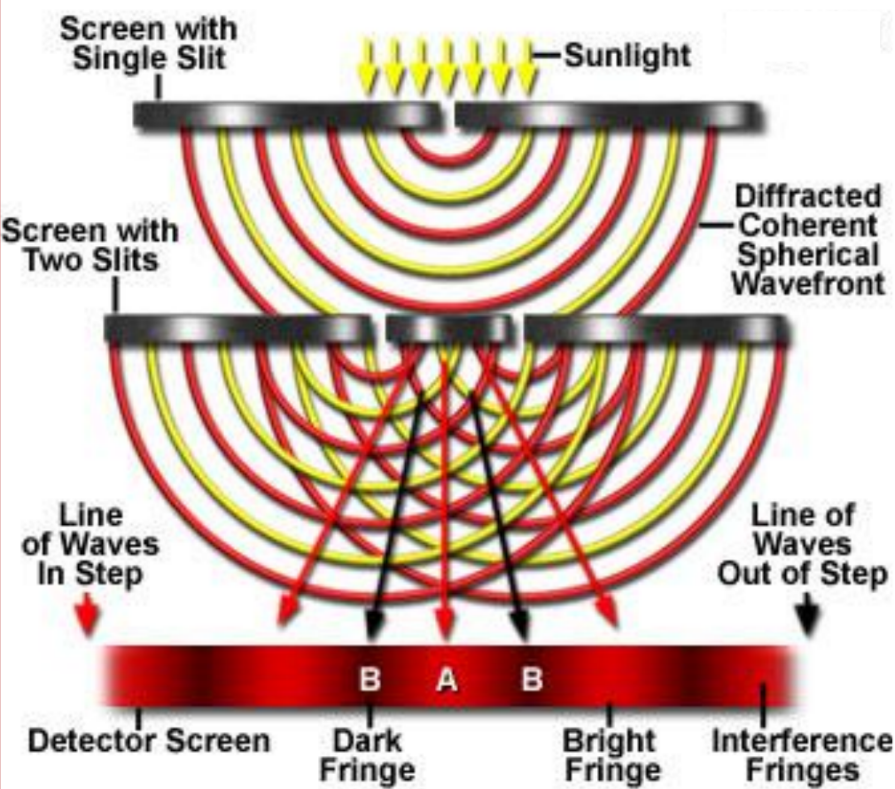
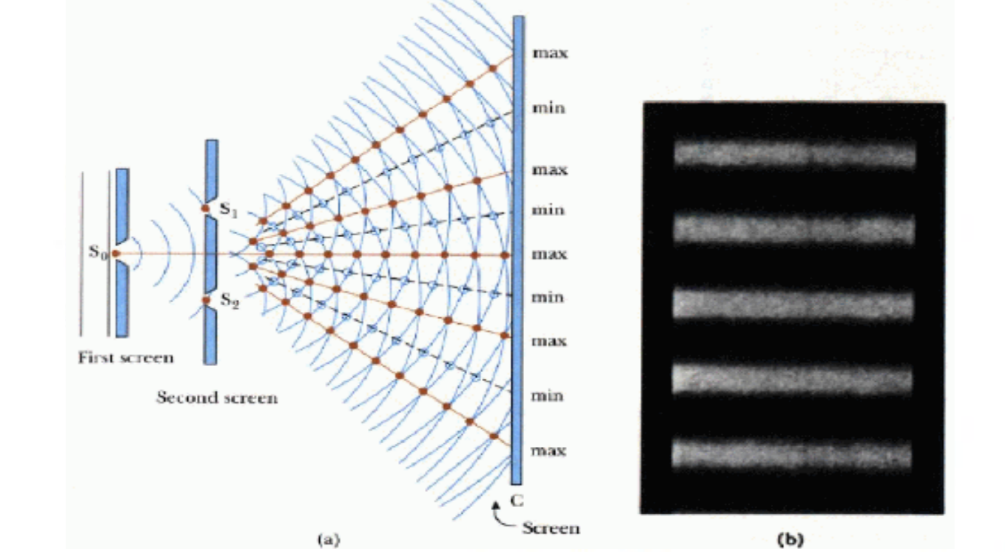
In diagram (a) above, the narrow double slits act as wave sources. Slit $S_1$ and $S_2$ behave as coherent sources (waves coming from them are always at a constant phase difference) that produce an interference pattern on screen $\mathrm{C}$.
This interference pattern (fringe pattern) is shown in diagram (b). Separation between successive bright fringes (centre to centre) is the fringe spacing.
The bright fringes are formed due to constructive interference (i.e. the waves arrive at these points in phase), while the dark fringes are due to destructive interference (i.e. the waves arrive at these points in anti-phase – hence no resultant amplitude, which then appears dark).
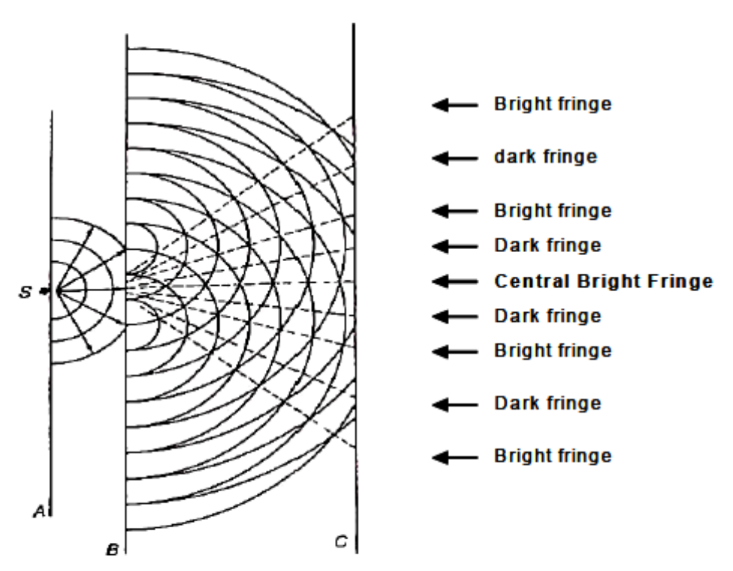
Schematic diagram of Young’s double-slit experiment is shown above.
Two-source interference with water
An interference pattern involving water waves is produced by two vibrating sources at the water surface. The lines represent crests, and the spaces between the lines represent troughs. The regions where the lines intersect (spaces also intersect) have constructive interference. The regions where lines intersecting spaces have destructive interference.
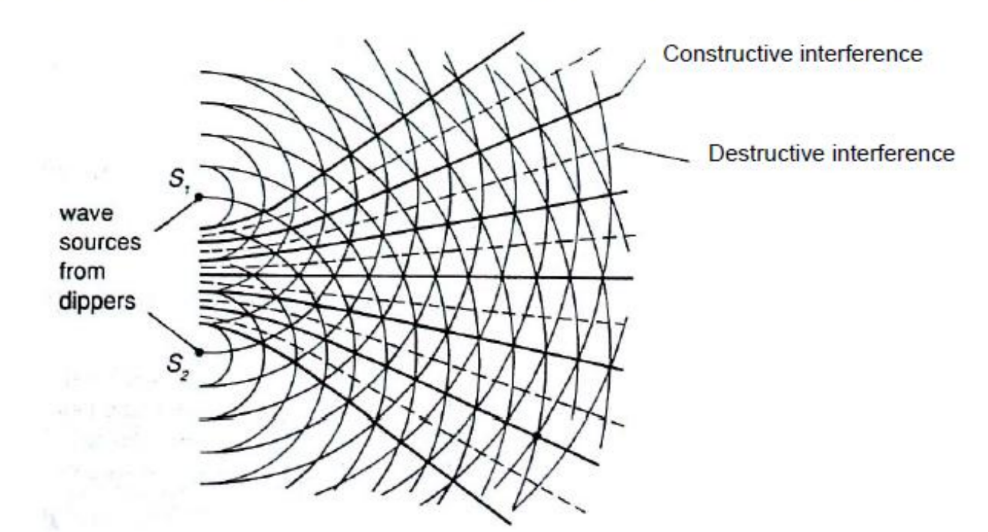
Conditions required for two-source interference fringes to be observed
For interference fringes to be observable:
- The sources must be coherent; that is, they must maintain a constant phase difference.
- The sources must have the same frequency (for light waves, this means that they must be monochromatic).
- The principle of superposition must apply (the sources must produce the same type of waves).
- The sources must have (approximately) the same amplitude.
For light waves,
* the wavelengths used should be in the visible range (400 $\mathrm{nm}$ to $700 \mathrm{~nm}$ ).
* the source (slit) separation $(d)$ is around the order of $10^{-4} \mathrm{~m}$.
* the screen-slits distance $D$ is around $1-2 \mathrm{~m}$.
Just for your understanding only: (not in syllabus)
What is the meaning of ‘a constant phase difference’ between two coherent waves’ ?
- The primary source of light is transition of electrons. This happens for every source be it the fluorescent tubes or the sun .
- As an electron jumps to its higher level it reaches an unstable excited state. It stays there for about
$10 \mathrm{~ns}$ and comes back to the ground state. Thus every 10ns a new stream of light is produced. - If we have two sources of light then the phase difference between any two waves would be random. In fact it would change every $10 n$ or so. This is why we don’t find interference in practical life.
- To have a constant phase difference between two waves (i.e. to be coherent.) the waves should be from a common source, so that there is no ab-nitio phase difference to get a constant phase difference and two waves (from the same source) can be made to have some path difference.
Conditions for constructive interference
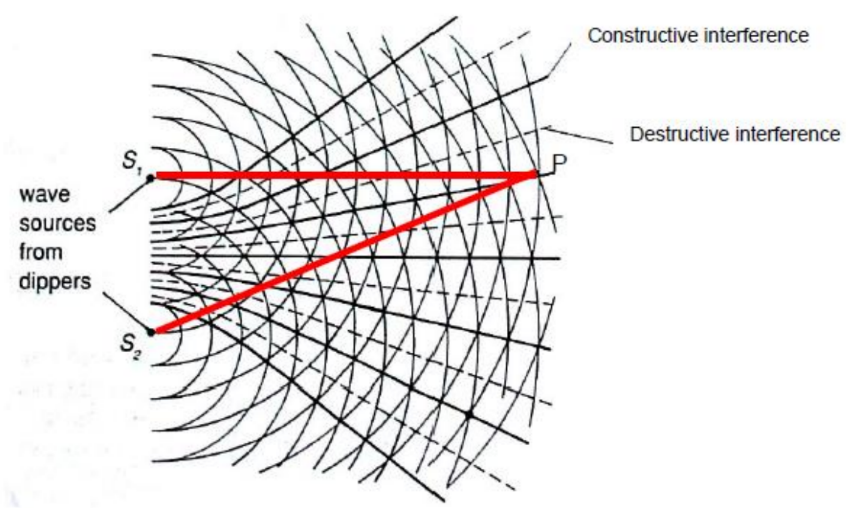
The 2 thick lines intersecting at $P$ represent the paths of water waves from the 2 sources to produce a constructive interference at $P$.
Length $S_2 P=14 \lambda$, length $S_1 P=13 \lambda \rightarrow$ their path difference $=14 \lambda-13 \lambda=\lambda$
For other points with constructive interference, the path difference must be $\boldsymbol{n} \boldsymbol{\lambda}$, where $n$ is an integer. The assumption here is that the source are in phase.
Conditions for destructive interference
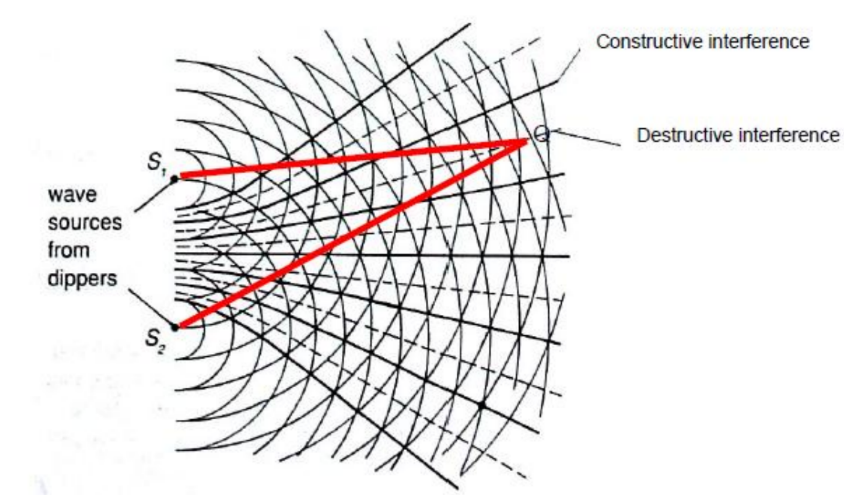
The 2 thick lines intersecting at Q represent the paths of water waves from the 2 sources to produce a destructive interference at $Q$.
Length $\mathrm{S}_2 \mathrm{Q}=14 \lambda$, length $\mathrm{S}_1 \mathrm{Q}=12 \frac{1}{2} \lambda \rightarrow$ their path difference $=14 \lambda-12 \frac{1}{2} \lambda=1 \frac{1}{2} \lambda$
For other points with destructive interference, the path difference must be $\left(n+\frac{1}{2}\right) \lambda$, where $n$ is an integer. The assumption here is that the source are in phase.
Using the equation $\lambda=\frac{a x}{D}$ for double-slit interference using light
Note : As per syllabus, you need to have an you don’t have to prove/derive the equation.
Young’s Double Slit
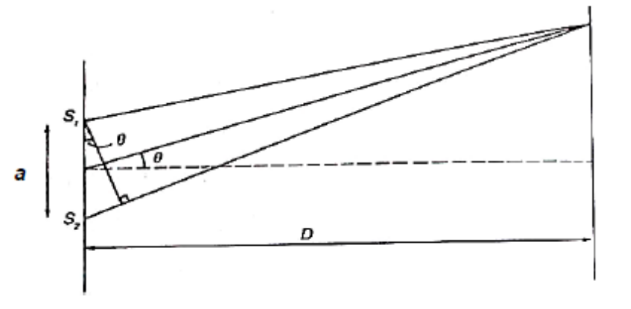
In the double slit experiment, bright \& dark fringes alternate at equal separation.
The double slit interference is given by the equation
$
\frac{\lambda}{a}=\frac{x}{D}
$
$\lambda$ is the wavelength of the light
$a$ is the separation of the slits
$\boldsymbol{x}$ is the separation of the fringes on the screen (fringe spacing, separation between centres of bright fringes, or centres of dark fringes)
$D$ is the separation between the screen and the double-slit
Check your understanding!
- Do headlights from a car form interference patterns? Why?
The interference would be ‘visible’ if the two sources are oscillating in phase or have a constant phase difference. This is why a single light source (as in young’s double slit experiment) is split to produce two which are then coherent. - In addition the separation of the headlamps is so large that any interference fringes would be too close together to be easily measurable, and the path difference between waves would render them no longer coherent.
- Note that, because the wavelength of light is so small (of the order of $10^{-7} \mathrm{~m}$ ) to produce observable fringes ‘ $D$ ‘ needs to be large and ‘a’ as small as possible. (This is one of the application of equation of young’s double slit experiment)
Sample problem 7
Which of the following statements must be true about two wave-trains of monochromatic light arriving at a point on a screen if the wave-trains are coherent?
A They are in phase.
B They have a constant phase difference.
C They have both travelled paths of equal length.
D They have approximately equal amplitudes.
E They interfere constructively.
Answer/Explanation
Solution (Ans: B)
Only $[B]$ is true as this is the meaning of coherence.
Sample problem 8
When a two-slit arrangement was set up to produce interference fringes on a screen using a monochromatic source of green light, the fringes were found to be too close together for convenient observation.
In which of the following ways would it be possible to increase the separation of the fringes?
A Decrease the distance between the screen and the slits.
B Increase the distance between the source and the slits.
C Have a larger distance between the two slits.
D Increase the width of each slit.
E Replace the light source with a monochromatic source of red light
Answer/Explanation
Solution: (Ans: E)
Since it is a double slit setup, using the equation $\frac{\lambda}{a}=\frac{x}{D} \rightarrow x=\frac{\lambda D}{a}$
A decrease $D \rightarrow x$ will decrease
B increase distance between source \& slits does not affect the fringe separation
C increase $a \rightarrow x$ will decrease
D increasing the width of the slit will not affect $x$, but will allow more light through, hence a brighter pattern
$\mathrm{E} \quad$ replace green light with red light. $\lambda_{\text {red }}>\lambda_{\text {green }} \rightarrow$ if $\lambda$ increases, $x$ will increases.
Sample problem 9
- Calculate the observed fringe width for a young’s double slit experiment using light of wavelength $600 \mathrm{~nm}$ and slits $0.50 \mathrm{~nm}$ apart. The distance from the slits to the screen is $0.80 \mathrm{~m}$.
Answer/Explanation
Solution :
Using $\lambda=\frac{a x}{D}$
$
\begin{aligned}
x & =600 \times 10^{-9} \times 0.80 / 0.50 \times 10^{-9} \\
& =960 \mathrm{~m}
\end{aligned}
$
