Use of a diffraction grating to determine the wavelength of light
• A diffraction grating is a plate on which there is a very large number of identical, parallel, very closely spaced slits.
• If a monochromatic light is incident on this plate, a pattern of narrow bright fringes is produced.
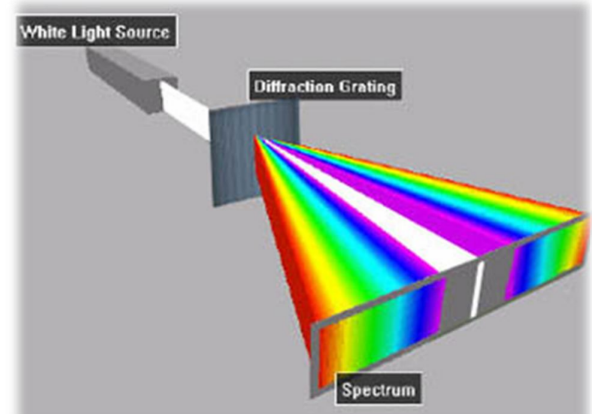
How a Diffraction Grating Works
When you look at a diffracted light you see:
– the light straight ahead as if the grating were transparent.
– a “central bright spot”.
– the interference of all other light waves from many different grooves produces a scattered pattern called a spectrum.
Application of Diffraction Grating
• A diffraction grating can be used to make a spectrometer and a spectrometer is a device that measures the wavelength of light.
The equation : $d \sin \theta=n \lambda$
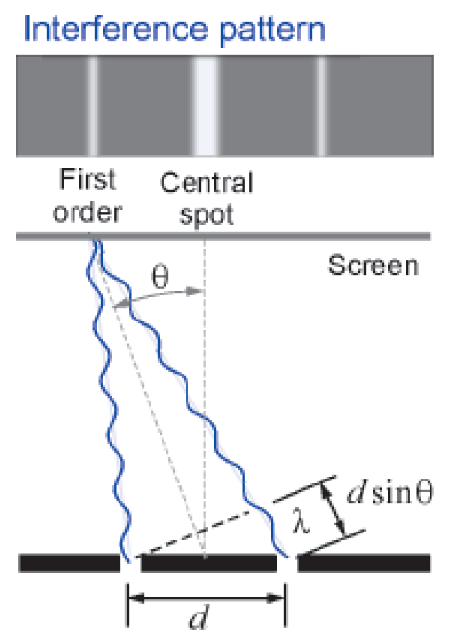
Figure 8.54 shows a parallel beam of light incident normally on a diffraction grating in which the spacing between adjacent slits is $d$. Consider first rays 1 and 2 which are incident on adjacent slits. The path difference between these rays when they emerge at an angle $\theta$ is $d \sin \theta$. To obtain constructive interference in this direction from these two rays, the condition is that the path difference should be an integral number. of wavelengths. The path difference between rays 2 and 3 , 3 and 4 , and so on, will also be $d \sin \theta$. The condition for constructive interference is the same. Thus, the condition for a maximum of intensity at angle $\theta$ is
$
d \sin \theta=n \lambda
$
where $\lambda$ is the wavelength of the monochromatic light used, and $n$ is a whole number.
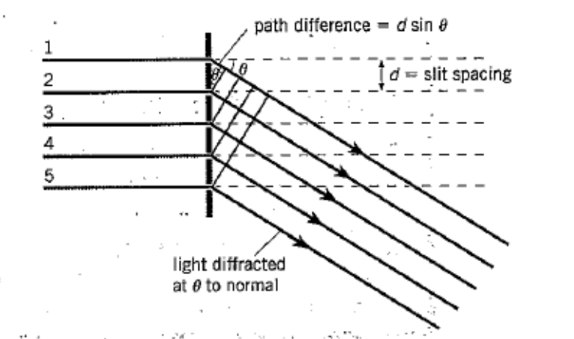
When $n=0, \sin \theta=0$ and $\theta$ is also zero; this gives the straight-on direction, or what is called the zero-order maximum. When $n=1$, we have the first-order diffraction maximum, and so on (Figure 8.55 ).
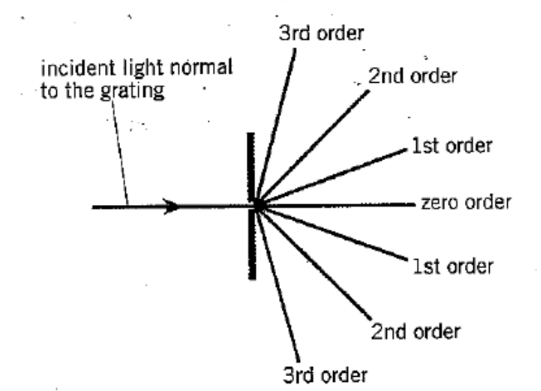
Figure 8.55 Maxima in the diffraction pattern of a diffraction grating
Sample problem 10
Monochromatic light is incident normally on a grating with $7.00 \times 10^5$ lines per metre. A second-order maximum is observed at an angle of diffraction of $40.0^{\circ}$. Calculate the wavelength of the incident light.
Answer/Explanation
The slits on a diffraction grating are created by drawing parallel lines on the surface of the plate: The relationship between the slit spacing $d$ and the number $N$ of lines per metre is $d=1 / N$. For this grating, $d=1 / 7.00 \times 10^5=1.43 \times 10^{-6} \mathrm{~m}$. Using $n \lambda=d \sin \theta$, $\lambda=(d / n) \sin \theta=\left(1.43 \times 10^{-6} / 2\right) \sin 40.0^{\circ}=460 \mathrm{~mm}$.
