Potential difference and Volt
- Defining p.d in terms of energy:
- $\Delta$ The potential difference between two points in a circuit is defined as the electrical energy converted to other forms of energy per unit charge passing between the two points.
- Alternatively, defining p.d in terms of power:
- $\Rightarrow$ The p.d. between two points in a circuit is defined as the rate of conversion of electrical energy to other forms of energy per unit current flowing between the two points.
In terms of energy:
$
\begin{aligned}
& \text { potential difference (p.d.) }=\frac{\text { energy converted }}{\text { charge }} \\
& \text { hence } V=\frac{W}{Q} \text { or } W=Q V .
\end{aligned}
$
In terms of power:
$
\begin{aligned}
& \text { potential difference (p.d.) }=\frac{\text { power converted }}{\text { current }} \\
& \text { hence } V=\frac{P}{l} \text { or } P=V \boldsymbol{I} .
\end{aligned}
$
where $V$ is the p.d., in volts $(V)$
$W$ is the energy converted, in joules $(\mathrm{J})$
$Q$ is the electric charge moved, in coulombs (C)
$P$ is the power converted, in watts $(W)$
$I$ is the electric current flowing, in amperes (A)
Since $V=I R$ from learning outcome (h), $P=I^2 R$.
From $V=\frac{W}{Q}, 1 \mathrm{~V}=1 \mathrm{~J} \mathrm{C}^{-1}$ defines the volt (in terms of energy).
The volt is the potential difference between two points in a circuit if one joule of electrical energy is converted to other forms of energy when one coulomb of charge passes between the two points.
Alternatively, from $P=\mathrm{VI}, 1 \mathrm{~V}=1 \mathrm{~W} \mathrm{~A}^{-1}$ defines the volt (in terms of power).
The volt is the potential difference between two points in a circuit if one watt of electrical power is converted to other forms of power when one ampere of current passes between the two points.
Note:
- Since the unit for p.d. is volt, p.d. is frequently called voltage.
- The p.d. can only be used if the two points are stated clearly. For a single circuit component, the two points are usually the two ends of the component hence the p.d. across the component.
- Sometimes the term “potential at a point” in a circuit is used. This has meaning only if there is a defined reference point for zero potential e.g. the electrical earth has zero potential.
Just for your info: The real Earth is electrically neutral. This means that it has the same number of electrons and protons, so their charges cancel out overall. Scientifically, we describe this by saying that the Earth has an Electric Potential of zero.
Solve problems using $\mathrm{V}=\frac{W}{Q}$
Example 4
An immersion heater is rated at $3000 \mathrm{~W}$ and is switched on for $2000 \mathrm{~s}$. During this time a charge of $25 \mathrm{kC}$ is supplied to the heater. Determine the potential difference across the heater.
Answer/Explanation
Solution:
$
V=\frac{W}{Q}=\frac{(3000)(2000)}{25000}=240 \mathrm{~V}
$
Sketch and explain the $I-V$ characteristics of a metallic conductor at constant temperature, a semiconductor diode and a filament lamp.
Sketch and explain the I-V characteristics of a metallic conductor at constant temperature
1) Metallic conductor at constant temperature
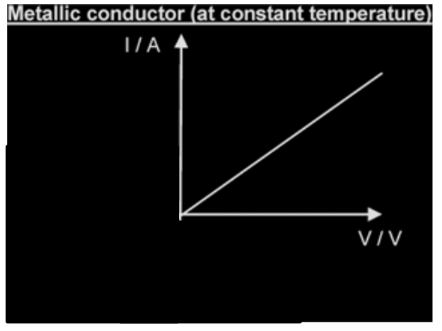
- The $I-V$ characteristic of a metallic conductor at constant temperature is a straight line through the origin. This implies constant $I-V$ ratio, i.e. constant resistance. Therefore a metallic conductor at constant temperature is an ohmic conductor.
- In terms of the movement of charge carriers, resistance in metallic conductors arises from the reduction in the drift velocity of free electrons due to collision with lattice ions. If the temperature of the conductor is kept constant, the lattice ion vibrations will remain the same hence its resistance will remain the constant.
- In short, the resistance of a metallic conductor is constant at constant temperature (ohmic conductor).
Sketch and explain the I-V characteristics of a semiconductor diode
(2) Semiconductor diode
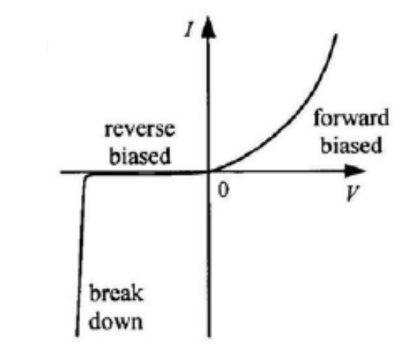
- A diode is a device that has a low resistance in one direction (forward-biased direction) and a very high resistance in the other direction (reverse-biased direction).
- The I-V characteristic of a forward-biased semiconductor diode is similar to that of a thermistor, i.e. resistance decreases as p.d. increases.
- The I-V characteristic of a reverse-biased semiconductor diode is nearly zero. If reverse-biased p.d. is too high, the diode will break down and conduct electricity.
(3) Filament lamp
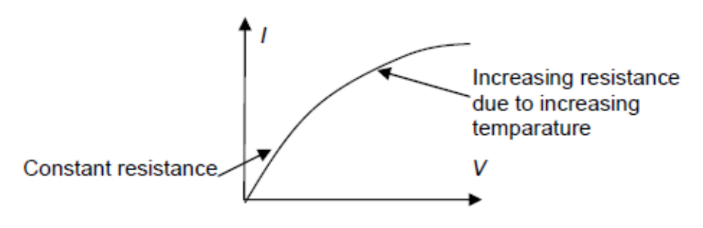
- A filament lamp contains a long thin wire made of metal with high melting point (e.g. tungsten).
- With low p.d. across the filament lamp, low current flowing through it and the heating effect is insignificant hence the resistance is fairly constant.
- As the p.d. across a filament lamp increases, current increases.
Heating effect is significant resulting in temperature increase. - The resistance of metals increases with temperature. Hence, decreasing $l-V$ gradient.
- In terms of the movement of charge carriers, the lattice ion vibrations will be more at higher temperature. There will be more reduction in the drift velocity of electrons due to collision with lattice ions hence current will be lower and resistance will be higher.
- In short, the resistance of a filament lamp increases as the p.d. applied across it increases.
The temperature characteristic of a thermistor
Thermistor $I-V$ characteristic and temperature characteristic
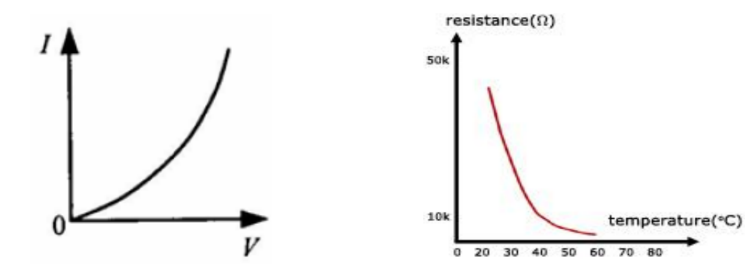
- A thermistor is a resistor made of semiconductors.
- With low p.d. across the thermistor, low current flowing through it and the heating effect is insignificant hence the resistance is fairly constant.
- As the p.d. across a thermistor increases, current increases.
Heating effect is significant resulting in temperature increase. - The resistance of semiconductors decreases with temperature. Hence, increasing $l-V$ gradient.
- In terms of the movement of charge carriers, the lattice ion vibrations will be more at higher temperature. There will be more reduction in the drift velocity of charge carriers due to collision with lattice ions. However the concentration of charge carriers in semiconductors increases significantly with temperature. Hence the overall effect is a reduction in resistance.
- In short, the resistance of a thermistor decreases as its temperature increases.
E.M.F in terms of the energy transferred by a source in driving unit charge round a complete circuit
Movement of charge carriers is possible only if they possess energy and are allowed to dissipate their energy. Sources like batteries and generators provide the energy to the charge carriers. Available path(s) for charge carriers to dissipate their energy cause their movement.
Defining in terms of energy:
The electromotive force (e.m.f.) of a source is defined as the non-electrical energy converted to electrical energy per unit charge driven through the source.
Defining in terms of power:
The electromotive force (e.m.f.) of a source is defined as the non-electrical power converted to electrical power per unit current delivered by the source.
The SI unit of e.m.f. is same as that of potential difference, i.e. the volt. (Recall that $1 \mathrm{~V}=1 \mathrm{~J} \mathrm{C}^{-1}$ or $1 \mathrm{~W} \mathrm{~A}^{-1}$ )
E.M.F in terms of the energy transferred by a source in driving unit charge round a complete circuit (continued from previous slide)
Mathematically, $E=\frac{W}{Q}$ or $E=\frac{P}{I}$
where $E$ is the e.m.f. of the source, in volts $(V)$
$W$ is the energy converted, in joules (J)
$Q$ is the electric charge moved, in coulombs (C)
$P$ is the power converted, in watts (W)
$I$ is the electric current delivered, in amperes (A)
Examples include:
- In a battery, chemical energy converted to electrical energy through chemical reactions.
- In a generator, mechanical energy (in the form of rotational kinetic energy) is converted to electrical energy.
Distinguish between e.m.f. and p.d. in terms of energy considerations
- The electromotive force (e.m.f.) of a source is defined using the non-electrical energy converted to electrical energy while the potential difference (p.d.) between two points is defined using electrical energy converted to non-electrical energy.
The effects of the internal resistance of a source of e.m.f. on the terminal potential difference and output power.
- In practice, no energy source (battery or generator) is perfect.
- Some of the electrical energy delivered by a source is always dissipated within itself.
- The source is said to have internal resistance. When the external load is large, the internal resistance has negligible effect.
- When the external load is not large, the internal resistance can be depicted as a series resistor within the source as shown in the diagram in next slide.
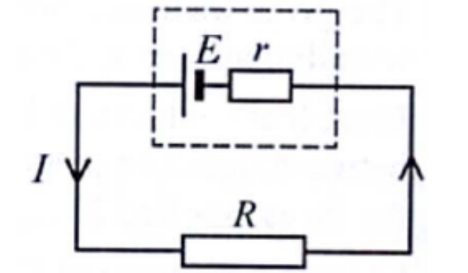
The energy delivered by the source is then shared between its internal resistance and external load,
i.e. energy supplied = energy dissipated (external + internal).
$\begin{array}{ll}E l t=I^2 R t+I^2 r t \\ \Rightarrow & E=I R+I r \\ \Rightarrow & E=I(R+r)\end{array}$
$\begin{gathered}E=V \\ V \times I=P\end{gathered}$
The terminal p.d. is the potential difference across the source. It is equivalent to the potential difference across the external circuit.
Hence terminal p.d. is $V=I R=E-I r$
where $V$ is the terminal p.d., in volts $(V)$
$E$ is the e.m.f. of the source, in volts (V)
$I$ is the electric current delivered, in amperes (A)
$R$ is the resistance of the external circuit, in ohms $(\Omega)$
$r$ is the internal resistance of the source, in ohms $(\Omega)$
The effects of the internal resistance of a source of e.m.f. on the terminal potential difference and output power. (continued from previous slide)
It can be deduced that when the source is connected to an external circuit, the terminal p.d. of the source is reduced by the amount $I r$.
V = E – Ir
When the current / through the source is zero (such as when the external circuit is open) then terminal p.d. $V$ will be equal to the e.m.f. $E$.
I in the above equation becomes Zero
When the internal resistance is negligible, the terminal p.d. will be approximately equal to the e.m.f. $E$.
Alternatively, viewing in terms of power, the power delivered by the source is shared between its internal resistance and external load,
i.e. power supplied = power dissipated (external + internal).
$
\begin{aligned}
& P_E=P_R+P_r \\
& E I=I^2 R+I^2 r
\end{aligned}
$
The power dissipated internally $\left(P_r=l^2 r\right)$ is wasted in heating up the energy source. Only the power that is dissipated externally $\left(P_R=l^2 R\right)$ is available to the external circuit so the efficiency of the source is always below $100 \%$.
$
\text { Efficiency } \eta=\frac{\text { useful power }}{\text { total power }}=\frac{V I}{E I}=\frac{I^2 R}{I^2(R+r)}=\frac{R}{R+r}
$
Show an understanding of the effects of the internal resistance of a source of e.m.f. on the terminal potential difference and output power.
Example 7
A battery of e.m.f. $12 \mathrm{~V}$ and internal resistance $0.014 \Omega$ delivers a 2.0 A current when first connected to a motor. Calculate the resistance of the motor.
Answer/Explanation
Solution:
$
E=I(R+r) \Rightarrow 12=2.0(R+0.014) \Rightarrow R=5.99 \Omega
$
