CIE IGCSE Physics (0625) Transformer Study Notes - New Syllabus
CIE IGCSE Physics (0625) Transformer Study Notes
LEARNING OBJECTIVE
- Understanding the concepts of Transformer
Key Concepts:
- Transformer Construction and Principle of Operation
- Use of Transformers in High-Voltage Transmission
Transformer Construction and Principle of Operation
Transformer Construction and Principle of Operation
Construction of a Simple Transformer:
- A transformer consists of two coils of insulated wire – the primary coil and the secondary coil.
- Both coils are wound on a common soft iron core, but are kept electrically isolated from each other.
- The iron core is laminated to reduce energy losses due to eddy currents.
- The soft iron core serves to efficiently carry the magnetic flux from the primary to the secondary coil.
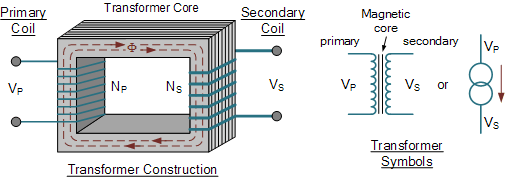
Principle of Operation:
- Based on electromagnetic induction: A changing magnetic field induces an e.m.f. in a nearby coil.
- An alternating voltage is applied to the primary coil.
- This produces a changing magnetic field in the soft iron core.
- The changing magnetic field links to the secondary coil, inducing an alternating e.m.f. in it.
- Note: A transformer only works with AC, not DC, because a changing magnetic field is required for induction.
Transformer: Key Terms
- Primary coil (p): The coil connected to the input voltage (usually from an a.c. power supply)
- Secondary coil (s): The coil connected to the output side, delivering the transformed voltage
- Step-up transformer: Increases the voltage – has more turns on the secondary coil than the primary coil (\(N_s > N_p\))
- Step-down transformer: Decreases the voltage – has fewer turns on the secondary coil than the primary coil (\(N_s < N_p\))
Transformer Equation (Ideal Transformer):
\(\dfrac{V_s}{V_p} = \dfrac{N_s}{N_p}\)
Where:
- \(V_s\) = voltage across secondary coil
- \(V_p\) = voltage across primary coil
- \(N_s\) = number of turns on secondary coil
- \(N_p\) = number of turns on primary coil
Energy Conservation:
In an ideal transformer (no energy losses):
\(V_p I_p = V_s I_s\)
But in practice, some energy is lost due to:
- Resistance of wires (heating)
- Eddy currents in the core (minimized by lamination)
- Magnetic flux leakage
Diagram of a Simple Transformer
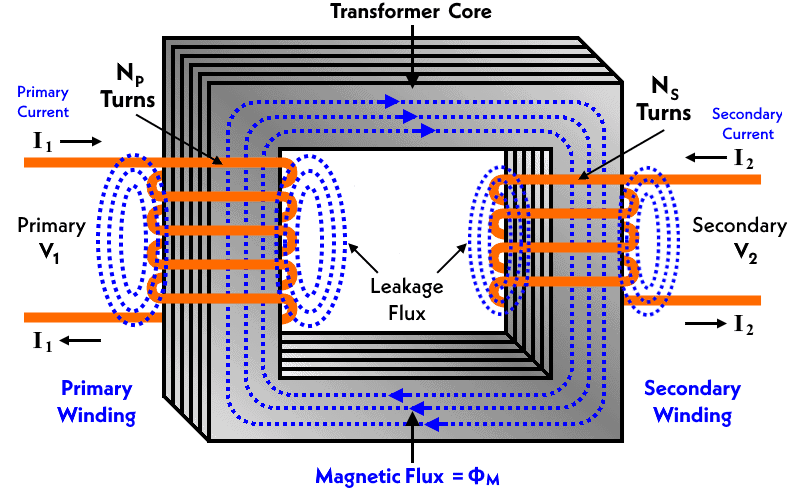
- Primary Coil (Np): Connected to the input a.c. source
- Secondary Coil (Ns): Connected to the output load
- Soft Iron Core: Enhances magnetic coupling
- Magnetic Flux: Travels through the iron core from primary to secondary
Example:
A transformer has 600 turns on the primary coil and 120 turns on the secondary coil. If the input voltage is 240 V a.c., calculate the output voltage.
▶️ Answer/Explanation
We use the transformer equation:
\(\dfrac{V_s}{V_p} = \dfrac{N_s}{N_p}\)
Substitute known values:
\(\dfrac{V_s}{240} = \dfrac{120}{600}\)
\(\Rightarrow V_s = 240 \times \dfrac{120}{600} = 48\,\text{V}\)
Type: Step-down transformer (because \(N_s < N_p\))
Final Answer: \(\boxed{48\,\text{V}}\)
Example:
A transformer is designed to increase voltage from 110 V to 220 V. If the primary coil has 200 turns, how many turns must the secondary coil have?
▶️ Answer/Explanation
Use the transformer equation:
\(\dfrac{V_s}{V_p} = \dfrac{N_s}{N_p}\)
Substitute known values:
\(\dfrac{220}{110} = \dfrac{N_s}{200}\)
\(\Rightarrow 2 = \dfrac{N_s}{200} \Rightarrow N_s = 400\)
Type: Step-up transformer (because \(N_s > N_p\))
Final Answer: \(\boxed{400\,\text{turns}}\)
Use of Transformers in High-Voltage Transmission
Use of Transformers in High-Voltage Transmission
Electricity is generated at power stations at moderate voltages (e.g. 11 kV).
- Step-up transformers are used to increase the voltage (e.g. to 132 kV or 400 kV) before transmission through power lines.
- High voltage means low current (since \( P = IV \), keeping power constant).
- This reduces the energy lost as heat in the transmission wires, as heat loss is given by:
\( \text{Power loss} = I^2 R \)
Power losses in cables are smaller when the voltage is higher, for a given amount of power being transmitted. This is because power loss in a cable is primarily due to the current flowing through it (specifically, I²R losses), and increasing the voltage allows for a reduction in current to transmit the same amount of power
- Near homes and industries, a step-down transformer reduces the voltage (e.g. to 230 V or 110 V) for safe use.

Advantages of High-Voltage Transmission
- Reduced energy loss: Less current is required to transmit the same amount of power, which reduces heating losses in cables.
- Thinner wires can be used: Since current is lower, wires do not need to be as thick, reducing costs.
- Improved transmission efficiency: More of the generated electrical energy reaches the end user.
Example:
A power station generates 200 kW of electrical power at 2,000 V. The power is transmitted through cables of total resistance 5 Ω.
Calculate:
- (a) The power loss during transmission without a step-up transformer.
- (b) The power loss if a step-up transformer is used to raise the voltage to 20,000 V before transmission, and a step-down transformer is used at the consumer end.
▶️ Answer/Explanation
(a)
Given power \( P = 200{,}000 \, \text{W} \), voltage \( V = 2{,}000 \, \text{V} \)
Using \( I = \frac{P}{V} = \frac{200{,}000}{2{,}000} = 100 \, \text{A} \)
Power loss in transmission cables:
\( P_{\text{loss}} = I^2 R = (100)^2 \times 5 = 50{,}000 \, \text{W} = 50 \, \text{kW} \)
(b)
Now \( I = \frac{P}{V} = \frac{200{,}000}{20{,}000} = 10 \, \text{A} \)
Power loss:
\( P_{\text{loss}} = I^2 R = (10)^2 \times 5 = 500 \, \text{W} \)
Interpretation: Using a step-up transformer reduces power loss from 50 kW to just 500 W.
