Edexcel iGCSE Physics -1.13–1.14 Scalars, Vectors, and Force as a Vector Quantity- Study Notes- New Syllabus
Edexcel iGCSE Physics -1.13–1.14 Scalars, Vectors, and Force as a Vector Quantity- Study Notes- New syllabus
Edexcel iGCSE Physics -1.13–1.14 Scalars, Vectors, and Force as a Vector Quantity- Study Notes -Edexcel iGCSE Physics – per latest Syllabus.
Key Concepts:
update
Scalar and Vector Quantities
Physical quantities can be divided into scalars and vectors. The key difference between them is whether direction is included.
Understanding this difference is essential when describing motion, forces, and changes in movement.
Scalar Quantities
A scalar quantity is a quantity that has magnitude only.
- Magnitude means size or amount.
- No direction is needed.
- Scalars are fully described by a single number and unit.
Examples of scalar quantities:
- Distance
- Speed
- Time
- Mass
- Energy
Vector Quantities
A vector quantity has both magnitude and direction.
- Direction tells us where the quantity is acting or moving.
- Vectors are often represented by arrows.
- The length of the arrow shows magnitude.
- The arrow direction shows direction.
Examples of vector quantities:
- Displacement
- Velocity
- Acceleration
- Force
- Momentum
Comparing Scalars and Vectors
- Speed tells how fast an object moves (scalar).
- Velocity tells how fast and in which direction an object moves (vector).
- Distance is the total path travelled (scalar).
- Displacement is the straight-line change in position with direction (vector).
Key Idea
- All vectors have direction; scalars do not.
- Two vectors with the same magnitude but different directions are not equal.
- Direction must always be stated for vector quantities.
Why This Difference Matters
- Forces must be added as vectors.
- Motion analysis often depends on direction.
- Ignoring direction can lead to incorrect answers.
Important Points to Remember
- Scalars can be added using normal arithmetic.
- Vectors must be added taking direction into account.
- Always check whether a quantity requires direction.
Example
A car travels at \( \mathrm{20\ m/s} \) east. State whether this quantity is scalar or vector.
▶️ Answer / Explanation
This is a vector quantity because it includes both speed and direction.
The quantity described is velocity.
Example
An object moves a distance of \( \mathrm{50\ m} \). State whether this quantity is scalar or vector.
▶️ Answer / Explanation
This is a scalar quantity because only magnitude is given.
No direction is stated.
Force as a Vector Quantity
A force is a push or a pull that can change the motion or shape of an object. Force is a vector quantity, which means it has both magnitude and direction.
Because force has direction, it must be treated differently from scalar quantities such as mass or time.
What Makes Force a Vector?
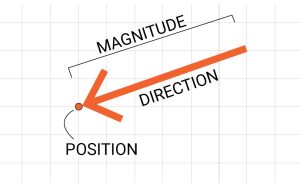
- Magnitude: how strong the force is (measured in newtons, N).
- Direction: the direction in which the force acts.
For a force to be fully described, both magnitude and direction must be stated.
Representing Forces
Forces are often represented using arrows:
- The length of the arrow shows the magnitude of the force.
- The arrowhead shows the direction of the force.
- The arrow starts at the point where the force acts.
This representation makes it easier to compare forces and find resultants.
Direction Matters
Two forces can have the same magnitude but produce different effects if they act in different directions.
- Forces in the same direction add together.
- Forces in opposite directions subtract.
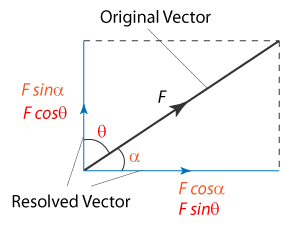
- Forces at angles must be resolved into components.
This is why forces cannot be added using simple arithmetic unless their directions are considered.
Resultant Force
The resultant force is the single force that has the same effect as all the forces acting together.
- If the resultant force is zero, the object is in equilibrium.
- If the resultant force is not zero, the object accelerates.
Key Idea
- Force has both size and direction.
- Direction affects motion and deformation.
- Forces must be added as vectors.
Important Points to Remember
- Always state the direction when giving a force.
- Forces are measured in newtons (N).
- Opposite forces can cancel each other.
Example
A force of \( \mathrm{10\ N} \) acts to the right on an object. Explain why this force is a vector.
▶️ Answer / Explanation
The force has a magnitude of \( \mathrm{10\ N} \) and a direction (to the right).
Because it has both magnitude and direction, it is a vector quantity.
Example
Two forces act on an object: \( \mathrm{8\ N} \) to the east and \( \mathrm{8\ N} \) to the west. State the resultant force.
▶️ Answer / Explanation
The forces have equal magnitude but opposite directions.
They cancel each other, so the resultant force is \( \mathrm{0\ N} \).