Edexcel iGCSE Physics -1.27P Conservation of Momentum- Study Notes- New Syllabus
Edexcel iGCSE Physics -1.27P Conservation of Momentum- Study Notes- New syllabus
Edexcel iGCSE Physics -1.27P Conservation of Momentum- Study Notes -Edexcel iGCSE Physics – per latest Syllabus.
Key Concepts:
update
Conservation of Momentum
The principle of conservation of momentum states that the total momentum of a system remains constant, provided that no external forces act on the system.
This principle is used to calculate the mass, velocity, or momentum of objects before or after collisions and explosions.
Momentum
Momentum is given by:
\( \mathrm{momentum = mass \times velocity} \)
\( \mathrm{p = mv} \)
- \( \mathrm{p} \) = momentum (kg m/s)
- \( \mathrm{m} \) = mass (kg)
- \( \mathrm{v} \) = velocity (m/s)
Principle of Conservation of Momentum
For a closed system:
\( \mathrm{total\ momentum\ before = total\ momentum\ after} \)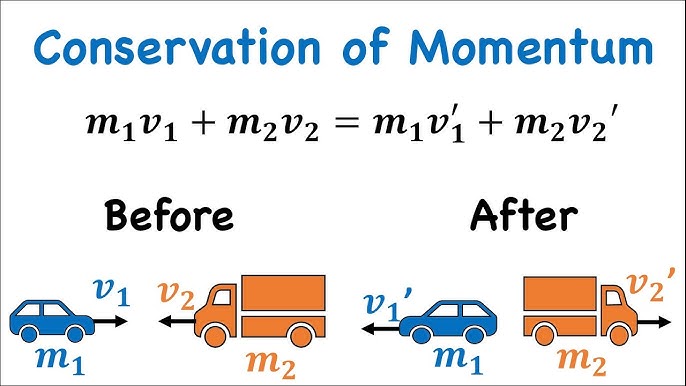
- Applies when no external forces act.
- Works for collisions and explosions.
- Direction must be taken into account.
Using Conservation of Momentum
- Choose a positive direction.
- Calculate total momentum before the event.
- Calculate total momentum after the event.
- Equate the two and solve.
Velocities in the opposite direction are taken as negative.
Key Equation (Two Objects)
For two objects moving along a straight line:
\( \mathrm{m_1u_1 + m_2u_2 = m_1v_1 + m_2v_2} \)
- \( \mathrm{u} \) = velocity before interaction
- \( \mathrm{v} \) = velocity after interaction
Types of Situations
- Collisions: objects hit and may stick together or move apart.
- Explosions: objects move apart from rest.
Key Idea
- Total momentum is conserved.
- Momentum is a vector quantity.
- Direction must always be considered.
Important Points to Remember
- Use velocities, not speeds.
- External forces break momentum conservation.
- Always include correct units.
Example
A trolley of mass \( \mathrm{2\ kg} \) moves at \( \mathrm{3\ m/s} \) and collides with a stationary trolley of mass \( \mathrm{4\ kg} \). They stick together after the collision. Calculate their common velocity.
▶️ Answer / Explanation
Initial momentum:
\( \mathrm{p = (2 \times 3) + (4 \times 0) = 6\ kg\,m/s} \)
After collision:
\( \mathrm{p = (2 + 4)v = 6v} \)
Using conservation of momentum:
\( \mathrm{6 = 6v} \)
\( \mathrm{v = 1\ m/s} \)
Example
Two objects collide head-on. Object A has mass \( \mathrm{1.5\ kg} \) and velocity \( \mathrm{4\ m/s} \). Object B has mass \( \mathrm{2.0\ kg} \) and velocity \( \mathrm{-2\ m/s} \). After the collision, object A stops. Calculate the velocity of object B.
▶️ Answer / Explanation
Total momentum before:
\( \mathrm{p = (1.5 \times 4) + (2.0 \times -2)} \)
\( \mathrm{p = 6 – 4 = 2\ kg\,m/s} \)
Total momentum after:
\( \mathrm{p = (1.5 \times 0) + (2.0 \times v)} = 2v \)
Using conservation of momentum:
\( \mathrm{2 = 2v} \)
\( \mathrm{v = 1\ m/s} \)