Edexcel iGCSE Physics -1.9–1.10 Distance from Velocity–Time Graphs and Motion Equations- Study Notes- New Syllabus
Edexcel iGCSE Physics -1.9–1.10 Distance from Velocity–Time Graphs and Motion Equations- Study Notes- New syllabus
Edexcel iGCSE Physics -1.9–1.10 Distance from Velocity–Time Graphs and Motion Equations- Study Notes -Edexcel iGCSE Physics – per latest Syllabus.
Key Concepts:
update
Distance from a Velocity–Time Graph
The distance travelled by an object can be determined from a velocity–time graph by finding the area between the graph and the time axis.
This method is especially useful when velocity is changing with time. 
Key Idea
On a velocity–time graph:
- The area under the graph represents the distance travelled.
- The time axis forms the base of the area.
- Distance is measured in metres (m).
This works because velocity multiplied by time gives distance.
Common Shapes and Areas
1. Rectangle (Constant Velocity)
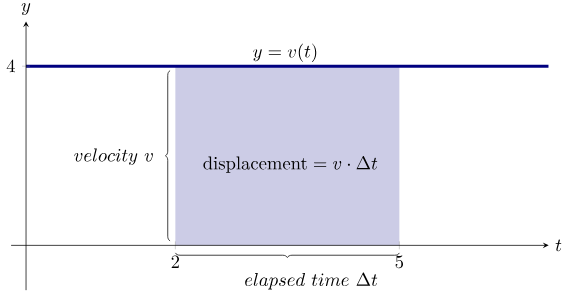
- Height = velocity
- Width = time
- Distance = velocity × time
\( \mathrm{distance = v \times t} \)
2. Triangle (Uniform Acceleration from Rest)
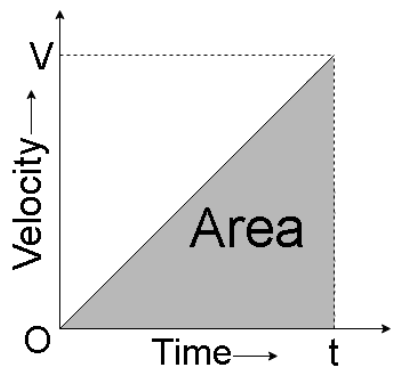
- Height = final velocity
- Base = time
- Distance = \( \dfrac{1}{2} \times base \times height \)
\( \mathrm{distance = \dfrac{1}{2}vt} \)
3. Trapezium (Changing Velocity)
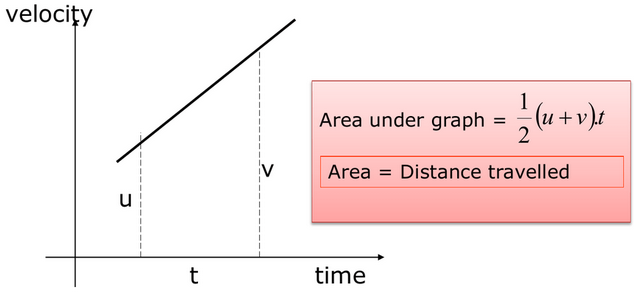
- Parallel sides = initial and final velocities
- Height = time
- Distance = average velocity × time
\( \mathrm{distance = \dfrac{(u + v)}{2} \times t} \)
Steps to Find Distance from a Velocity–Time Graph
- Identify the shape formed between the graph and the time axis.
- Split the area into simple shapes if necessary.
- Calculate the area of each shape.
- Add the areas together to find the total distance.
Important Points to Remember
- Distance is always positive.
- Read values carefully from the graph.
- Ensure time is in seconds and velocity in m/s.
Example
A velocity–time graph shows a constant velocity of \( \mathrm{8\ m/s} \) for \( \mathrm{6\ s} \). Calculate the distance travelled.
▶️ Answer / Explanation
The area under the graph is a rectangle.
Use: \( \mathrm{distance = v \times t} \)
\( \mathrm{distance = 8 \times 6} \)
\( \mathrm{distance = 48\ m} \)
Example
A velocity–time graph shows an object accelerating uniformly from rest to \( \mathrm{20\ m/s} \) in \( \mathrm{10\ s} \). Calculate the distance travelled.
▶️ Answer / Explanation
The area under the graph is a triangle.
Use: \( \mathrm{distance = \dfrac{1}{2}vt} \)
\( \mathrm{distance = \dfrac{1}{2} \times 20 \times 10} \)
\( \mathrm{distance = 100\ m} \)
Final Speed, Initial Speed, Acceleration and Distance
When an object moves with uniform acceleration, there is a direct relationship between its initial speed, final speed, acceleration, and the distance moved. This relationship allows distance or speed to be calculated without knowing the time taken.
This equation is commonly used to analyse motion in situations such as vehicles speeding up, slowing down, or objects falling under gravity.
Key Relationship
The relationship between final speed, initial speed, acceleration and distance moved is: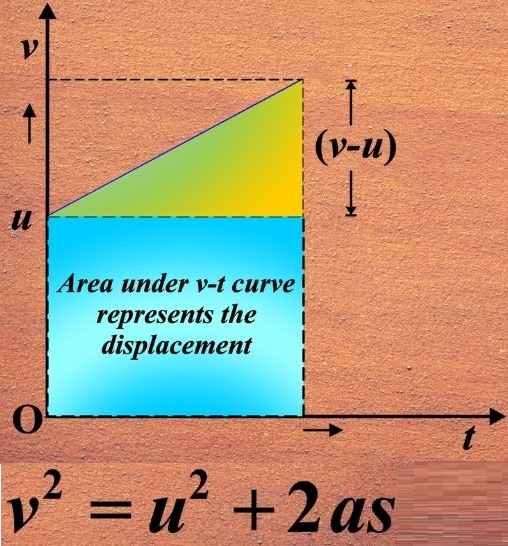
\( \mathrm{v^2 = u^2 + 2as} \)
- \( \mathrm{v} \) = final speed (m/s)
- \( \mathrm{u} \) = initial speed (m/s)
- \( \mathrm{a} \) = acceleration (m/s²)
- \( \mathrm{s} \) = distance moved (m)
Understanding the Equation
- This equation applies only when acceleration is constant.
- It links changes in speed directly to distance travelled.
- Time does not appear in this equation.
If acceleration is negative, the object is decelerating.
Rearranging the Equation
The equation can be rearranged to find other quantities:
- Distance moved: \( \mathrm{s = \dfrac{v^2 – u^2}{2a}} \)
- Acceleration: \( \mathrm{a = \dfrac{v^2 – u^2}{2s}} \)
- Initial speed: \( \mathrm{u = \sqrt{v^2 – 2as}} \)
When to Use This Equation
- When time is not given.
- When acceleration is constant.
- When motion is in a straight line.
Important Points to Remember
- Always use SI units.
- Square speeds carefully and include units at the end.
- Check signs for acceleration and velocity.
Example
A car accelerates uniformly from rest to a speed of \( \mathrm{20\ m/s} \) over a distance of \( \mathrm{50\ m} \). Calculate the acceleration of the car.
▶️ Answer / Explanation
Use: \( \mathrm{v^2 = u^2 + 2as} \)
\( \mathrm{20^2 = 0^2 + 2a(50)} \)
\( \mathrm{400 = 100a} \)
\( \mathrm{a = 4\ m/s^2} \)
Example
A cyclist slows down from \( \mathrm{15\ m/s} \) to \( \mathrm{5\ m/s} \) while travelling a distance of \( \mathrm{40\ m} \). Calculate the acceleration of the cyclist.
▶️ Answer / Explanation
Use: \( \mathrm{v^2 = u^2 + 2as} \)
\( \mathrm{5^2 = 15^2 + 2a(40)} \)
\( \mathrm{25 = 225 + 80a} \)
\( \mathrm{-200 = 80a} \)
\( \mathrm{a = -2.5\ m/s^2} \)
The negative value shows the cyclist is decelerating.
