Edexcel iGCSE Physics -2.13–2.15 Voltage, Current, Resistance, Charge, and Time- Study Notes- New Syllabus
Edexcel iGCSE Physics -2.13–2.15 Voltage, Current, Resistance, Charge, and Time- Study Notes- New syllabus
Edexcel iGCSE Physics -2.13–2.15 Voltage, Current, Resistance, Charge, and Time- Study Notes -Edexcel iGCSE Physics – per latest Syllabus.
Key Concepts:
update
Voltage, Current and Resistance (Ohm’s Law)
The relationship between voltage, current, and resistance describes how electric current flows in a circuit. This relationship is known as Ohm’s law.
Ohm’s law applies to components where the resistance remains constant, such as fixed resistors and metal wires at constant temperature.
Key Relationship (Ohm’s Law)
The relationship between voltage, current and resistance is: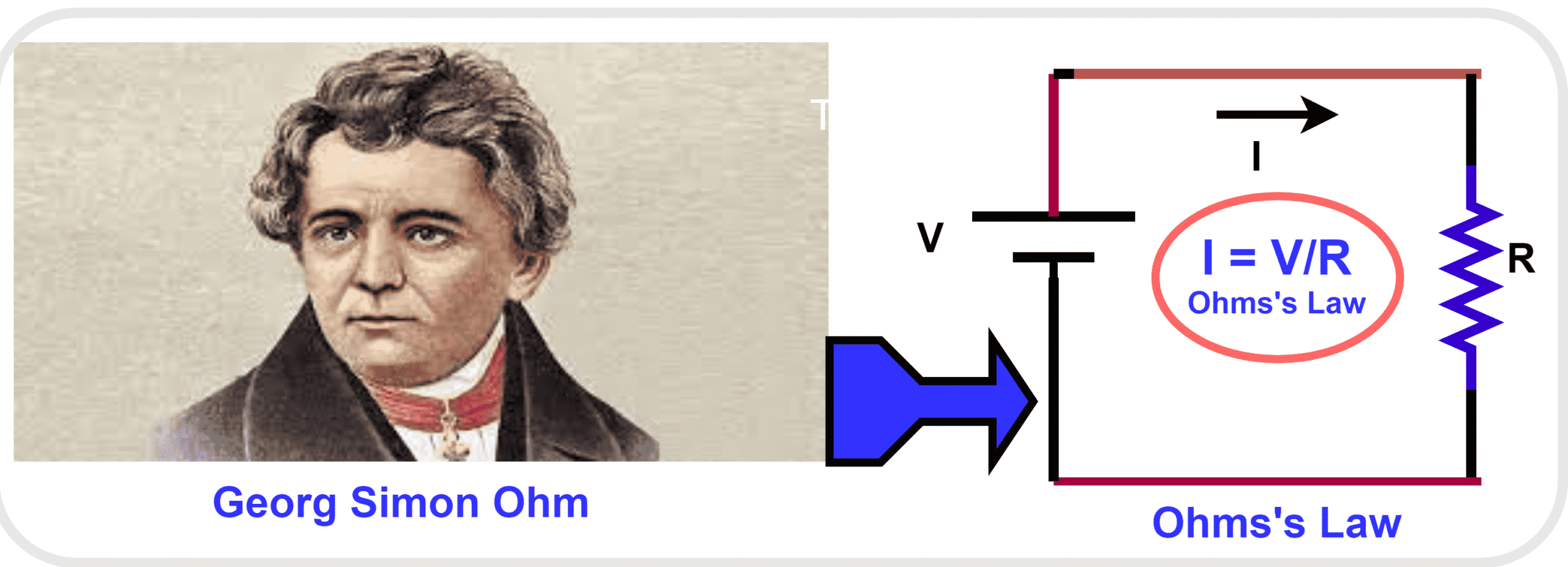
\( \mathrm{voltage = current \times resistance} \)
\( \mathrm{V = I \times R} \)
- \( \mathrm{V} \) = voltage (V)
- \( \mathrm{I} \) = current (A)
- \( \mathrm{R} \) = resistance (Ω)
Understanding the Equation
- Voltage provides the energy to push charge through a circuit.
- Resistance opposes the flow of charge.
- Current depends on both voltage and resistance.
For a fixed resistance, increasing the voltage increases the current.
Rearranging Ohm’s Law
Ohm’s law can be rearranged to calculate different quantities:
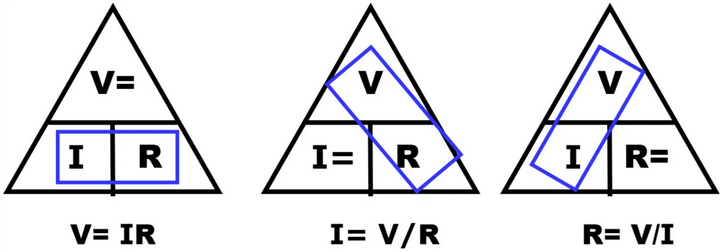
- Current: \( \mathrm{I = \dfrac{V}{R}} \)
- Resistance: \( \mathrm{R = \dfrac{V}{I}} \)
Conditions for Ohm’s Law
- The temperature of the component must be constant.
- The component must be ohmic.
- Filament lamps and diodes do not obey Ohm’s law.
Ohmic Conductors
Components that obey Ohm’s law are called ohmic conductors.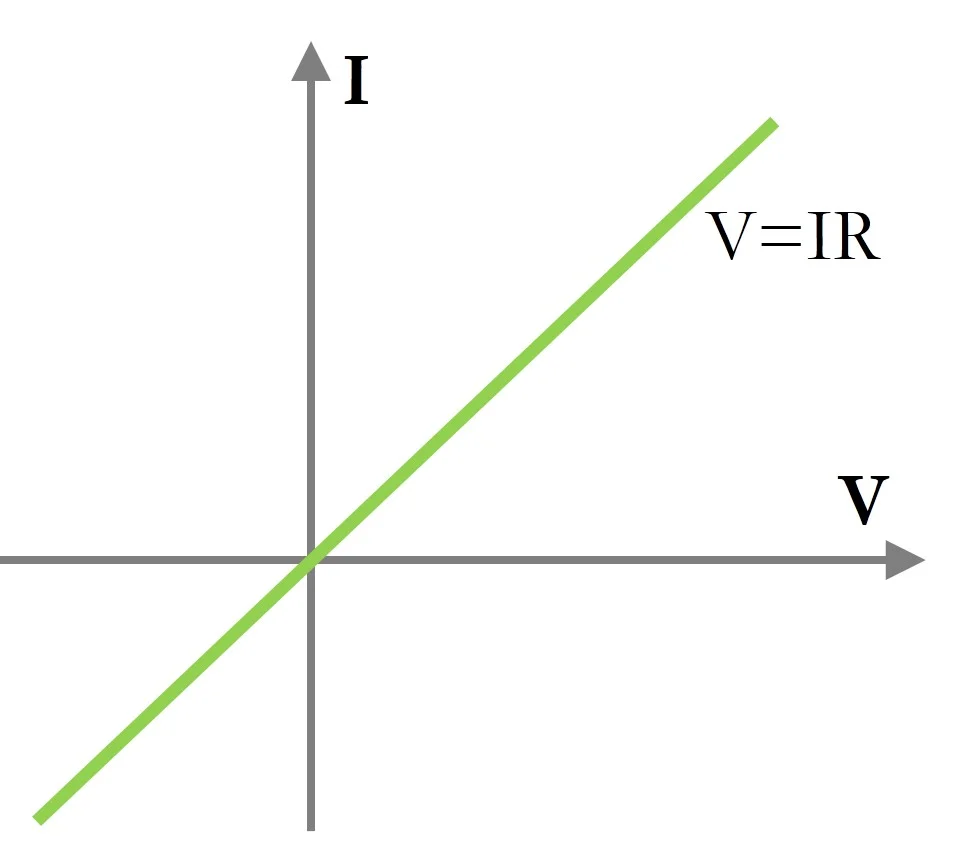
- Fixed resistors.
- Metal wires at constant temperature.
Their current–voltage graph is a straight line through the origin.
Key Idea
- Voltage, current and resistance are directly related.
- Ohm’s law links these three quantities.
- The law applies only to certain components.
Important Points to Remember
- Always use SI units.
- Check that Ohm’s law is applicable.
- Include units in final answers.
Example
A resistor has a resistance of \( \mathrm{10\ \Omega} \). A current of \( \mathrm{0.5\ A} \) flows through it. Calculate the voltage across the resistor.
▶️ Answer / Explanation
Use: \( \mathrm{V = IR} \)
\( \mathrm{V = 0.5 \times 10} \)
\( \mathrm{V = 5\ V} \)
Example
A component has a voltage of \( \mathrm{12\ V} \) across it and a current of \( \mathrm{3\ A} \). Calculate its resistance.
▶️ Answer / Explanation
Use: \( \mathrm{R = \dfrac{V}{I}} \)
\( \mathrm{R = \dfrac{12}{3}} \)
\( \mathrm{R = 4\ \Omega} \)
Electric Current
Electric current is the rate at which electric charge flows through a conductor or circuit.
This means current tells us how much charge passes a point in the circuit each second.
Key Relationship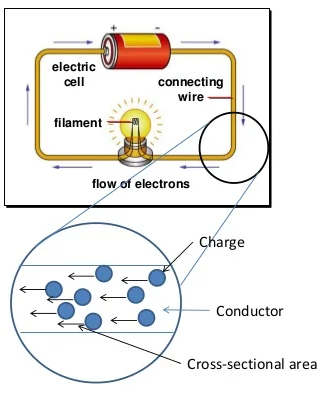
The relationship between current, charge, and time is:
\( \mathrm{current = \dfrac{charge}{time}} \)
\( \mathrm{I = \dfrac{Q}{t}} \)
- \( \mathrm{I} \) = current (A)
- \( \mathrm{Q} \) = charge (C)
- \( \mathrm{t} \) = time (s)
Meaning of the Equation
- A current of \( \mathrm{1\ A} \) means \( \mathrm{1\ C} \) of charge flows each second.
- A larger current means charge flows faster.
- No current means no charge is flowing.
Charge Flow in a Circuit
- In metal wires, charge is carried by electrons.
- Electrons move around a complete circuit.
- Current flows only when the circuit is closed.
Measuring Current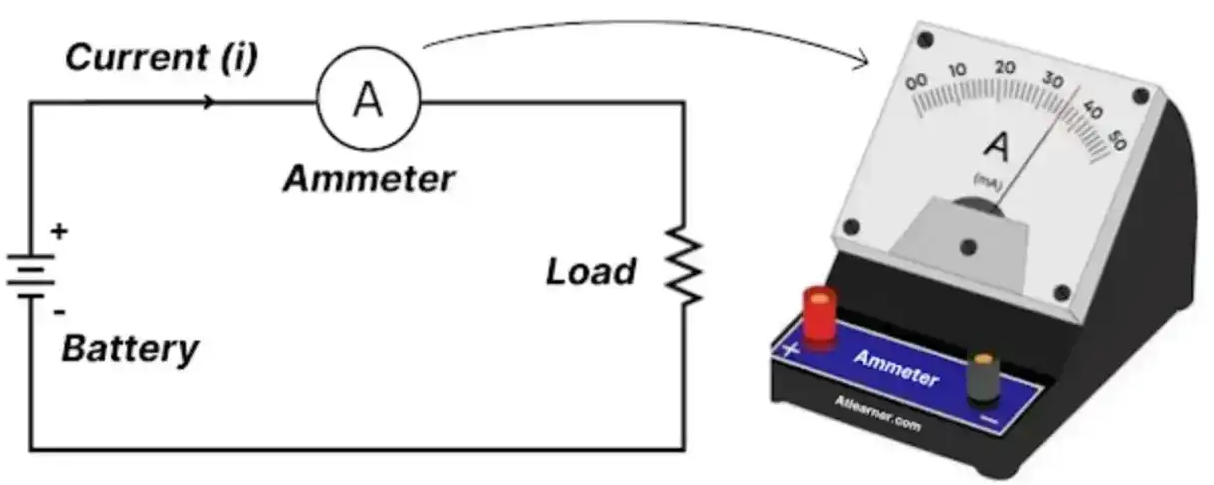
- Current is measured using an ammeter.
- The ammeter is connected in series.
- Units of current are amperes (A).
Key Idea
- Current measures how fast charge flows.
- It depends on charge and time.
- Current requires a complete circuit.
Important Points to Remember
- Current is not “used up” in a circuit.
- Charge flows continuously.
- Breaks in a circuit stop current flow.
Example
A charge of \( \mathrm{10\ C} \) flows past a point in a circuit in \( \mathrm{5\ s} \). Calculate the current.
▶️ Answer / Explanation
Use: \( \mathrm{I = \dfrac{Q}{t}} \)
\( \mathrm{I = \dfrac{10}{5}} \)
\( \mathrm{I = 2\ A} \)
Example
A current of \( \mathrm{3\ A} \) flows for \( \mathrm{4\ s} \). Calculate the charge transferred.
▶️ Answer / Explanation
Use: \( \mathrm{Q = It} \)
\( \mathrm{Q = 3 \times 4} \)
\( \mathrm{Q = 12\ C} \)
Charge, Current and Time
Electric charge is carried around a circuit when an electric current flows. The amount of charge transferred depends on the current and the time for which the current flows.
This relationship is fundamental to understanding how electrical energy is transferred in circuits.
Key Relationship
The relationship between charge, current and time is: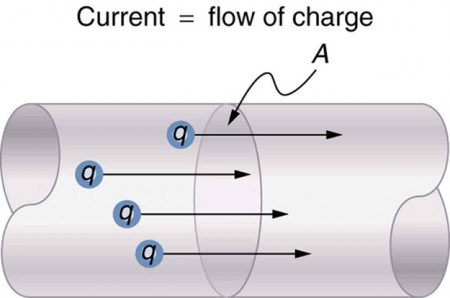
\( \mathrm{charge = current \times time} \)
\( \mathrm{Q = I \times t} \)
- \( \mathrm{Q} \) = charge (coulomb, C)
- \( \mathrm{I} \) = current (ampere, A)
- \( \mathrm{t} \) = time (second, s)
Understanding the Equation
- A larger current transfers more charge each second.
- A longer time allows more charge to flow.
- If no current flows, no charge is transferred.
A current of \( \mathrm{1\ A} \) means \( \mathrm{1\ C} \) of charge flows every second.
Rearranging the Equation
The equation can be rearranged to find current or time:
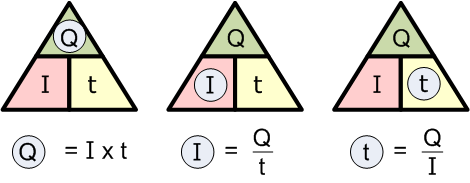
- Current: \( \mathrm{I = \dfrac{Q}{t}} \)
- Time: \( \mathrm{t = \dfrac{Q}{I}} \)
Charge Flow in Circuits
- In metal wires, charge is carried by electrons.
- Electrons move when the circuit is complete.
- Charge flows continuously around the circuit.
Key Idea
- Charge depends on current and time.
- More current or more time means more charge.
- This relationship applies to all electric circuits.
Important Points to Remember
- Charge is measured in coulombs.
- Time must be in seconds.
- Always include correct units.
Example
A current of \( \mathrm{3\ A} \) flows for \( \mathrm{10\ s} \). Calculate the charge transferred.
▶️ Answer / Explanation
Use: \( \mathrm{Q = It} \)
\( \mathrm{Q = 3 \times 10} \)
\( \mathrm{Q = 30\ C} \)
Example
A charge of \( \mathrm{20\ C} \) is transferred in \( \mathrm{5\ s} \). Calculate the current.
▶️ Answer / Explanation
Use: \( \mathrm{I = \dfrac{Q}{t}} \)
\( \mathrm{I = \dfrac{20}{5}} \)
\( \mathrm{I = 4\ A} \)