Edexcel iGCSE Physics -2.18–2.19 Voltage in Parallel Circuits and Series Circuit Calculations- Study Notes- New Syllabus
Edexcel iGCSE Physics -2.18–2.19 Voltage in Parallel Circuits and Series Circuit Calculations- Study Notes- New syllabus
Edexcel iGCSE Physics -2.18–2.19 Voltage in Parallel Circuits and Series Circuit Calculations- Study Notes -Edexcel iGCSE Physics – per latest Syllabus.
Key Concepts:
update
Voltage in Parallel Circuits
In a parallel circuit, components are connected on separate branches across the same power supply. The voltage across each component connected in parallel is the same.
This rule is essential for understanding why domestic electrical systems work reliably.
Key Relationship
For components connected in parallel:
\( \mathrm{V_{total} = V_1 = V_2 = V_3} \)
- \( \mathrm{V_{total}} \) = supply voltage (V)
- \( \mathrm{V_1, V_2, V_3} \) = voltage across each branch (V)
Why the Voltage Is the Same
- Each branch is connected directly across the power supply.
- Each component has the same two connection points as the supply.
- Therefore, each component experiences the full supply voltage.
No voltage is “used up” before reaching another branch.
Comparison with Series Circuits
- Parallel: voltage is the same across each component.
- Series: voltage is shared between components.
Practical Importance
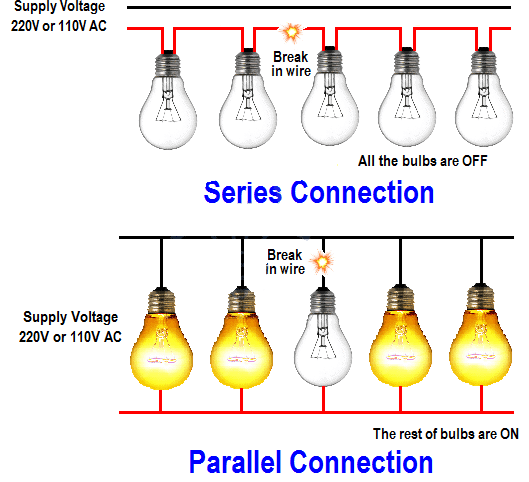
- Each appliance receives the correct operating voltage.
- Devices work independently.
- Failure of one component does not affect others.
This is why domestic lighting and sockets are wired in parallel.
Link to Current
Although voltage is the same in each branch:

- Current splits between branches.
- Total current equals the sum of branch currents.
This follows from current conservation at a junction.
Key Idea
- Parallel branches share the same voltage.
- Each component gets the full supply voltage.
- This allows independent operation.
Important Points to Remember
- Voltage does not change across parallel branches.
- Only current changes between branches.
- Use this rule when analysing parallel circuits.
Example
Two lamps are connected in parallel to a \( \mathrm{230\ V} \) supply. What is the voltage across each lamp?
▶️ Answer / Explanation
Each lamp is connected directly across the supply.
The voltage across each lamp is \( \mathrm{230\ V} \).
Example
A resistor and a lamp are connected in parallel across a battery. Explain why they have the same voltage across them.
▶️ Answer / Explanation
Both components are connected across the same two points.
Therefore, they experience the same potential difference.
Series Circuits: Calculating Current, Voltage and Resistance
In a series circuit, resistive components are connected end to end so that there is only one path for the current. The current, voltage, and resistance in the circuit are related in specific and predictable ways.
Key Rules for a Series Circuit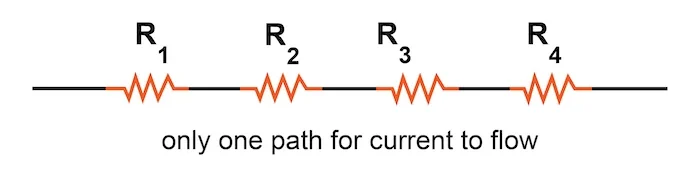
- The current is the same through all components.
- The total voltage is shared between components.
- The total resistance is the sum of individual resistances.
Total Resistance in Series
For two resistive components connected in series:
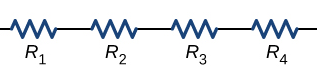
\( \mathrm{R_{total} = R_1 + R_2} \)
- \( \mathrm{R_{total}} \) = total resistance (Ω)
- \( \mathrm{R_1, R_2} \) = individual resistances (Ω)
Current in a Series Circuit
The current is the same everywhere in the circuit and is given by Ohm’s law:

\( \mathrm{I = \dfrac{V_{total}}{R_{total}}} \)
- \( \mathrm{I} \) = current (A)
- \( \mathrm{V_{total}} \) = supply voltage (V)
Voltage Across Each Component
The voltage across each resistor depends on its resistance:
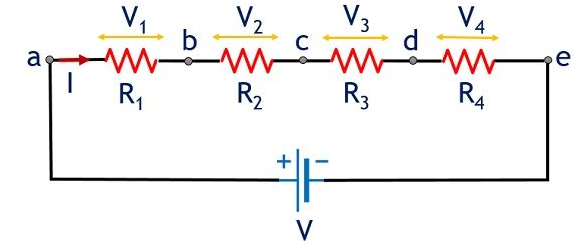
\( \mathrm{V = I \times R} \)
- Higher resistance → larger voltage drop.
- Lower resistance → smaller voltage drop.
The sum of the voltages equals the supply voltage:
\( \mathrm{V_{total} = V_1 + V_2} \)
Calculation Strategy
- Add resistances to find \( \mathrm{R_{total}} \).
- Calculate the current using \( \mathrm{I = V/R} \).
- Find voltage across each resistor using \( \mathrm{V = IR} \).
Key Idea
- Current is the same through all series components.
- Voltage is divided between components.
- Resistance adds directly.
Important Points to Remember
- Always use total resistance to find current.
- Check that voltages add up to the supply.
- Use SI units throughout.
Example
Two resistors of \( \mathrm{4\ \Omega} \) and \( \mathrm{6\ \Omega} \) are connected in series to a \( \mathrm{20\ V} \) supply.
(a) Calculate the total resistance. (b) Calculate the current in the circuit. (c) Calculate the voltage across each resistor.
▶️ Answer / Explanation
(a) Total resistance:
\( \mathrm{R_{total} = 4 + 6 = 10\ \Omega} \)
(b) Current:
\( \mathrm{I = \dfrac{20}{10} = 2\ A} \)
(c) Voltages:
\( \mathrm{V_1 = 2 \times 4 = 8\ V} \)
\( \mathrm{V_2 = 2 \times 6 = 12\ V} \)
Check: \( \mathrm{8 + 12 = 20\ V} \)
Example
Two resistors are connected in series to a \( \mathrm{12\ V} \) supply. The current in the circuit is \( \mathrm{0.5\ A} \). One resistor has a resistance of \( \mathrm{10\ \Omega} \).
Calculate the resistance of the second resistor.
▶️ Answer / Explanation
Total resistance:
\( \mathrm{R_{total} = \dfrac{V}{I} = \dfrac{12}{0.5} = 24\ \Omega} \)
Second resistor:
\( \mathrm{R_2 = 24 – 10 = 14\ \Omega} \)
