Edexcel iGCSE Physics -3.20–3.22 Total Internal Reflection, Critical Angle, and Refractive Index- Study Notes- New Syllabus
Edexcel iGCSE Physics -3.20–3.22 Total Internal Reflection, Critical Angle, and Refractive Index- Study Notes- New syllabus
Edexcel iGCSE Physics -3.20–3.22 Total Internal Reflection, Critical Angle, and Refractive Index- Study Notes -Edexcel iGCSE Physics – per latest Syllabus.
Key Concepts:
update
Total Internal Reflection in Optical Fibres and Prisms
Total internal reflection (TIR) occurs when light travelling in a denser medium reaches the boundary with a less dense medium at an angle greater than the critical angle. Instead of refracting out, the light is completely reflected back into the denser medium.
Conditions for Total Internal Reflection
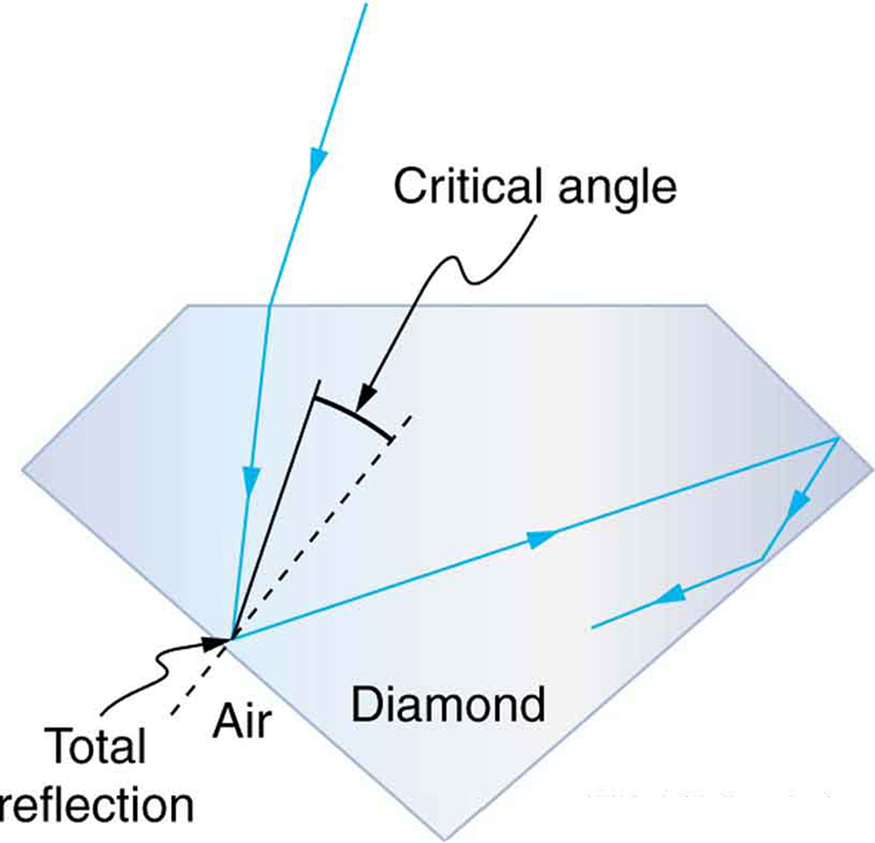
- Light must travel from a denser medium to a less dense medium.
- The angle of incidence must be greater than the critical angle.
If either condition is not met, total internal reflection does not occur.
Relevant Relationship
The critical angle is related to refractive index:
\( \mathrm{\sin c = \dfrac{1}{n}} \)
- \( \mathrm{c} \) = critical angle (°)
- \( \mathrm{n} \) = refractive index of the denser medium
Total Internal Reflection in Optical Fibres
Optical fibres are long, thin strands of glass or plastic used to transmit information such as data, images, and telephone signals.
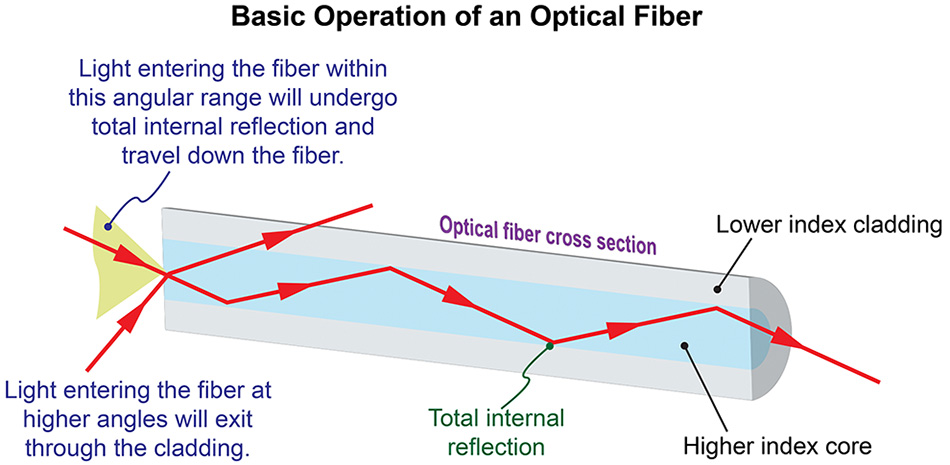
- Light enters the fibre at a suitable angle.
- The core of the fibre has a higher refractive index than the surrounding cladding.
- Light repeatedly undergoes total internal reflection at the core–cladding boundary.
- This keeps the light trapped inside the fibre.
Why this is useful:
- Signals can travel long distances with little energy loss.
- Information can be transmitted quickly as pulses of light.
- Fibres are thin, flexible, and secure.
Applications:
- Internet and telephone communications
- Medical endoscopes
- High-speed data transmission
Total Internal Reflection in Prisms
Prisms use total internal reflection to change the direction of light accurately.
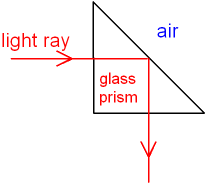
- Light enters the prism and reaches an internal face.
- The angle of incidence inside the prism is greater than the critical angle.
- The light is totally internally reflected.
Why prisms are used instead of mirrors:
- TIR gives nearly 100% reflection.
- No loss of brightness due to absorption.
- Produces precise and reliable reflections.
Applications:
- Periscopes
- Binoculars
- Cameras
Key Differences: Optical Fibres vs Prisms
| Optical Fibres | Prisms |
|---|---|
| Transmit information | Change direction of light |
| Multiple reflections | Single controlled reflection |
| Flexible | Rigid glass block |
Key Idea
- Total internal reflection keeps light trapped.
- Optical fibres use TIR to transmit information.
- Prisms use TIR for accurate reflection.
Important Points to Remember
- TIR only happens above the critical angle.
- Light must go from denser to less dense medium.
- TIR is more efficient than mirror reflection.
Example
Explain how total internal reflection allows information to be transmitted along an optical fibre.
▶️ Answer / Explanation
Light travels inside the fibre core and strikes the boundary with the cladding at angles greater than the critical angle.
This causes repeated total internal reflection, keeping the light inside the fibre so information can travel long distances.
Example
Prisms are often used instead of mirrors in binoculars.
Explain why.
▶️ Answer / Explanation
Prisms use total internal reflection, which reflects almost all the light.
This produces brighter images than mirrors, which absorb some light.
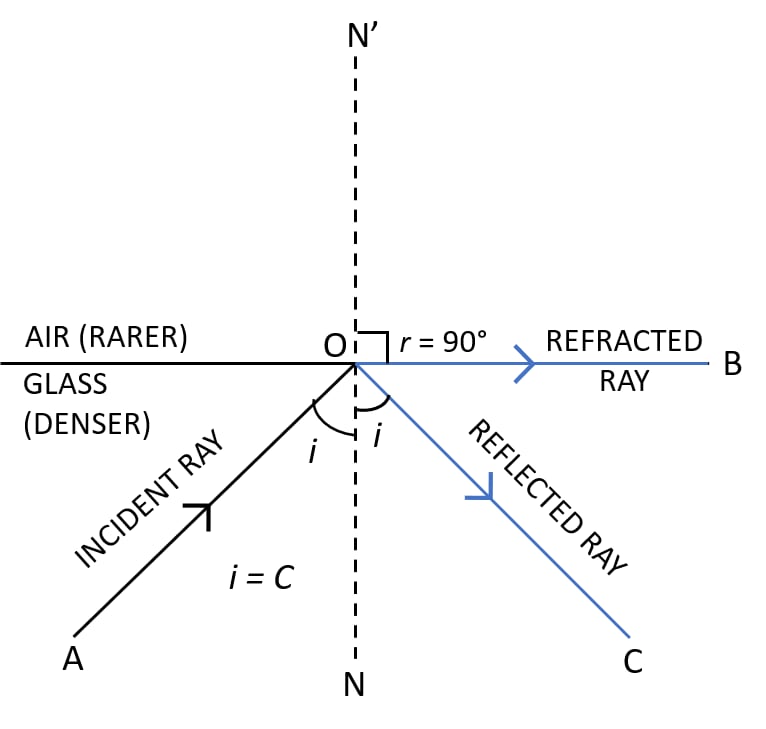
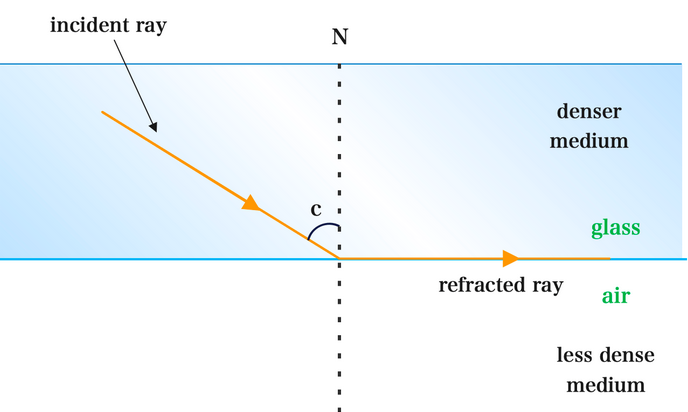
Critical Angle (c)
The critical angle, symbol \( \mathrm{c} \), is the angle of incidence in the denser medium for which the angle of refraction in the less dense medium is 90°.
At this angle, the refracted ray travels along the boundary between the two media.
Definition of Critical Angle
- The critical angle is measured from the normal.
- It occurs when light travels from a denser medium to a less dense medium.
- The refracted ray makes an angle of 90° with the normal.
At the critical angle:
- Refraction still occurs.
- The refracted ray runs along the surface.
- Total internal reflection has not yet started.
What Happens at Different Angles
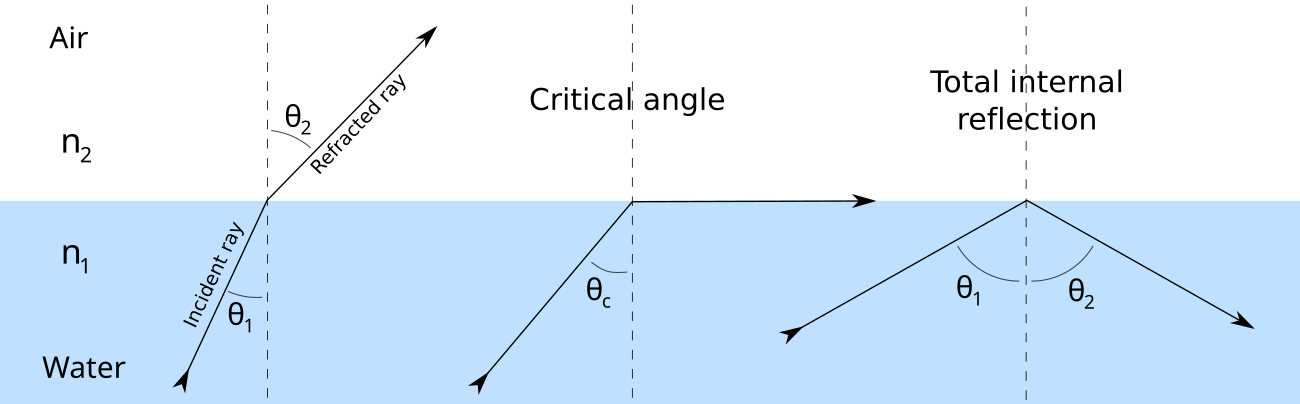
- Angle of incidence less than c: light is refracted out.
- Angle of incidence equal to c: refracted ray travels along the boundary.
- Angle of incidence greater than c: total internal reflection occurs.
Conditions Required for a Critical Angle
- Light must travel from a denser medium to a less dense medium.
- The refractive index of the denser medium must be greater than the less dense medium.
Relevant Formula
The critical angle is related to refractive index:
\( \mathrm{\sin c = \dfrac{1}{n}} \)
- \( \mathrm{c} \) = critical angle (°)
- \( \mathrm{n} \) = refractive index of the denser medium
Understanding the Formula
- A higher refractive index gives a smaller critical angle.
- If \( \mathrm{n} \) increases, \( \mathrm{c} \) decreases.
- This explains why glass has a smaller critical angle than water.
Key Idea
- The critical angle marks the boundary between refraction and total internal reflection.
- It is a fixed value for a given pair of media.
- Measured from the normal inside the denser medium.
Important Points to Remember
- Critical angle only exists when light goes from denser to less dense medium.
- Angles are always measured from the normal.
- Total internal reflection only occurs above the critical angle.
Example
Define the critical angle.
▶️ Answer / Explanation
The critical angle is the angle of incidence in the denser medium for which the angle of refraction in the less dense medium is 90°.
Example
The refractive index of glass is \( \mathrm{1.50} \).
Explain what happens when light in the glass strikes the glass–air boundary at an angle greater than the critical angle.
▶️ Answer / Explanation
The light does not refract out of the glass.
Instead, it undergoes total internal reflection and remains inside the glass.
Critical Angle and Refractive Index
The critical angle, symbol \( \mathrm{c} \), is directly related to the refractive index of a material. This relationship allows the critical angle to be calculated if the refractive index is known, and vice versa.
Conditions for Critical Angle
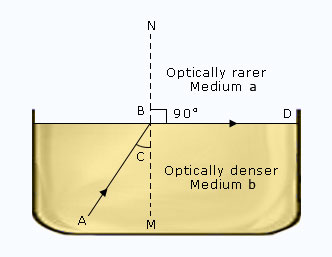
- Light must travel from a denser medium to a less dense medium.
- The angle of incidence is measured in the denser medium.
- The angle of refraction in the less dense medium is \( \mathrm{90^\circ} \).
Relationship Between Critical Angle and Refractive Index
The mathematical relationship is:
\( \mathrm{\sin c = \dfrac{1}{n}} \)
- \( \mathrm{c} \) = critical angle (°)
- \( \mathrm{n} \) = refractive index of the denser medium (relative to air)
This equation is derived from Snell’s law when the angle of refraction is \( \mathrm{90^\circ} \).
Understanding the Relationship
- A higher refractive index means light slows down more.
- As refractive index increases, the critical angle decreases.
- Materials with high refractive index have small critical angles.
Example values:
- Glass (\( \mathrm{n \approx 1.5} \)) → \( \mathrm{c \approx 42^\circ} \)
- Water (\( \mathrm{n \approx 1.33} \)) → \( \mathrm{c \approx 49^\circ} \)
Why This Relationship Is Important
- Used to design optical fibres.
- Determines when total internal reflection occurs.
- Used in prism calculations and applications.
Key Idea
- The critical angle depends only on refractive index.
- Total internal reflection occurs only when the angle of incidence is greater than the critical angle.
- This relationship applies only for light going from denser to less dense medium.
Important Points to Remember
- Critical angle has no meaning if light travels from less dense to denser medium.
- Angles must be measured from the normal.
- Refractive index has no unit.
Example
The refractive index of glass is \( \mathrm{1.50} \).
Calculate the critical angle for light travelling from glass into air.
▶️ Answer / Explanation
Use the formula:
\( \mathrm{\sin c = \dfrac{1}{n}} \)
\( \mathrm{\sin c = \dfrac{1}{1.50} = 0.667} \)
\( \mathrm{c = \sin^{-1}(0.667)} \)
\( \mathrm{c \approx 41.8^\circ} \)
Example
The critical angle for a material is \( \mathrm{48^\circ} \).
Calculate the refractive index of the material.
▶️ Answer / Explanation
Use:
\( \mathrm{\sin c = \dfrac{1}{n}} \)
Rearrange:
\( \mathrm{n = \dfrac{1}{\sin c}} \)
\( \mathrm{n = \dfrac{1}{\sin 48^\circ}} \)
\( \mathrm{n = \dfrac{1}{0.743}} \)
\( \mathrm{n \approx 1.35} \)