Edexcel iGCSE Physics -3.5–3.6 Wave Speed, Frequency, Wavelength, and Time Period- Study Notes- New Syllabus
Edexcel iGCSE Physics -Link- Study Notes- New syllabus
Edexcel iGCSE Physics -Link- Study Notes -Edexcel iGCSE Physics – per latest Syllabus.
Key Concepts:
3.5 know and use the relationship between the speed, frequency and wavelength of a wave:
wave speed = frequency × wavelength
v = f × λ
3.6 use the relationship between frequency and time period:
frequency = 1 / time period
f = 1 / T
Wave Speed, Frequency and Wavelength
The speed at which a wave travels depends on how frequently the wave oscillates and the distance between successive wavefronts. This relationship applies to all types of waves, including sound waves, water waves, and electromagnetic waves.
Key Relationship
The relationship between wave speed, frequency and wavelength is:
\( \mathrm{wave\ speed = frequency \times wavelength} \)
\( \mathrm{v = f \times \lambda} \)
- \( \mathrm{v} \) = wave speed (m/s)
- \( \mathrm{f} \) = frequency (Hz)
- \( \mathrm{\lambda} \) = wavelength (m)
Understanding the Equation
- Frequency tells how many waves pass a point each second.
- Wavelength tells how long each wave is.
- Multiplying them gives the distance travelled per second.
This distance per second is the wave speed.
What Happens if One Quantity Changes
- If frequency increases and wave speed stays constant, wavelength decreases.
- If wavelength increases and wave speed stays constant, frequency decreases.
- In a given medium, wave speed is usually constant.
Applies to Different Types of Waves
- Sound waves: speed depends on the medium.
- Water waves: speed depends on water depth.
- Light waves: speed depends on the medium (vacuum or material).
Key Idea
- Wave speed links frequency and wavelength.

- The equation works for all waves.
- Correct units must always be used.
Important Points to Remember
- Use Hz for frequency and metres for wavelength.
- Wave speed is always in m/s.
- Rearrange the equation carefully when needed.
Rearranging the Formula
- Frequency: \( \mathrm{f = \dfrac{v}{\lambda}} \)
- Wavelength: \( \mathrm{\lambda = \dfrac{v}{f}} \)
Example
A water wave has a frequency of \( \mathrm{2.5\ Hz} \) and a wavelength of \( \mathrm{0.40\ m} \).
Calculate the speed of the wave.
▶️ Answer / Explanation
Use: \( \mathrm{v = f\lambda} \)
\( \mathrm{v = 2.5 \times 0.40} \)
\( \mathrm{v = 1.0\ m/s} \)
The correct unit for wave speed is m/s.
Example
Sound waves travel through air at a speed of \( \mathrm{340\ m/s} \).
If the frequency of the sound is \( \mathrm{680\ Hz} \), calculate the wavelength.
▶️ Answer / Explanation
Rearrange: \( \mathrm{\lambda = \dfrac{v}{f}} \)
\( \mathrm{\lambda = \dfrac{340}{680}} \)
\( \mathrm{\lambda = 0.50\ m} \)
This wavelength matches a sound wave in air.
Relationship Between Frequency and Time Period
Waves and oscillations can be described using two closely related quantities: frequency and time period. These quantities describe how often a vibration or wave repeats.
Frequency
The frequency of a wave or oscillation is the number of complete oscillations passing a point each second.
![]()
- Measured in hertz (Hz).
- 1 Hz means one oscillation per second.
Time Period
The time period is the time taken for one complete oscillation.
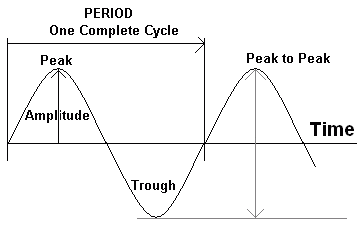
- Measured in seconds (s).
- Represents the duration of one cycle.
Key Relationship
Frequency and time period are reciprocals of each other.
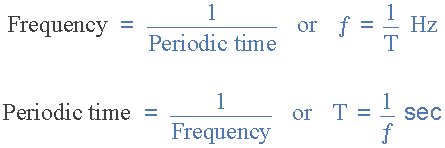
\( \mathrm{frequency = \dfrac{1}{time\ period}} \)
\( \mathrm{f = \dfrac{1}{T}} \)
Rearranging:
\( \mathrm{T = \dfrac{1}{f}} \)
- \( \mathrm{f} \) = frequency (Hz)
- \( \mathrm{T} \) = time period (s)
Understanding the Relationship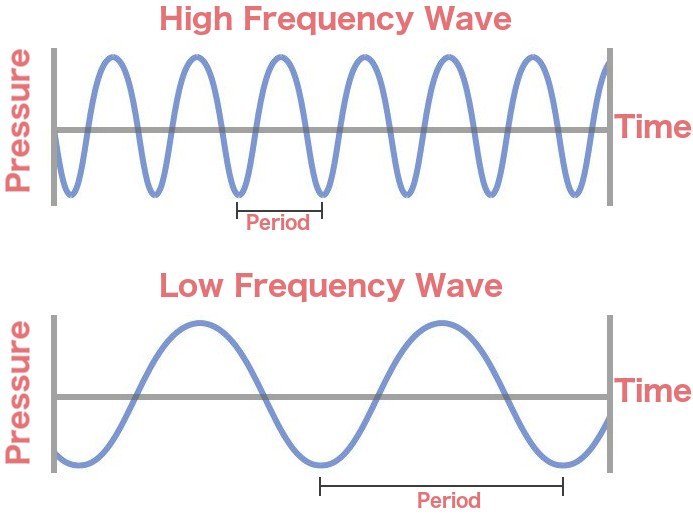
- A high frequency means many oscillations per second.
- This results in a short time period.
- A low frequency means fewer oscillations per second.
- This results in a long time period.
Connection to Waves
- Frequency determines pitch of sound.
- Time period determines how long one vibration lasts.
- Both describe the same oscillatory motion.
Key Idea
- Frequency and period describe repetition.
- They are inversely related.
- Only one is needed to calculate the other.
Important Points to Remember
- Always convert units correctly.
- Use seconds for period.
- Use hertz for frequency.
Example
A vibrating object has a frequency of \( \mathrm{20\ Hz} \).
(a) Define the time period. (b) Calculate the time period of the vibration.
▶️ Answer / Explanation
(a) The time period is the time taken for one complete oscillation.
(b) Use \( \mathrm{T = \dfrac{1}{f}} \):
\( \mathrm{T = \dfrac{1}{20} = 0.050\ s} \)
Example
A wave has a time period of \( \mathrm{0.004\ s} \).
(a) Calculate the frequency of the wave. (b) State the unit of frequency.
▶️ Answer / Explanation
(a) Use \( \mathrm{f = \dfrac{1}{T}} \):
\( \mathrm{f = \dfrac{1}{0.004} = 250\ Hz} \)
(b) The unit of frequency is hertz (Hz).
