Edexcel iGCSE Physics -3.7 Wave Relationships in Different Contexts- Study Notes- New Syllabus

Using Wave Relationships in Different Contexts

The same mathematical relationships apply to all types of waves. These relationships can be used to analyse sound waves (mechanical waves) and electromagnetic waves such as radio waves and light.

Although the nature of these waves is different, the equations linking speed, frequency, wavelength, and time period are the same.

Key Wave Relationships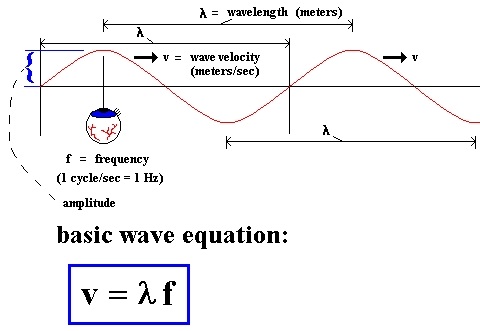

The main wave equation is:

\( \mathrm{v = f\lambda} \)

• \( \mathrm{v} \) = wave speed (m/s)
• \( \mathrm{f} \) = frequency (Hz)
• \( \mathrm{\lambda} \) = wavelength (m)

The relationship between frequency and time period is:

\( \mathrm{f = \dfrac{1}{T}} \)

\( \mathrm{T = \dfrac{1}{f}} \)

• \( \mathrm{T} \) = time period (s)

Using the Relationships for Sound Waves

Sound waves are longitudinal waves that require a medium such as air to travel.

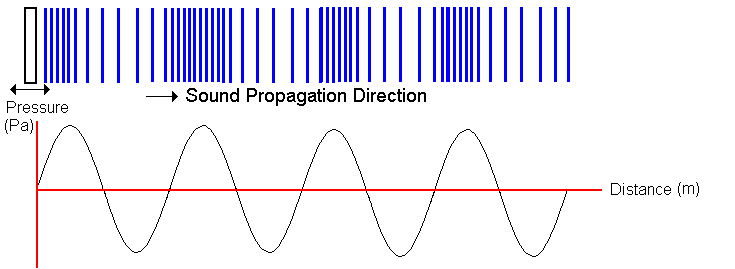
• In air, sound travels at approximately \( \mathrm{340\ m/s} \).
• Higher frequency → higher pitch.
• Wavelength changes if frequency changes but speed stays constant.

Application: Calculating wavelength of sound in air.

Using the Relationships for Electromagnetic Waves

Electromagnetic waves are transverse waves and do not require a medium.

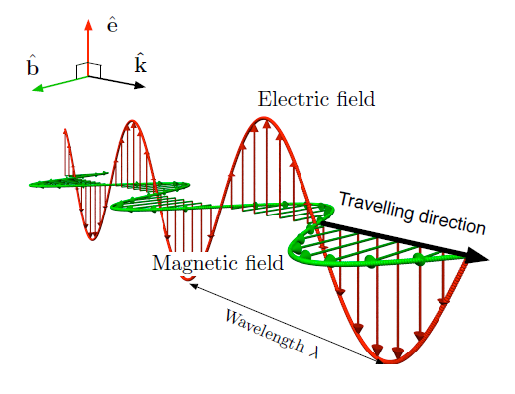
• All EM waves travel at the same speed in a vacuum.
• Speed in a vacuum: \( \mathrm{3.0 \times 10^8\ m/s} \).
• Higher frequency → shorter wavelength.

Application: Calculating wavelength of radio waves or light.

Comparing the Contexts

• The equations are identical for sound and EM waves.
• The wave speed depends on the type of wave and medium.
• Frequency and wavelength are linked through speed.

Key Idea

• One set of equations works for all waves.
• Only the wave speed changes between contexts.
• Correct units are essential.

Important Points to Remember

• Sound cannot travel in a vacuum.
• Electromagnetic waves can.
• Always check which quantity is constant.