Edexcel iGCSE Physics -5.12–5.13P Specific Heat Capacity and Thermal Energy Change Equation- Study Notes- New Syllabus
Edexcel iGCSE Physics -5.12–5.13P Specific Heat Capacity and Thermal Energy Change Equation- Study Notes- New syllabus
Edexcel iGCSE Physics -5.12–5.13P Specific Heat Capacity and Thermal Energy Change Equation- Study Notes -Edexcel iGCSE Physics – per latest Syllabus.
Key Concepts:
update
Specific Heat Capacity
Specific heat capacity is a property of a material that tells us how much energy is needed to change its temperature.
It is defined as:
The energy required to change the temperature of 1 kilogram of a substance by 1 degree Celsius.
Unit of Specific Heat Capacity
joules per kilogram per degree Celsius (J/kg °C)
This unit shows that:
- Energy is measured in joules (J)
- Mass is measured in kilograms (kg)
- Temperature change is measured in degrees Celsius (°C)
Meaning of Specific Heat Capacity
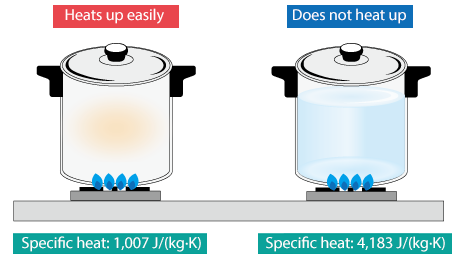
- A material with a high specific heat capacity needs a lot of energy to warm up.
- A material with a low specific heat capacity heats up quickly.
Example: Water has a high specific heat capacity, which is why it heats up slowly and is useful for cooling systems.
Relationship Involving Specific Heat Capacity
The energy transferred when the temperature of a substance changes is given by:
\( \mathrm{E = mc\Delta T} \)
- \( \mathrm{E} \) = energy transferred (J)
- \( \mathrm{m} \) = mass (kg)
- \( \mathrm{c} \) = specific heat capacity (J/kg °C)
- \( \mathrm{\Delta T} \) = temperature change (°C)
Energy Store Explanation
- Heating transfers energy to the internal energy store.
- This increases the kinetic energy of particles.
- An increase in kinetic energy causes temperature to rise.
Key Idea
- Specific heat capacity depends on the material.
- It tells us how hard a substance is to heat up.
- Measured in J/kg °C.
Important Points to Remember
- Temperature change, not final temperature, is used.
- Mass must be in kilograms.
- Energy must be in joules.
Example
Aluminium has a specific heat capacity of \( \mathrm{900\ J/kg\,^\circ C} \).
Explain what this value means.
▶️ Answer / Explanation
It means that 900 joules of energy are required to raise the temperature of 1 kg of aluminium by 1 °C.
Example
Two blocks of equal mass are heated with the same amount of energy.
Block A shows a smaller temperature rise than Block B.
State which block has the higher specific heat capacity and explain why.
▶️ Answer / Explanation
Block A has the higher specific heat capacity.
This is because it requires more energy per kilogram per degree Celsius to raise its temperature.
Change in Thermal Energy
When a substance is heated or cooled, its thermal energy changes. The amount of thermal energy transferred depends on the mass of the substance, its specific heat capacity, and the change in temperature.
Equation for Change in Thermal Energy
The relationship is:
change in thermal energy = mass × specific heat capacity × change in temperature
\( \mathrm{\Delta E = m c \Delta T} \)
- \( \mathrm{\Delta E} \) = change in thermal energy (joule, J)
- \( \mathrm{m} \) = mass (kilogram, kg)
- \( \mathrm{c} \) = specific heat capacity (J/kg °C)
- \( \mathrm{\Delta T} \) = temperature change (°C)
Understanding the Equation
- Increasing mass increases energy needed.
- Materials with higher specific heat capacity need more energy.
- Larger temperature change requires more energy.
This explains why water takes a long time to heat up compared to metals.
Energy Store Explanation
- Heating transfers energy to the internal energy store.
- This increases the kinetic energy of particles.
- An increase in kinetic energy causes temperature to rise.
Rearranging the Equation
- Mass: \( \mathrm{m = \dfrac{\Delta E}{c \Delta T}} \)
- Specific heat capacity: \( \mathrm{c = \dfrac{\Delta E}{m \Delta T}} \)
- Temperature change: \( \mathrm{\Delta T = \dfrac{\Delta E}{m c}} \)
Key Idea
- Thermal energy change depends on material and temperature change.
- The equation applies when no change of state occurs.
- Units must be consistent.
Important Points to Remember
- Use kilograms, not grams.
- Use temperature change, not final temperature.
- Energy is measured in joules.
Example
A block of copper has a mass of \( \mathrm{1.5\ kg} \) and a specific heat capacity of \( \mathrm{390\ J/kg\,^\circ C} \).
Calculate the change in thermal energy when its temperature rises by \( \mathrm{20^\circ C} \).
▶️ Answer / Explanation
Use:
\( \mathrm{\Delta E = m c \Delta T} \)
\( \mathrm{\Delta E = 1.5 \times 390 \times 20} \)
\( \mathrm{\Delta E = 11\,700\ J} \)
Example
Water has a specific heat capacity of \( \mathrm{4200\ J/kg\,^\circ C} \).
How much energy is required to raise the temperature of \( \mathrm{0.80\ kg} \) of water by \( \mathrm{15^\circ C} \)?
▶️ Answer / Explanation
Use:
\( \mathrm{\Delta E = m c \Delta T} \)
\( \mathrm{\Delta E = 0.80 \times 4200 \times 15} \)
\( \mathrm{\Delta E = 50\,400\ J} \)