Edexcel iGCSE Physics -5.20–5.22 Gas Pressure Relationships (Pressure–Temperature and Pressure–Volume)- Study Notes- New Syllabus
Edexcel iGCSE Physics -5.20–5.22 Gas Pressure Relationships (Pressure–Temperature and Pressure–Volume)- Study Notes- New syllabus
Edexcel iGCSE Physics -5.20–5.22 Gas Pressure Relationships (Pressure–Temperature and Pressure–Volume)- Study Notes -Edexcel iGCSE Physics – per latest Syllabus.
Key Concepts:
update
Gas Pressure Relationships (Fixed Amount of Gas)
For a fixed amount of gas, the pressure depends on how often and how forcefully gas molecules collide with the walls of the container. These collisions are affected by the volume and the Kelvin temperature of the gas.
Pressure and Volume at Constant Temperature
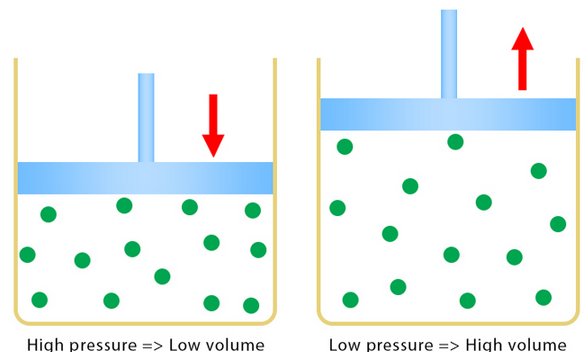
Qualitative relationship
- If the volume of a gas decreases, the pressure increases.
- If the volume of a gas increases, the pressure decreases.
- Temperature must remain constant.
This relationship is known as Boyle’s law.
Boyle’s law (statement)
For a fixed mass of gas at constant temperature, pressure is inversely proportional to volume.
\( \mathrm{P \propto \dfrac{1}{V}} \)
Particle Explanation
- Reducing volume brings the container walls closer together.
- Molecules collide with the walls more frequently.
- More collisions per second increases the force on the walls.
- This results in a higher pressure.
The average speed of the molecules stays the same because temperature is constant.
Pressure and Kelvin Temperature at Constant Volume
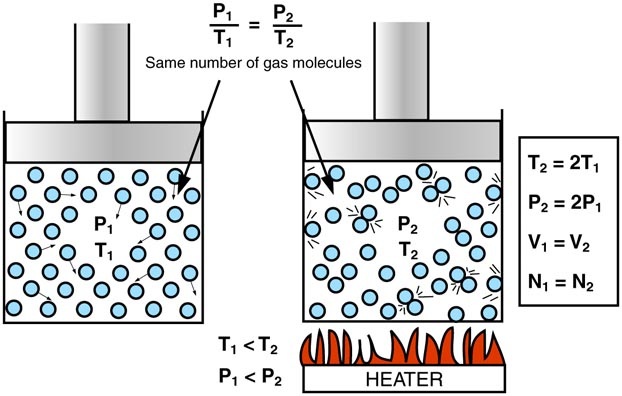
Qualitative relationship
- If the Kelvin temperature increases, the pressure increases.
- If the Kelvin temperature decreases, the pressure decreases.
- Volume must remain constant.
Pressure–temperature relationship
\( \mathrm{P \propto T} \) (when volume is constant)
Particle Explanation
- Increasing temperature increases the kinetic energy of molecules.
- Molecules move faster.
- Collisions with the walls are more frequent and more forceful.
- This increases the pressure.
Kelvin temperature must be used because it is proportional to kinetic energy.
Key Idea
- Pressure depends on molecular collisions.
- Volume affects collision frequency.
- Temperature affects collision energy.
Important Points to Remember
- Amount of gas must be constant.
- Temperature must be constant for Boyle’s law.
- Volume must be constant for pressure–temperature relationship.
- Always use Kelvin temperature.
Example
A gas is trapped in a sealed syringe at constant temperature.
The plunger is pushed in, reducing the volume.
Explain what happens to the pressure of the gas.
▶️ Answer / Explanation
Reducing the volume brings the walls closer together.
Gas molecules collide with the walls more frequently.
This increases the force on the walls, so the pressure increases.
Example
A fixed mass of gas is sealed in a rigid container.
The gas is heated.
Explain why the pressure increases.
▶️ Answer / Explanation
Heating increases the kinetic energy of the gas molecules.
The molecules move faster and collide with the walls more often and with greater force.
This increases the pressure.
Pressure–Temperature Relationship (Constant Volume)
For a fixed mass of gas kept at a constant volume, the pressure of the gas depends directly on its Kelvin temperature.
This relationship is sometimes called the pressure law.
The Pressure–Temperature Relationship
At constant volume:
Pressure is directly proportional to the Kelvin temperature
\( \mathrm{P \propto T} \)
This means:
\( \mathrm{\dfrac{P_1}{T_1} = \dfrac{P_2}{T_2}} \)
- \( \mathrm{P} \) = pressure (Pa)
- \( \mathrm{T} \) = temperature (K)
Important Condition
- The volume must remain constant.
- The mass of gas must be fixed.
- Temperature must be measured in kelvin, not °C.
Particle Explanation
- Heating the gas increases the kinetic energy of molecules.
- Molecules move faster.
- Collisions with the container walls are more frequent and more forceful.
- This increases the pressure.
If the Kelvin temperature doubles, the average kinetic energy doubles, so the pressure also doubles.
Graphical Representation
- A graph of pressure against Kelvin temperature is a straight line.
- The line passes through the origin (0 K, 0 Pa).
This shows that pressure would be zero at absolute zero.
Key Idea
- Pressure depends on molecular collisions.
- Higher Kelvin temperature → higher pressure.
- Kelvin temperature is essential.
Important Points to Remember
- Always convert °C to K before using the formula.
- Do not use this relationship if volume changes.
- This applies only to gases.
Example
A gas in a rigid container has a pressure of \( \mathrm{100\ kPa} \) at a temperature of \( \mathrm{300\ K} \).
Calculate the pressure when the temperature is increased to \( \mathrm{450\ K} \).
▶️ Answer / Explanation
Use:
\( \mathrm{\dfrac{P_1}{T_1} = \dfrac{P_2}{T_2}} \)
\( \mathrm{\dfrac{100}{300} = \dfrac{P_2}{450}} \)
\( \mathrm{P_2 = 150\ kPa} \)
Example
A gas at constant volume has a pressure of \( \mathrm{80\ kPa} \) at \( \mathrm{27^\circ C} \).
Calculate the pressure when the temperature is increased to \( \mathrm{127^\circ C} \).
▶️ Answer / Explanation
Convert to kelvin:
\( \mathrm{27^\circ C = 300\ K} \)
\( \mathrm{127^\circ C = 400\ K} \)
Use:
\( \mathrm{\dfrac{P_1}{T_1} = \dfrac{P_2}{T_2}} \)
\( \mathrm{\dfrac{80}{300} = \dfrac{P_2}{400}} \)
\( \mathrm{P_2 \approx 107\ kPa} \)
Pressure–Volume Relationship (Constant Temperature)
For a fixed mass of gas kept at a constant temperature, the pressure of the gas depends on the volume it occupies. This relationship is known as Boyle’s law.
Boyle’s Law
For a fixed mass of gas at constant temperature, pressure is inversely proportional to volume.
\( \mathrm{P \propto \dfrac{1}{V}} \)
This can also be written as:
\( \mathrm{P_1 V_1 = P_2 V_2} \)
- \( \mathrm{P} \) = pressure (Pa)
- \( \mathrm{V} \) = volume (m³)
Conditions Required
- The temperature must remain constant.
- The mass of gas must be fixed.
- This relationship applies only to gases.
Particle Explanation
- Gas pressure is caused by collisions of molecules with container walls.
- When volume decreases, the walls are closer together.
- Molecules collide with the walls more frequently.
- This increases the force on the walls and therefore the pressure.
The average speed of the molecules stays the same because temperature is constant.
Graphical Representation
- A graph of pressure against volume is a curve.
- A graph of pressure against \( \mathrm{\frac{1}{V}} \) is a straight line.
Key Idea
- Smaller volume → higher pressure.
- Larger volume → lower pressure.
- Boyle’s law links pressure and volume.
Important Points to Remember
- Do not apply Boyle’s law if temperature changes.
- Use consistent units for pressure and volume.
- This law is commonly tested using syringes or sealed tubes.
Example
A gas has a pressure of \( \mathrm{120\ kPa} \) and a volume of \( \mathrm{0.040\ m^3} \).
The gas is compressed at constant temperature to a volume of \( \mathrm{0.025\ m^3} \).
Calculate the new pressure.
▶️ Answer / Explanation
Use Boyle’s law:
\( \mathrm{P_1 V_1 = P_2 V_2} \)
\( \mathrm{120 \times 0.040 = P_2 \times 0.025} \)
\( \mathrm{P_2 = 192\ kPa} \)
Example
A gas in a syringe has a volume of \( \mathrm{60\ cm^3} \) at a pressure of \( \mathrm{100\ kPa} \).
The pressure is increased to \( \mathrm{150\ kPa} \) while the temperature remains constant.
Calculate the new volume of the gas.
▶️ Answer / Explanation
Use:
\( \mathrm{P_1 V_1 = P_2 V_2} \)
\( \mathrm{100 \times 60 = 150 \times V_2} \)
\( \mathrm{V_2 = 40\ cm^3} \)