Edexcel iGCSE Physics -5.4 Core Practical: Density Measurements- Study Notes- New Syllabus

Practical: Investigating Density Using Direct Measurements of Mass and Volume

Density can be found by measuring the mass and volume of an object directly and using the density equation.

Aim

To determine the density of a material by measuring its mass and volume.

Apparatus

• Electronic balance
• Measuring cylinder
• Solid object (regular or irregular)
• Water
• Ruler (for regular shapes)

Key Relationship Used

\( \mathrm{density = \dfrac{mass}{volume}} \)

\( \mathrm{\rho = \dfrac{m}{V}} \)

• Density in kg/m³
• Mass in kg
• Volume in m³

Method A: Regular Solid

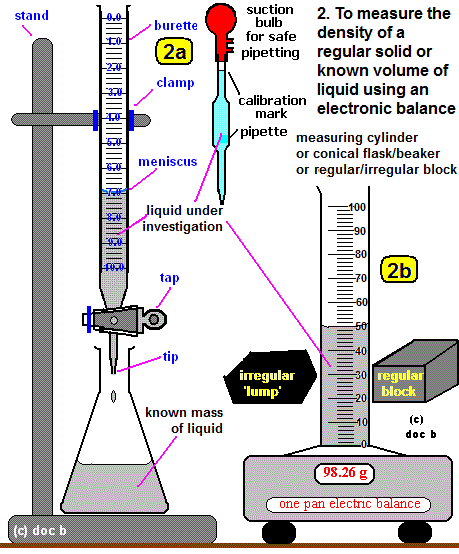
• Measure the mass of the object using the balance.
• Measure its dimensions using a ruler.
• Calculate the volume using the appropriate formula.
• Calculate density using \( \mathrm{\rho = m/V} \).

Example volume calculation:

\( \mathrm{volume\ of\ cuboid = length \times width \times height} \)

Method B: Irregular Solid (Displacement Method)

• Measure the mass of the object.
• Pour water into a measuring cylinder and record the initial volume.
• Lower the object fully into the water.
• Record the final volume.
• Volume of object = final volume − initial volume.
• Calculate density.

Variables

• Independent: object used
• Dependent: calculated density
• Controlled: same balance, same measuring cylinder, temperature

Conclusion

• Density depends on the material.
• Mass and volume measurements allow density to be calculated accurately.
• Objects of the same material have the same density.

Safety Precautions

• Handle glassware carefully.
• Dry objects before measuring mass.
• Prevent water spills near electrical equipment.

Sources of Error & Improvements

• Reading the meniscus incorrectly → read at eye level.
• Air bubbles on object → lower slowly.
• Use a balance with higher resolution.

Key Idea

• Density compares mass to volume.
• Displacement is used for irregular objects.
• SI units must be used.