Edexcel iGCSE Physics -5.5 Pressure, Force, and Area- Study Notes- New Syllabus

Pressure, Force and Area

Pressure describes how concentrated a force is over a surface. A large force acting on a small area produces a high pressure, while the same force acting over a larger area produces a lower pressure.

Relationship Between Pressure, Force and Area

The relationship is:

\( \mathrm{pressure = \dfrac{force}{area}} \)

\( \mathrm{P = \dfrac{F}{A}} \)

• \( \mathrm{P} \) = pressure (pascal, Pa)
• \( \mathrm{F} \) = force (newton, N)
• \( \mathrm{A} \) = area (square metre, m²)

1 pascal = 1 newton per square metre (N/m²).

Understanding the Relationship

• For a constant force, decreasing the area increases pressure.
• For a constant area, increasing the force increases pressure.
• Pressure depends on both force and contact area.

Everyday examples:

• Sharp knives cut better because they have a small contact area.
• High-heeled shoes exert more pressure than flat shoes.
• Snowshoes reduce pressure to prevent sinking into snow.

Rearranging the Formula

• Force: \( \mathrm{F = P \times A} \)
• Area: \( \mathrm{A = \dfrac{F}{P}} \)

Key Idea

• Pressure is force per unit area.
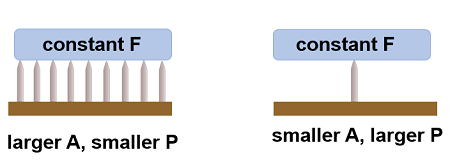
• Small area → high pressure.
• Large area → low pressure.

Important Points to Remember

• Area must be in m².
• Force must be in newtons.
• Pressure is measured in pascals.