Edexcel iGCSE Physics -5.6–5.7 Pressure in Fluids at Rest and Pressure Difference- Study Notes- New Syllabus
Edexcel iGCSE Physics -5.6–5.7 Pressure in Fluids at Rest and Pressure Difference- Study Notes- New syllabus
Edexcel iGCSE Physics -5.6–5.7 Pressure in Fluids at Rest and Pressure Difference- Study Notes -Edexcel iGCSE Physics – per latest Syllabus.
Key Concepts:
update
Pressure in Fluids Acts Equally in All Directions
In a fluid at rest (a liquid or a gas), the pressure at a point acts equally in all directions. This means the force due to pressure pushes sideways, upwards, and downwards with the same strength at the same depth.
Key Idea
- Pressure in a fluid acts perpendicular to any surface.
- At a given point, pressure is the same in all directions.
- This is true only when the fluid is at rest.
Why Pressure Acts in All Directions
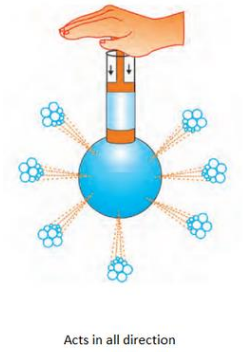
- Fluid particles move randomly.
- They collide with surfaces from all directions.
- These collisions produce pressure equally in every direction.
This explains why containers holding liquids or gases must be strong on all sides.
Pressure in Liquids
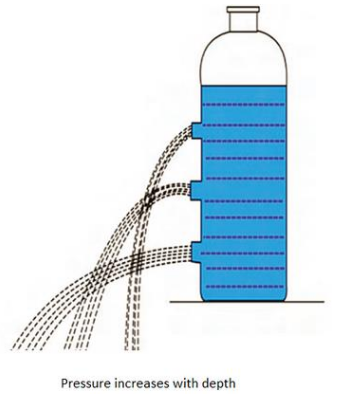
- Pressure increases with depth.
- At the same depth, pressure is the same in all directions.
- Pressure pushes sideways on walls and upwards on objects.
Example: Water pushes equally on all sides of a submerged object.
Pressure in Gases

- Gas pressure acts on the walls of a container.
- Pressure acts equally in all directions.
- Increasing temperature increases gas pressure.
Example: Air inside a balloon pushes equally on all sides, keeping it spherical.
Link to Pressure Formula
Pressure is defined as:
\( \mathrm{P = \dfrac{F}{A}} \)
Because pressure acts equally in all directions, the force on a surface depends on:
- The pressure at that point
- The area of the surface
Applications of Equal Pressure
- Hydraulic systems (brakes, lifts)
- Dams designed thicker at the bottom
- Diving and submarine design
Important Points to Remember
- Pressure acts equally in all directions at a point.
- It always acts perpendicular to a surface.
- This applies to both liquids and gases at rest.
Example
A small cube is completely submerged in water at a fixed depth.
Explain why the water exerts forces on all sides of the cube.
▶️ Answer / Explanation
Water pressure at a point acts equally in all directions.
At the same depth, the pressure is the same on every side of the cube.
This causes forces to act on all faces of the cube.
Example
A balloon is filled with air and sealed.
Explain why the balloon expands equally in all directions.
▶️ Answer / Explanation
Air pressure inside the balloon acts equally in all directions.
The pressure pushes outward on the balloon’s surface everywhere.
This causes the balloon to expand uniformly.
Pressure Difference in Liquids
In a liquid at rest, the pressure increases with depth. This is because the deeper you go, the more liquid there is above you, and therefore the greater the weight of liquid acting downwards.
The pressure difference between two points in a liquid depends only on the vertical height difference, the density of the liquid, and the gravitational field strength.
Relationship for Pressure Difference
The pressure difference between two points in a liquid is given by:
\( \mathrm{pressure\ difference = height \times density \times gravitational\ field\ strength} \)
\( \mathrm{\Delta P = h \rho g} \)
- \( \mathrm{\Delta P} \) = pressure difference (pascal, Pa)
- \( \mathrm{h} \) = vertical height difference (metre, m)
- \( \mathrm{\rho} \) = density of the liquid (kg/m³)
- \( \mathrm{g} \) = gravitational field strength (N/kg)
Understanding the Relationship
- Greater depth → larger pressure difference.
- Denser liquids produce greater pressure.
- Pressure difference depends on vertical height, not container shape.
This explains why dams are thicker at the bottom and why divers feel more pressure at greater depths.
Important Points to Remember
- The liquid must be at rest.
- Height is measured vertically.
- Pressure difference is independent of surface area.
Key Idea
- Pressure increases with depth in a liquid.
- Same depth → same pressure in all directions.
- Only density, height, and gravity matter.
Applications
- Design of dams and submarines
- Diving and underwater safety
- Water supply systems
Example
Calculate the pressure difference between the surface and a point \( \mathrm{5.0\ m} \) below the surface of water.
(Density of water \( \mathrm{= 1000\ kg/m^3} \), \( \mathrm{g = 10\ N/kg} \))
▶️ Answer / Explanation
Use:
\( \mathrm{\Delta P = h \rho g} \)
\( \mathrm{\Delta P = 5.0 \times 1000 \times 10} \)
\( \mathrm{\Delta P = 50\,000\ Pa} \)
Example
A liquid has a density of \( \mathrm{800\ kg/m^3} \).
The pressure difference between two points in the liquid is \( \mathrm{12\,000\ Pa} \).
Calculate the vertical height difference between the two points.
(Take \( \mathrm{g = 10\ N/kg} \))
▶️ Answer / Explanation
Rearrange:
\( \mathrm{h = \dfrac{\Delta P}{\rho g}} \)
\( \mathrm{h = \dfrac{12\,000}{800 \times 10}} \)
\( \mathrm{h = 1.5\ m} \)
