Edexcel iGCSE Physics -8.15–8.16P Red-Shift, Motion of Galaxies, the Red-Shift Equation- Study Notes- New Syllabus
Edexcel iGCSE Physics -8.15–8.16P Red-Shift, Motion of Galaxies, the Red-Shift Equation- Study Notes- New syllabus
Edexcel iGCSE Physics -8.15–8.16P Red-Shift, Motion of Galaxies, the Red-Shift Equation- Study Notes -Edexcel iGCSE Physics – per latest Syllabus.
Key Concepts:
update
Effect of Relative Motion on Observed Frequency and Wavelength (Doppler Effect)
When a wave source moves relative to an observer, the observed frequency and wavelength of the wave change. This phenomenon is known as the Doppler effect.
Key Statement
Statement: If a wave source is moving relative to an observer, the observed frequency and wavelength of the wave will change.
Key idea: Relative motion causes wavefronts to be compressed or spread out.
What Is the Doppler Effect?
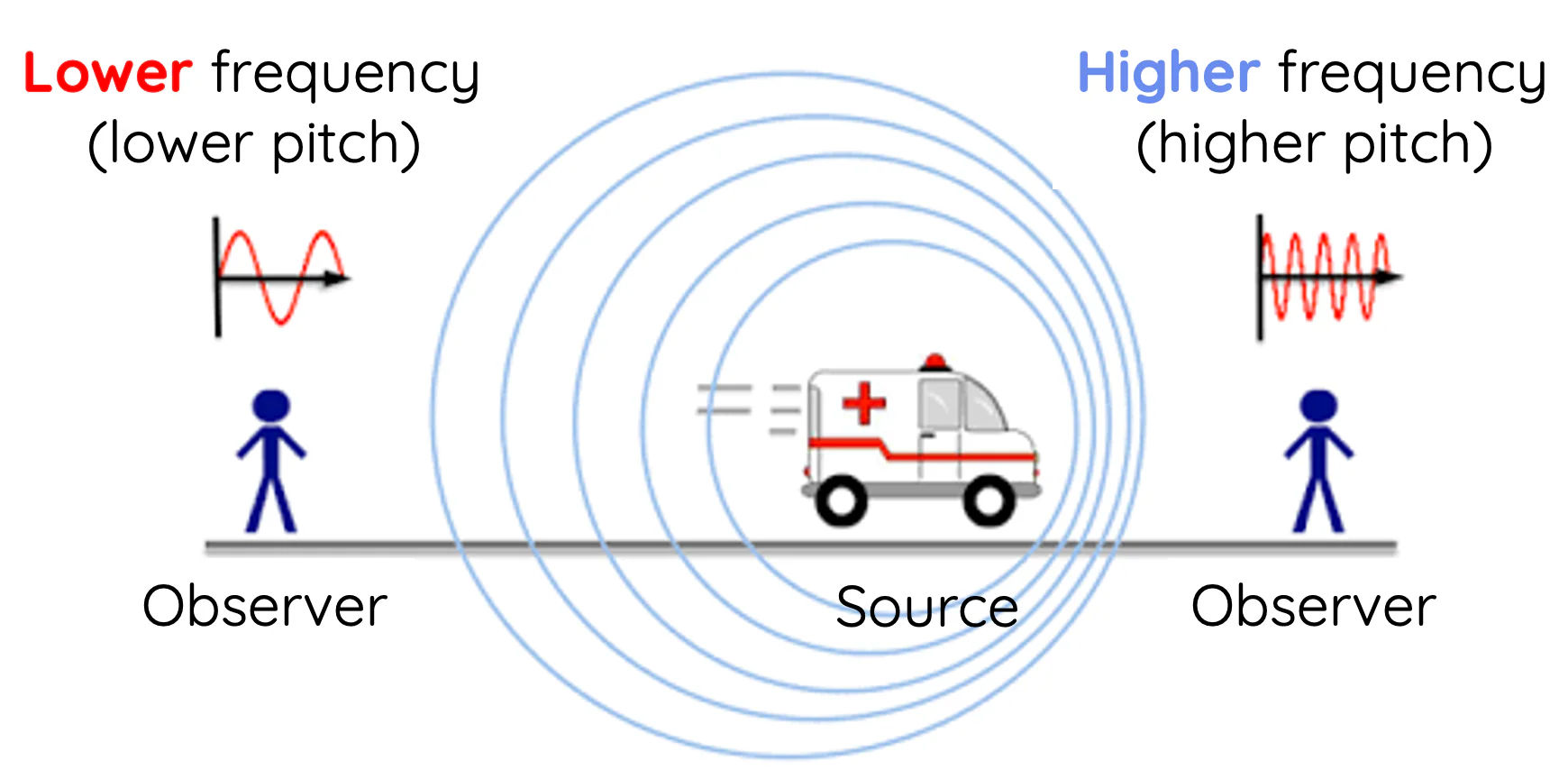
- It occurs when there is relative motion between source and observer.
- It applies to all types of waves.
- It changes the observed frequency and wavelength.
Important: The wave speed in the medium remains constant.
Source Moving Towards the Observer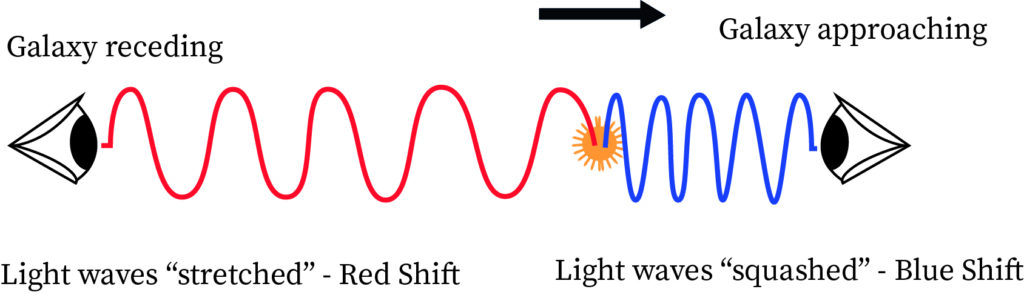
- Wavefronts are compressed.
- Wavelength decreases.
- Observed frequency increases.
Result: The observer detects a higher frequency than emitted.
Source Moving Away from the Observer
- Wavefronts are spread out.
- Wavelength increases.
- Observed frequency decreases.
Result: The observer detects a lower frequency than emitted.
Why Frequency Changes
- The source emits waves at a constant rate.
- Movement changes spacing between wavefronts.
- This changes wavelength.
Key relationship:
\( \mathrm{v = f\lambda} \)
- Wave speed \( \mathrm{v} \) stays constant.
- If \( \mathrm{\lambda} \) decreases, \( \mathrm{f} \) must increase.
- If \( \mathrm{\lambda} \) increases, \( \mathrm{f} \) must decrease.
Doppler Effect in Light Waves
- Light from moving objects changes frequency.
- Moving away → red shift.
- Moving towards → blue shift.
Key idea: This effect is used in astronomy to study motion of stars and galaxies.
Example
A sound source moves towards a stationary observer. Explain how the observed frequency and wavelength change and why.
▶️ Answer / Explanation
- The source moves toward the observer.
- Wavefronts are compressed.
- The wavelength decreases.
- The wave speed stays constant.
- The observed frequency increases.
Example
Light from a distant galaxy is observed to be red-shifted. Explain what this indicates about the motion of the galaxy and how the Doppler effect causes this change.
▶️ Answer / Explanation
- Red shift means the wavelength has increased.
- This indicates the galaxy is moving away.
- Wavefronts are spread out due to motion.
- The observed frequency decreases.
- This is caused by the Doppler effect.
Using the Red-Shift Equation for Galaxies
Light from distant galaxies shows a change in wavelength due to their motion relative to Earth. This effect allows astronomers to calculate the velocity of a galaxy using the red-shift equation.
Key Statement
Statement: The velocity of a galaxy moving away from Earth can be found using the relationship between the change in wavelength, the reference wavelength, and the speed of light.
Key idea: A larger change in wavelength corresponds to a greater recessional speed.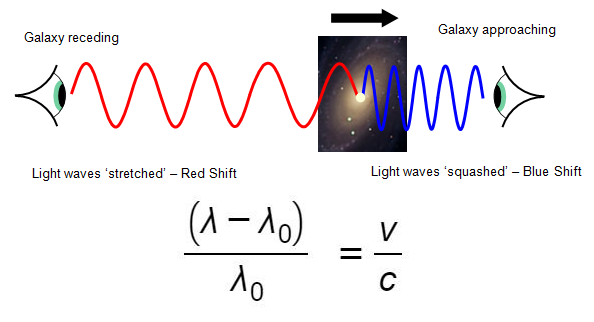
The Red-Shift Relationship
Written in words:
(change in wavelength) ÷ (reference wavelength) = (velocity of galaxy) ÷ (speed of light)
Mathematically:
\( \mathrm{\dfrac{\lambda – \lambda_0}{\lambda_0} = \dfrac{\Delta \lambda}{\lambda_0} = \dfrac{v}{c}} \)
- \( \mathrm{\lambda} \) = observed wavelength (m)
- \( \mathrm{\lambda_0} \) = reference (original) wavelength (m)
- \( \mathrm{\Delta \lambda} \) = change in wavelength (m)
- \( \mathrm{v} \) = velocity of the galaxy (m/s)
- \( \mathrm{c} \) = speed of light (\( \mathrm{3.0 \times 10^8\ m/s} \))
Meaning of the Equation
- The reference wavelength is measured in a laboratory on Earth.
- The observed wavelength is measured from the galaxy.
- If \( \mathrm{\lambda > \lambda_0} \), the wavelength has increased.
- An increase in wavelength indicates red shift.
Key idea: Red shift means the galaxy is moving away from Earth.
Rearranged Forms Used in Exams
- To calculate galaxy velocity:
\( \mathrm{v = \dfrac{\Delta \lambda}{\lambda_0} \times c} \)
- To calculate change in wavelength:
\( \mathrm{\Delta \lambda = \dfrac{v}{c} \times \lambda_0} \)
Important Exam Conditions
- Valid when galaxy speed is much less than the speed of light.
- All wavelengths must be in the same units.
- Usually applied to galaxies moving directly away from Earth.
Common Exam Errors
- Using observed wavelength instead of reference wavelength in the denominator.
- Forgetting to convert nm to m.
- Using \( \mathrm{\lambda} \) instead of \( \mathrm{\Delta \lambda} \).
Example
A spectral line has a reference wavelength of \( \mathrm{480\ nm} \). The same line is observed from a distant galaxy at \( \mathrm{492\ nm} \). Calculate the velocity of the galaxy.
▶️ Answer / Explanation
Change in wavelength:
\( \mathrm{\Delta \lambda = 492 – 480 = 12\ nm = 1.2 \times 10^{-8}\ m} \)
Reference wavelength:
\( \mathrm{\lambda_0 = 480\ nm = 4.8 \times 10^{-7}\ m} \)
Using:
\( \mathrm{v = \dfrac{\Delta \lambda}{\lambda_0} \times c} \)
\( \mathrm{v = \dfrac{1.2 \times 10^{-8}}{4.8 \times 10^{-7}} \times 3.0 \times 10^8} \)
\( \mathrm{v = 7.5 \times 10^6\ m/s} \)
Galaxy velocity = \( \mathrm{7.5 \times 10^6\ m/s} \)
Example
A galaxy is moving away from Earth at \( \mathrm{1.5 \times 10^7\ m/s} \). A spectral line has a reference wavelength of \( \mathrm{600\ nm} \). Calculate the observed wavelength.
▶️ Answer / Explanation
Using:
\( \mathrm{\Delta \lambda = \dfrac{v}{c} \times \lambda_0} \)
\( \mathrm{\Delta \lambda = \dfrac{1.5 \times 10^7}{3.0 \times 10^8} \times 600 \times 10^{-9}} \)
\( \mathrm{\Delta \lambda = 3.0 \times 10^{-8}\ m = 30\ nm} \)
Observed wavelength:
\( \mathrm{\lambda = \lambda_0 + \Delta \lambda = 600 + 30 = 630\ nm} \)
Observed wavelength = \( \mathrm{630\ nm} \)