Edexcel iGCSE Physics -8.6 Orbital Speed, Radius, and Time Period- Study Notes- New Syllabus
Edexcel iGCSE Physics -8.6 Orbital Speed, Radius, and Time Period- Study Notes- New syllabus
Edexcel iGCSE Physics -8.6 Orbital Speed, Radius, and Time Period- Study Notes -Edexcel iGCSE Physics – per latest Syllabus.
Key Concepts:
update
Orbital Speed, Orbital Radius and Time Period
Objects such as planets, moons, and artificial satellites move in circular or near-circular orbits. Their motion can be described using the relationship between orbital speed, orbital radius, and time period.
Key Statement
Statement: The orbital speed of an object depends on the radius of its orbit and the time period of the orbit.
Key idea: In one complete orbit, the object travels one circumference.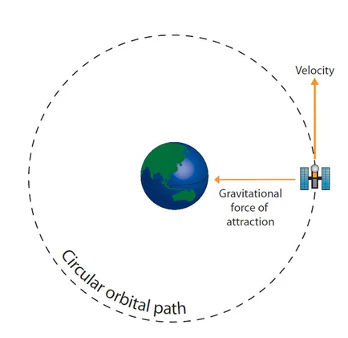
The Orbital Speed Relationship
Formula:
\( \mathrm{v = \dfrac{2\pi r}{T}} \)
- \( \mathrm{v} \) = orbital speed (m/s)
- \( \mathrm{r} \) = orbital radius (m)
- \( \mathrm{T} \) = time period (s)
Explanation:
- The distance travelled in one orbit is \( \mathrm{2\pi r} \).
- The time taken for one orbit is \( \mathrm{T} \).
- Speed = distance ÷ time.
Understanding the Relationship
- Larger orbital radius → larger distance per orbit.
- Shorter time period → higher orbital speed.
- For circular orbits, speed is constant in magnitude.
Key idea: Changing either the radius or the time period changes the orbital speed.
Rearranging the Formula
- To find radius:
\( \mathrm{r = \dfrac{vT}{2\pi}} \)
- To find time period:
\( \mathrm{T = \dfrac{2\pi r}{v}} \)
Common Exam Pitfalls
- Forgetting to convert time into seconds.
- Using diameter instead of radius.
- Omitting \( \mathrm{2\pi} \).
Example
An artificial satellite moves in a circular orbit of radius \( \mathrm{7.0 \times 10^6\ m} \) around the Earth. The time period of the orbit is 6000 s. Calculate the orbital speed of the satellite.
▶️ Answer / Explanation
Using:
\( \mathrm{v = \dfrac{2\pi r}{T}} \)
\( \mathrm{v = \dfrac{2\pi \times 7.0 \times 10^6}{6000}} \)
\( \mathrm{v \approx 7.3 \times 10^3\ m/s} \)
Orbital speed ≈ 7300 m/s
Example
A moon orbits a planet with a constant orbital speed of \( \mathrm{1.8 \times 10^3\ m/s} \). The orbital radius is \( \mathrm{4.0 \times 10^7\ m} \). Calculate the time period of the orbit.
▶️ Answer / Explanation
Using:
\( \mathrm{T = \dfrac{2\pi r}{v}} \)
\( \mathrm{T = \dfrac{2\pi \times 4.0 \times 10^7}{1.8 \times 10^3}} \)
\( \mathrm{T \approx 1.4 \times 10^5\ s} \)
Time period ≈ \( \mathrm{1.4 \times 10^5\ s} \)