Edexcel iGCSE Physics -4.3 Conservation of Energy- Study Notes- New Syllabus

Principle of Conservation of Energy

The principle of conservation of energy states that energy cannot be created or destroyed. It can only be transferred from one energy store to another.

This principle applies to all physical processes and is used to analyse motion, heating, electrical devices, and energy systems.

Statement of the Principle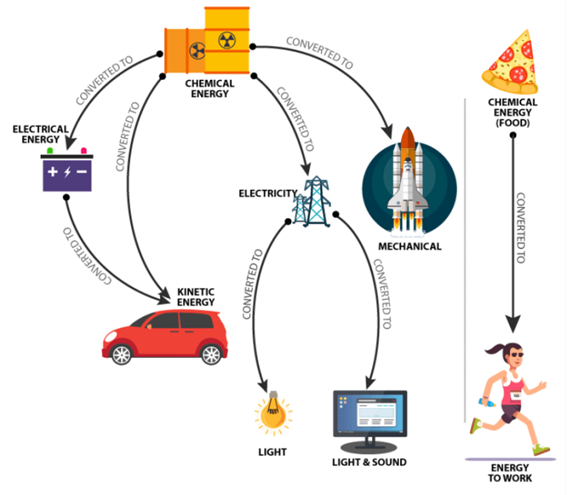

• The total energy of a closed system remains constant.
• Energy is not lost — it is only transferred to different stores.
• Any energy that appears “wasted” is usually transferred to the thermal store of the surroundings.

Energy Transfers and Stores

When energy changes form, it moves between energy stores:

• Chemical → kinetic
• Gravitational → kinetic
• Elastic → kinetic
• Electrical → thermal / light / sound

The total energy before the transfer equals the total energy after the transfer.

Using Conservation of Energy in Calculations

In an ideal system (no energy losses):

Energy before = Energy after

For example:

• Gravitational potential energy = kinetic energy

\( \mathrm{mgh = \dfrac{1}{2}mv^2} \)

Mass often cancels out, simplifying calculations.

Real Systems

• Some energy is transferred to the thermal store due to friction.
• Some energy may be transferred as sound or light.
• Total energy is still conserved.

Sankey diagrams are often used to show these energy transfers.

Key Idea

• Energy before = energy after.
• Energy is transferred, not destroyed.
• Useful and wasted energy together equal total energy input.

Important Points to Remember

• Always identify energy stores clearly.
• Use correct energy equations.
• Include all energy transfers, including thermal losses.