Edexcel A Level (IAL) Physics-1.1 Equations of Motion- Study Notes- New Syllabus
Edexcel A Level (IAL) Physics -1.1 Equations of Motion- Study Notes- New syllabus
Edexcel A Level (IAL) Physics -1.1 Equations of Motion- Study Notes -Edexcel A level Physics – per latest Syllabus.
Key Concepts:
- 1.1 be able to use the equations for uniformly accelerated motion in one dimension:
$s = \frac{(u + v)t}{2}$
$v = u + at$
$s = ut + \frac{1}{2}at^2$
$v^2 = u^2 + 2as$
Equations of Uniformly Accelerated Motion (SUVAT)
When an object moves in a straight line with constant acceleration, its motion can be described using the SUVAT equations.
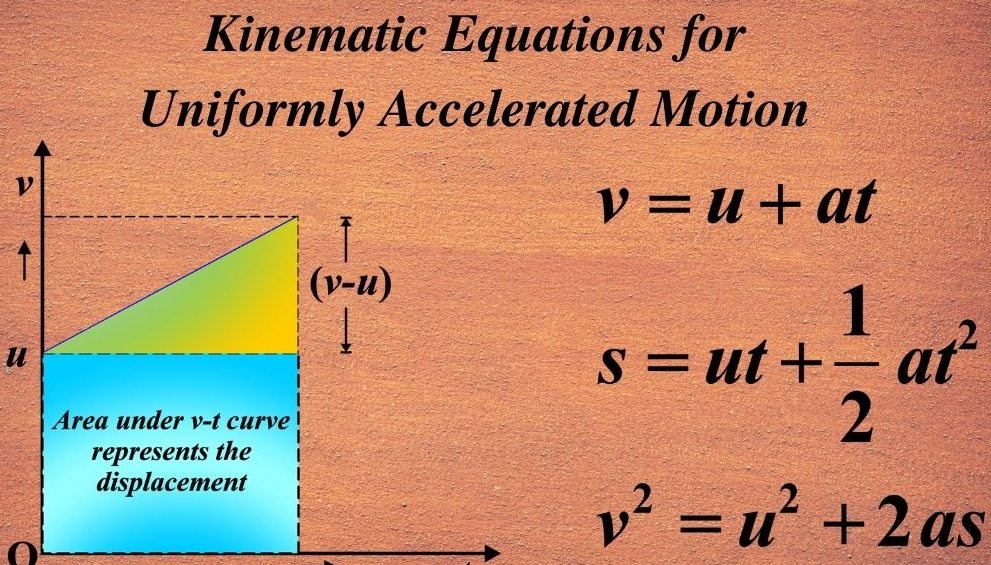
\( \mathrm{s = \dfrac{(u + v)t}{2}} \)
\( \mathrm{v = u + at} \)
\( \mathrm{s = ut + \dfrac{1}{2}at^2} \)
\( \mathrm{v^2 = u^2 + 2as} \)
- \( \mathrm{u} \) = initial velocity (m s⁻¹)
- \( \mathrm{v} \) = final velocity (m s⁻¹)
- \( \mathrm{a} \) = constant acceleration (m s⁻²)
- \( \mathrm{s} \) = displacement (m)
- \( \mathrm{t} \) = time (s)
Key Meaning of the SUVAT Equations:
- They apply only when acceleration is constant.
- If any 3 quantities among \( \mathrm{s, u, v, a, t} \) are known, the rest can be found.
- They describe linear motion in one dimension.
Understanding Each Equation
- \( \mathrm{s = \dfrac{(u+v)t}{2}} \): distance = average velocity × time.
- \( \mathrm{v = u + at} \): definition of constant acceleration.
- \( \mathrm{s = ut + \dfrac{1}{2}at^2} \): displacement after accelerating from velocity \( \mathrm{u} \).
- \( \mathrm{v^2 = u^2 + 2as} \): useful when time is not known.
Example (Easy)
A car starts from rest and accelerates at \( \mathrm{2\,m\,s^{-2}} \) for \( \mathrm{5\,s} \). Find its final velocity.
▶️ Answer / Explanation
Use: \( \mathrm{v = u + at} \)
\( \mathrm{v = 0 + (2)(5)} \)
\( \mathrm{v = 10\,m\,s^{-1}} \)
Example (Medium)
A cyclist slows from \( \mathrm{20\,m\,s^{-1}} \) to \( \mathrm{10\,m\,s^{-1}} \) in \( \mathrm{4\,s} \). Find the acceleration and distance travelled during this time.
▶️ Answer / Explanation
Step 1: Acceleration
\( \mathrm{10 = 20 + a(4)} \)
\( \mathrm{a = -2.5\,m\,s^{-2}} \)
Step 2: Distance
\( \mathrm{s = \dfrac{(u+v)t}{2}} \)
\( \mathrm{s = \dfrac{(20 + 10)4}{2} = 60\,m} \)
Example (Hard)
A particle has initial velocity \( \mathrm{12\,m\,s^{-1}} \) and acceleration \( \mathrm{-3\,m\,s^{-2}} \). Find the time taken to stop and the distance travelled before coming to rest.
▶️ Answer / Explanation
Step 1: Time to stop
\( \mathrm{0 = 12 – 3t} \)
\( \mathrm{t = 4\,s} \)
Step 2: Distance travelled
\( \mathrm{s = ut + \dfrac{1}{2}at^2} \)
\( \mathrm{s = 12(4) + \dfrac{1}{2}(-3)(4^2)} \)
\( \mathrm{s = 48 – 24 = 24\,m} \)
