Edexcel A Level (IAL) Physics-1.11 Core Practical 1: Investigating the Acceleration of Freefall- Study Notes- New Syllabus

CORE PRACTICAL 1: Determine the Acceleration of a Freely-Falling Object

This core practical aims to measure the acceleration due to gravity \( g \) by analysing the motion of an object falling freely under gravity.

 Aim of the Experiment

To determine the value of gravitational acceleration \( g \) using the equation of motion:

\( s = ut + \dfrac{1}{2}gt^2 \)

For a freely falling object: \( u = 0 \) → initial velocity is zero.

Apparatus

• Light gate(s)
• Electronic timer
• Data logger (optional)
• Clamp stand
• Ball bearing (or similar small dense object)
• Metre ruler

 Method (Using One Light Gate)

• Set up a light gate connected to an electronic timer.
• Measure the height \( h \) from the bottom of the ball to the top of the light gate.
• Hold the ball at the measured height and release it so it falls freely.
• The light gate measures the time \( t \) it takes for the ball to fall through the gate.
• Repeat several times for the same height, then for different heights.

Using the equation:

\( h = \dfrac{1}{2}gt^2 \)

Rearrange to find \( g \):

\( g = \dfrac{2h}{t^2} \)

 Alternative Method (Using Two Light Gates)

• Place two light gates a known distance \( s \) apart.
• As the object falls, each gate records its velocity at that point.
• The average acceleration is calculated using:

\( g = \dfrac{v_2 – v_1}{t} \)

Where:

• \( v_1 \) = velocity at first gate
• \( v_2 \) = velocity at second gate
• \( t \) = time between passing the two gates

 Data Processing

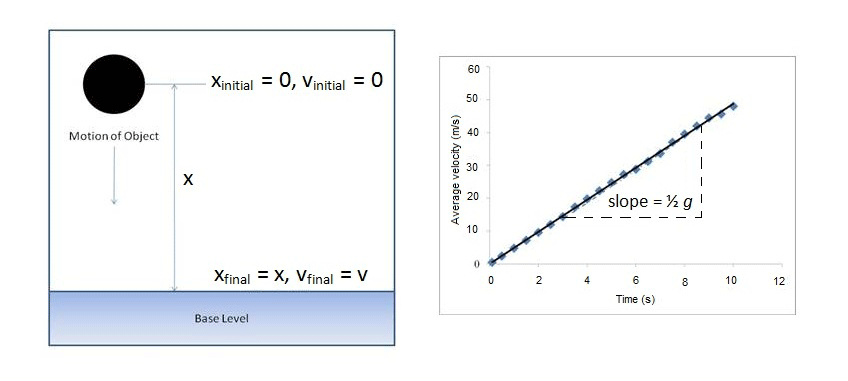
• Record several values of height and corresponding time.
• Plot a graph of \( h \) against \( t^2 \).
• The gradient of the straight line is \( \dfrac{1}{2}g \).
• Multiply the gradient by 2 to obtain \( g \).

Sources of Error

• Reaction time error if using manual timing (avoid by using light gates).
• Air resistance slowing the object slightly.
• Height measurement inaccuracies.
• The ball may not fall straight if released inconsistently.

 Improvements

• Use light gates instead of a stopwatch.
• Use a dense object (reduces air resistance effect).
• Ensure the ball is released without any initial push.
• Take multiple readings for each height and average them.