Edexcel A Level (IAL) Physics-1.16 Centre of Gravity & The Principle of Moments- Study Notes- New Syllabus
Edexcel A Level (IAL) Physics -1.16 Centre of Gravity & The Principle of Moments- Study Notes- New syllabus
Edexcel A Level (IAL) Physics -1.16 Centre of Gravity & The Principle of Moments- Study Notes -Edexcel A level Physics – per latest Syllabus.
Key Concepts:
- 1.16 be able to use the concept of centre of gravity of an extended body and apply the principle of moments to an extended body in equilibrium
Centre of Gravity and Applying the Principle of Moments to an Extended Body
Centre of Gravity (CoG)
The centre of gravity of an extended body is the point at which the entire weight of the body may be considered to act.
![]()
- It is the average location of the weight distribution.
- For symmetrical objects of uniform density, CoG lies at the geometric centre.
- If the shape or density is uneven, CoG is located closer to the heavier part.
- An object will topple if its vertical line of action of weight falls outside the base.
Practical Ways to Find the Centre of Gravity
![]()
- For a flat lamina: suspend the lamina from different points and draw vertical lines; CoG is where the lines intersect.
- For regular solids: use symmetry (e.g., midpoint, centre).
Principle of Moments
An extended body is in rotational equilibrium when the total clockwise moment about any point equals the total anticlockwise moment.
![]()
\(\text{Total clockwise moments} = \text{Total anticlockwise moments}\)
This principle allows us to solve problems involving beams, seesaws, levers, and other rotating systems.
- Moments must be taken about the same pivot point.
- Distances must be perpendicular distances.
- Forces acting through the pivot produce zero moment.
- Objects in equilibrium have no net force and no net moment.
Centre of Gravity in Moment Calculations
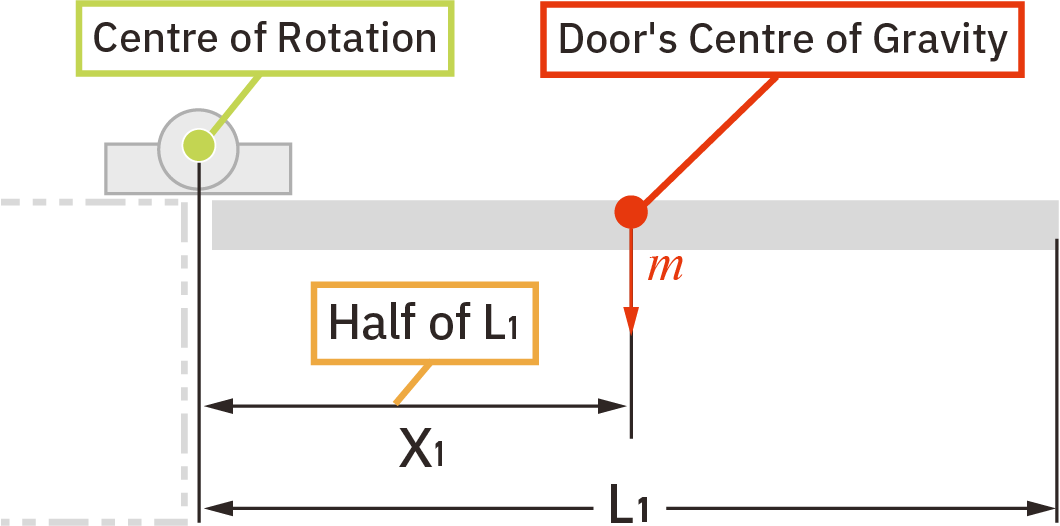
- The weight \( W = mg \) of an extended body acts at its centre of gravity.
- This weight produces a moment if the centre of gravity is not directly above the pivot.
- To balance a beam, the moment due to the object’s weight must be counteracted by other forces.
Applying Principle of Moments to an Extended Body in Equilibrium
For equilibrium:
\( \sum \text{Clockwise moments} = \sum \text{Anticlockwise moments} \)
- Use perpendicular distances only.
- Choose a pivot point that simplifies calculations (e.g., remove an unknown force).
- Replace the distributed weight of a body by a single weight acting at its CoG.
Example (Easy)
A uniform beam of length \( 2.0\, \mathrm{m} \) and weight \( 40\, \mathrm{N} \) is supported at one end. Find the moment of its weight about the support.
▶️ Answer / Explanation
The centre of gravity of a uniform beam is at its midpoint: \( 1.0\, \mathrm{m} \) from the support.
\( \text{Moment} = F x = 40 \times 1.0 = 40\, \mathrm{N\,m} \)
Example (Medium)
A non-uniform rod has its centre of gravity at \( 0.7\, \mathrm{m} \) from the left end. A \( 30\, \mathrm{N} \) weight acts downward at the right end. The rod balances horizontally when supported at a point \( 0.5\, \mathrm{m} \) from the left end. If the rod’s weight is \( 20\, \mathrm{N} \), find the weight at the right end.
▶️ Answer / Explanation
Take moments about the support point.
Rod’s weight produces an anticlockwise moment:
\( 20 \times (0.7 – 0.5) = 20 \times 0.2 = 4\, \mathrm{N\,m} \)
Let the right-end weight be \( W \).
Clockwise moment: \( W \times (1.0 – 0.5) = W \times 0.5 \)
Equating moments:
\( W \times 0.5 = 4 \Rightarrow W = 8\, \mathrm{N} \)
Example (Hard)
A \( 3.0\, \mathrm{m} \) uniform beam of weight \( 60\, \mathrm{N} \) rests horizontally on two supports. The left support is at the end of the beam, and the right support is \( 2.0\, \mathrm{m} \) from the left end. A \( 50\, \mathrm{N} \) load is placed \( 2.8\, \mathrm{m} \) from the left end. Find the reaction forces at each support.
▶️ Answer / Explanation
Take moments about the left support.
Beam’s weight acts at its centre: \( 1.5\, \mathrm{m} \) from the left.
Anticlockwise moments: \( 60 \times 1.5 = 90\, \mathrm{N\,m} \) (beam)
\( 50 \times 2.8 = 140\, \mathrm{N\,m} \) (load)
Total ACW moment = \( 230\, \mathrm{N\,m} \).
Clockwise moment provided by right support reaction \( R_2 \):
\( R_2 \times 2.0 = 230 \Rightarrow R_2 = 115\, \mathrm{N} \)
Total downward force = \( 60 + 50 = 110\, \mathrm{N} \)
Left support reaction:
\( R_1 = 110 – 115 = -5\, \mathrm{N} \)
A negative sign means the left support must actually pull down → in reality the beam lifts off the left support. So the right support takes all the load.
