Edexcel A Level (IAL) Physics-1.20 The Principle of Conservation of Energy- Study Notes- New Syllabus

Principle of Conservation of Energy

Principle of Conservation of Energy

Energy cannot be created or destroyed — it can only be transferred from one form to another. In a closed system, the total energy remains constant.

\(\text{Total Energy Initially} = \text{Total Energy Finally}\)

In mechanics, the main forms of energy we use are:

• Kinetic energy \( E_k = \tfrac{1}{2}mv^2 \)
• Gravitational potential energy \( E_{\text{grav}} = mg\Delta h \)
• Work done by forces \( W = F\Delta s \)

Energy Transfers Involving Work, GPE, and KE

• Work done on an object increases its energy.
• Work done by an object decreases its energy.
• Falling objects lose GPE and gain KE.
• Raising objects increases GPE and requires work to be done.
• If no energy is lost to friction,
  
  • \(\Delta E_k = -\Delta E_{\text{grav}}\)
  • \(\Delta E_{\text{grav}} + \Delta E_k + W_{\text{external}} = 0\)
• In real situations, some energy becomes thermal energy (not recoverable as mechanical energy).

Using Conservation of Energy in Calculations

For a system where only GPE and KE are involved (no friction):

\( mg\Delta h + \tfrac{1}{2}mu^2 = \tfrac{1}{2}mv^2 \)

With external work:

\( W_{\text{external}} + \text{Initial Energy} = \text{Final Energy} \)

With friction:

\( \text{Useful Energy Output} = \text{Energy Input} – \text{Work Against Friction} \)

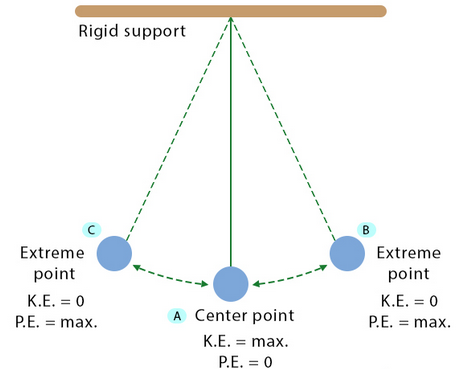
Energy Diagrams 

• At top of a fall: maximum GPE, minimum KE.
• At bottom of a fall: maximum KE, minimum GPE.
• Total mechanical energy remains (approximately) constant.