Edexcel A Level (IAL) Physics-1.25 Viscous Drag- Study Notes- New Syllabus
Edexcel A Level (IAL) Physics -1.25 Viscous Drag- Study Notes- New syllabus
Edexcel A Level (IAL) Physics -1.25 Viscous Drag- Study Notes -Edexcel A level Physics – per latest Syllabus.
Key Concepts:
- 1.25 a) be able to use the equation for viscous drag (Stokes’ Law), F = 6πηrv.
b) understand that this equation applies only to small spherical objects moving at low speeds with laminar flow (or in the absence of turbulent flow) and that viscosity is temperature dependent
Stokes’ Law \( F = 6\pi \eta r v \), Applicability & Temperature Dependence of Viscosity
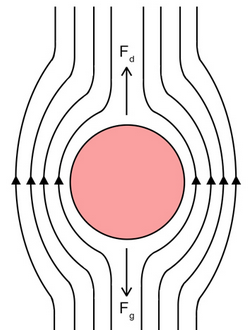
Stokes’ Law
When a small sphere moves slowly through a viscous fluid, it experiences a resistive force (viscous drag) opposing its motion.
The drag force is given by:
\( F = 6\pi \eta r v \)
- \( F \) = viscous drag force (N)
- \( \eta \) = coefficient of viscosity of the fluid (Pa·s)
- \( r \) = radius of the sphere (m)
- \( v \) = velocity of the sphere (m s⁻¹)
Understanding Stokes’ Law
- The force increases with velocity → faster motion produces more drag.
- The force is proportional to radius \( r \): larger objects experience more resistance.
- More viscous fluids (higher \( \eta \)) produce greater drag.
- Drag acts opposite to direction of motion (a resistive force).
Conditions for Stokes’ Law to Apply
Stokes’ Law is valid only under specific conditions:

- Object must be spherical — applies to small round objects (e.g., oil droplets, ball bearings).
- Flow must be laminar — smooth, layered flow with no turbulence.
- Velocity must be low — slow motion ensures no eddies are formed.
- Object must be small — so that the fluid flow stays smooth around it.
- The Reynolds number must be very small — typically \( \text{Re} \ll 1 \).
- No slip condition — fluid at the surface of the sphere has zero relative velocity.
If these conditions are not met (e.g., high speed, large object, rough shape), turbulent flow occurs and Stokes’ Law becomes invalid.
Temperature Dependence of Viscosity
Viscosity decreases with increasing temperature for liquids.
- Higher temperature → molecules move more easily → fluid becomes “thinner”.
- Example: Honey flows more easily when warm.
Viscosity increases with increasing temperature for gases.
- Higher temperature → more molecular momentum transfer → gas becomes “thicker”.
- Since Stokes’ Law involves \( \eta \), drag force is temperature dependent:
Higher temperature (liquid) → Lower \( \eta \) → Lower drag force.
When is Stokes’ Law Used?
- Falling droplets (rain, mist, spray).
- Oil droplets in Millikan’s experiment.
- Spherical particles settling in water or air.
- Measuring viscosity of fluids.
Example (Easy)
A sphere of radius \( 0.002\, \mathrm{m} \) moves at \( 0.05\, \mathrm{m\,s^{-1}} \) through oil of viscosity \( 0.9\, \mathrm{Pa\,s} \). Calculate the drag force.
▶️ Answer / Explanation
\( F = 6\pi \eta r v \)
\( = 6\pi (0.9)(0.002)(0.05) \approx 0.0017\, \mathrm{N} \)
Example (Medium)
A small metal ball of radius \( 0.004\, \mathrm{m} \) falls through glycerine at constant terminal velocity \( 0.20\, \mathrm{m\,s^{-1}} \). If glycerine has viscosity \( 1.2\, \mathrm{Pa\,s} \), find the drag force acting on the ball.
▶️ Answer / Explanation
\( F = 6\pi (1.2)(0.004)(0.20) = 0.0181\, \mathrm{N} \)
At terminal velocity, drag = weight – upthrust.
Example (Hard)
A sphere of radius \( 1.0 \times 10^{-3}\, \mathrm{m} \) falls through a liquid of density \( 900\, \mathrm{kg\,m^{-3}} \) and viscosity \( 0.85\, \mathrm{Pa\,s} \). The density of the sphere is \( 7800\, \mathrm{kg\,m^{-3}} \). Assuming it quickly reaches terminal velocity, find that velocity.
▶️ Answer / Explanation
At terminal velocity:
Weight – Upthrust = Drag
Weight of sphere:
\( W = \rho_s V g = 7800 \left(\dfrac{4}{3}\pi r^3\right) g \)
Upthrust:
\( U = \rho_f V g = 900 \left(\dfrac{4}{3}\pi r^3\right) g \)
Net downward force:
\( F_{\text{net}} = (\rho_s – \rho_f)\left(\dfrac{4}{3}\pi r^3\right) g \)
Set equal to drag \( 6\pi \eta r v \):
\( 6\pi \eta r v = (\rho_s – \rho_f)\left(\dfrac{4}{3}\pi r^3\right) g \)
Simplify and solve for \( v \):
\( v = \dfrac{2 r^2 g (\rho_s – \rho_f)}{9 \eta} \)
Substitute values:
\( v = \dfrac{2 (1\times10^{-3})^2 (9.8)(7800 – 900)}{9(0.85)} \approx 0.21\, \mathrm{m\,s^{-1}} \)
Terminal velocity ≈ \( 0.21\, \mathrm{m\,s^{-1}} \)
